矩阵求逆c++实现

2020-11-27 18:26

阅读：678

标签：c++ 逆矩阵 vc 数学学习

高斯消元法可以用来找出一个可逆矩阵的逆矩阵。设A 为一个N * N的矩阵，其逆矩阵可被两个分块矩阵表示出来。将一个N * N单位矩阵放在A 的右手边，形成一个N * 2N的分块矩阵B = [A,I] 。经过高斯消元法的计算程序后，矩阵B 的左手边会变成一个单位矩阵I ，而逆矩阵A ^(-1) 会出现在B 的右手边。假如高斯消元法不能将A 化为三角形的格式，那就代表A 是一个不可逆的矩阵。应用上，高斯消元法极少被用来求出逆矩阵。高斯消元法通常只为线性方程组求解。

 //********************************
//*** 求任何一个实矩阵的逆***
//********************************
#include "stdafx.h"
#include 
#include 
#include  
#include 
using namespace std; 
#define  N  10                //定义方阵的最大阶数为10
//函数的声明部分
float MatDet(float *p, int n);                    //求矩阵的行列式
float Creat_M(float *p, int m, int n, int k);    //求矩阵元素A(m, n)的代数余之式
void print(float *p, int n);                    //输出矩阵n*n
bool Gauss(float A[][N], float B[][N], int n);    //采用部分主元的高斯消去法求方阵A的逆矩阵B
int main()
{
    float *buffer, *p;            //定义数组首地址指针变量
    int row, num;                //定义矩阵的行数和矩阵元素个数
    int i, j;
    float determ;                //定义矩阵的行列式
    float a[N][N], b[N][N];
    int n;
    cout > row;
    num = 2 * row * row;
    buffer = (float *)calloc(num, sizeof(float));        //分配内存单元
    p = buffer;
    if (NULL != p)
    {
        for (i = 0; i > *p++;
            }
        }
    }
    else
    {
        cout > n;
    cout > a[i][j];
        }
    }
    //运用高斯消去法求该矩阵的逆矩阵并输出
    if (Gauss(a, b, n))
    {
        cout  fabs(max))
            {
                max = t[j][i];
                k = j;
            }
        }
        //如果主元所在行不是第i行，进行行交换
        if (k != i)
        {
            for (j = 0; j 第n行
        {
            if (j != i)                //不是第i行
            {
                temp = t[j][i];
                for (k = 0; k 实验结果：

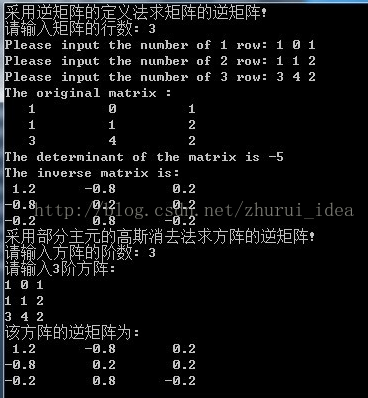
矩阵求逆c++实现,搜素材,soscw.com
矩阵求逆c++实现
标签：c++   逆矩阵   vc   数学   学习   
原文地址：http://blog.csdn.net/zhurui_idea/article/details/24864155