Gym 101986D Making Perimeter of the Convex Hull Shortest（凸包+极角排序）

2020-12-13 16:57

阅读：562

标签：向量 ide test order space cond target bit fun

首先肯定是构造一个完整的凸包包括所有的点，那么要使得刚好有两个点在外面，满足这个条件的只有三种情况。

1.两个在凸包上但是不连续的两个点。

2.两个在凸包上但是连续的两个点。

3.一个在凸包上，还有一个在这个点去掉后这段新凸包边上的一个点。

如何快速的截取新凸包的点是谁呢，我们可以将整个凸包划分区域，每个点删掉后，只可能在这块区域内选择新的点。那么我们就可以随机在凸包内部选择一个点，我使用的是凸包的重心作为坐标原点o，那么整个凸包移到原点处，然后在这个点的左侧和右侧的三角形区域内才是有可能构成新凸包边上的点，那我们只需要暴力枚举这部分内的点重构这条凸包边。那么第一第二种情况可以通过这个处理，第三种情况其实就是第一种情况套了第一种情况，那么就限暴力处理第一种情况的新凸包边，再在新凸包上继续分割三角区域，最后重构新凸包边中的新凸包边。

极角排序的时候细节处理有点坑，注意选择区域范围的角度相对大小，大型模拟题.... or

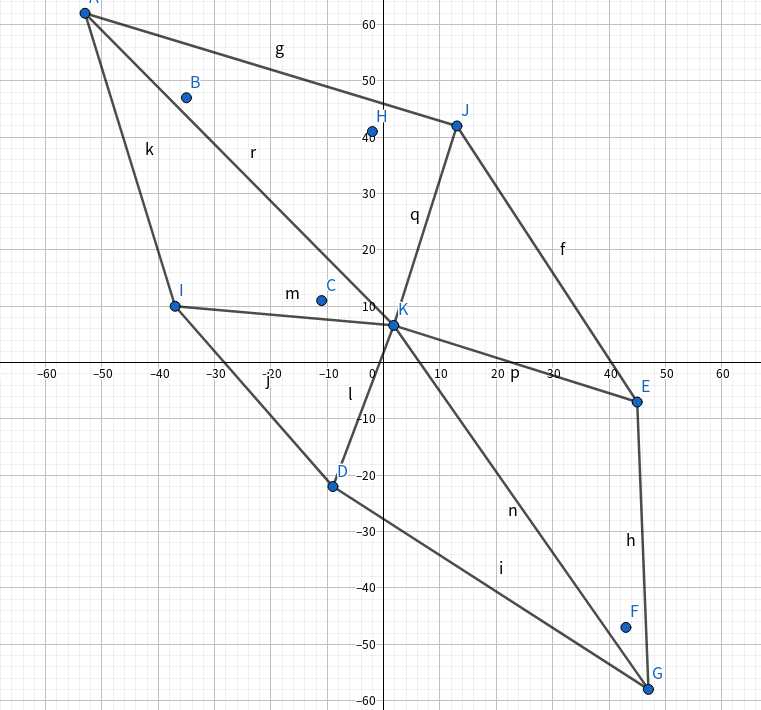
k点为重心

  1 //      ——By DD_BOND
  2 
  3 //#include  4 //#include  5 //#include
  6 #include  7 #include
  8 #include  9 //#include
 10 #include 11 #include 12 #include 13 #include 14 #include 15 #include 16 #include 17 #include 18 #include 19 #includestring>
 20 #include 21 #include 22 #include 23 #include 24 #include 25 #include 26 #includeset>
 27 
 28 #define fi first
 29 #define se second
 30 #define pb push_back
 31 #define MP make_pair
 32 
 33 #pragma GCC optimize(3)
 34 #pragma GCC target("sse,sse2,sse3,ssse3,sse4,popcnt,abm,mmx,avx,tune=native")
 35 
 36 using namespace std;
 37 
 38 typedef long double db;
 39 typedef long long ll;
 40 typedef pair Pd;
 41 typedef pairint,int> P;
 42 typedef pair Pll;
 43 
 44 const db eps=1e-8;
 45 const int MAXN=1e6+10;
 46 const db pi=acos(-1.0);
 47 const ll INF=0x3f3f3f3f3f3f3f3f;
 48 
 49 inline int dcmp(db x){
 50     if(fabs(x)return 0;
 51     return (x>0? 1: -1);
 52 }
 53 
 54 inline db Sqrt(db x){
 55     return x>0? sqrt(x): 0;
 56 }
 57 
 58 inline db sqr(db x){ return x*x; }
 59 
 60 struct Point{
 61     db x,y,ang;
 62     Point(){ x=0,y=0; }
 63     Point(db _x,db _y):x(_x),y(_y){}
 64     void input(){
 65         double _x,_y;
 66         scanf("%lf%lf",&_x,&_y);
 67         x=_x,y=_y;
 68     }
 69     bool operator ==(const Point &b)const{
 70         return (dcmp(x-b.x)==0&&dcmp(y-b.y)==0);
 71     }
 72     bool operator !=(const Point &b)const{
 73         return !((dcmp(x-b.x)==0&&dcmp(y-b.y)==0));
 74     }
 75     bool operator const Point &b)const{
 76         return (dcmp(x-b.x)==0? dcmp(y-b.y)0 : xb.x);
 77     }
 78     Point operator +(const Point &b)const{
 79         return Point(x+b.x,y+b.y);
 80     }
 81     Point operator -(const Point &b)const{
 82         return Point(x-b.x,y-b.y);
 83     }
 84     Point operator *(db a){
 85         return Point(x*a,y*a);
 86     }
 87     Point operator /(db a){
 88         return Point(x/a,y/a);
 89     }
 90     db len2(){  //长度平方
 91         return sqr(x)+sqr(y);
 92     }
 93     db len(){   //长度
 94         return Sqrt(len2());
 95     }
 96     db polar(){ //向量的极角
 97         return atan2(y,x);   //返回与x轴正向夹角(-pi~pi]
 98     }
 99 };
100 
101 inline db cross(Point a,Point b){   //叉积
102     return a.x*b.y-a.y*b.x;
103 }
104 
105 inline db dot(Point a,Point b){ //点积
106     return a.x*b.x+a.y*b.y;
107 }
108 
109 inline db dis(Point a,Point b){ //两点的距离
110     Point p=b-a;    return p.len();
111 }
112 
113 Point centre_of_polygon(Point *p,int n){    //三角形重心加面积权值的平均求多边形的重心
114     db sum=0,sumx=0,sumy=0;
115     Point p1=p[0],p2=p[1],p3;
116     for(int i=2;i){
117         p3=p[i];
118         db area=cross(p2-p1,p3-p2)/2;
119         sum+=area;
120         sumx+=(p1.x+p2.x+p3.x)*area;
121         sumy+=(p1.y+p2.y+p3.y)*area;
122         p2=p3;
123     }
124     return Point(sumx/(3*sum),sumy/(3*sum));
125 }
126 
127 Point tmp[MAXN],ins[MAXN];
128 
129 int convex_hull(Point *p,int n,Point *ch){  //求凸包
130     int m=0;
131     sort(p,p+n);
132     for(int i=0;i){
133         while(m>1&&dcmp(cross(tmp[m-1]-tmp[m-2],p[i]-tmp[m-1]))0) m--;
134         tmp[m++]=p[i];
135     }
136     int k=m;
137     for(int i=n-2;i>=0;i--){
138         while(m>k&&dcmp(cross(tmp[m-1]-tmp[m-2],p[i]-tmp[m-1]))0) m--;
139         tmp[m++]=p[i];
140     }
141     if(n>1) m--;
142     for(int i=0;itmp[i];
143     return m;
144 }
145 
146 db ans;
147 pairint>rec[MAXN];
148 Point point[MAXN],convex[MAXN],o;
149 vectorside[MAXN],in[MAXN],st;
150 
151 bool cmp(Point a,Point b){
152     db dx=(a-o).polar(),dy=(b-o).polar();
153     if(dcmp(dx-dy)==0)  return dis(a,o)>dis(b,o);
154     return dxdy;
155 }
156 
157 int main(void){
158     int n,m;  scanf("%d",&n);
159     for(int i=0;i)    point[i].input();
160 
161     m=convex_hull(point,n,convex);
162     o=centre_of_polygon(convex,m);
163 
164     sort(point,point+n,cmp);
165     sort(convex,convex+m,cmp);
166 
167     for(int i=0;i){
168         point[i].ang=(point[i]-o).polar();
169         point[i+n]=point[i];
170         point[i+n].ang+=2*pi;
171     }
172     for(int i=0;i){
173         convex[i].ang=(convex[i]-o).polar();
174         convex[i+m]=convex[i];
175         convex[i+m].ang+=2*pi;
176     }
177 
178     for(int i=0,j=0;i){
179         while(dcmp(convex[i].ang-point[j].ang)>0)   j++;
180         while(dcmp(point[j].ang-convex[i+1].ang)0){
181             if(point[j]!=convex[i]) side[i].pb(point[j]);
182             j++;
183         }
184     }
185 
186     // a point on convex
187     for(int i=0;i){
188         int l=(i==0? m-1: i-1),p=0;
189         tmp[p++]=convex[l];
190         for(int j=0;j){
191             while(p>1&&dcmp(cross(tmp[p-1]-tmp[p-2],side[l][j]-tmp[p-1]))0)    p--;
192             tmp[p++]=side[l][j];
193         }
194         for(int j=0;j){
195             while(p>1&&dcmp(cross(tmp[p-1]-tmp[p-2],side[i][j]-tmp[p-1]))0)    p--;
196             tmp[p++]=side[i][j];
197         }
198         while(p>1&&dcmp(cross(tmp[p-1]-tmp[p-2],convex[i+1]-tmp[p-1]))0)    p--;
199         tmp[p++]=convex[i+1];
200 
201         db sum=dis(convex[l],convex[i])+dis(convex[i],convex[i+1]);
202         for(int j=0;j1;j++)  sum-=dis(tmp[j],tmp[j+1]);
203         rec[i]=MP(sum,i);
204     }
205     sort(rec,rec+m,greaterint> >());
206     if(abs(rec[0].se-rec[1].se)!=1&&abs(rec[0].se-rec[1].se)!=m-1)  ans=max(ans,rec[0].fi+rec[1].fi);
207     if(abs(rec[0].se-rec[2].se)!=1&&abs(rec[0].se-rec[2].se)!=m-1)  ans=max(ans,rec[0].fi+rec[2].fi);
208     if(abs(rec[1].se-rec[2].se)!=1&&abs(rec[1].se-rec[2].se)!=m-1)  ans=max(ans,rec[1].fi+rec[2].fi);
209 
210     // two consecutive point on convex
211     for(int i=0;i){
212         int l=(i==0? m-1: i-1),p=0;
213         tmp[p++]=convex[l];
214         for(int j=0;j){
215             while(p>1&&dcmp(cross(tmp[p-1]-tmp[p-2],side[l][j]-tmp[p-1]))0)    p--;
216             tmp[p++]=side[l][j];
217         }
218         for(int j=0;j){
219             while(p>1&&dcmp(cross(tmp[p-1]-tmp[p-2],side[i][j]-tmp[p-1]))0)    p--;
220             tmp[p++]=side[i][j];
221         }
222         for(int j=0;j1)%m].size();j++){
223             while(p>1&&dcmp(cross(tmp[p-1]-tmp[p-2],side[(i+1)%m][j]-tmp[p-1]))0)    p--;
224             tmp[p++]=side[(i+1)%m][j];
225         }
226         while(p>1&&dcmp(cross(tmp[p-1]-tmp[p-2],convex[i+2]-tmp[p-1]))0)    p--;
227         tmp[p++]=convex[i+2];
228 
229         db sum=dis(convex[l],convex[i])+dis(convex[i],convex[i+1])+dis(convex[i+1],convex[i+2]);
230         for(int j=0;j1;j++)  sum-=dis(tmp[j],tmp[j+1]);
231         ans=max(ans,sum);
232     }
233 
234     // a point on convex and a point inside convex
235     for(int i=0;i){
236         int l=(i==0? m-1: i-1),p=0;
237         tmp[p++]=convex[l];
238         if(i==0)    tmp[p-1].ang-=2*pi;
239         for(int j=0;j){
240             st.pb(side[l][j]);
241             if(i==0)    st.back().ang-=2*pi;
242             while(p>1&&dcmp(cross(tmp[p-1]-tmp[p-2],side[l][j]-tmp[p-1]))0)    p--;
243             tmp[p++]=side[l][j];
244         }
245         for(int j=0;j){
246             st.pb(side[i][j]);
247             while(p>1&&dcmp(cross(tmp[p-1]-tmp[p-2],side[i][j]-tmp[p-1]))0)    p--;
248             tmp[p++]=side[i][j];
249         }
250         while(p>1&&dcmp(cross(tmp[p-1]-tmp[p-2],convex[i+1]-tmp[p-1]))0)    p--;
251         tmp[p++]=convex[i+1];
252 
253         for(int j=0,k=0;j1;j++){
254             while(k0)   k++;
255             while(k1].ang)0){
256                 if(tmp[j]!=st[k])   in[j].pb(st[k]);
257                 k++;
258             }
259         }
260         db sum=dis(convex[l],convex[i])+dis(convex[i],convex[i+1]);
261         for(int j=0;j1;j++)  sum-=dis(tmp[j],tmp[j+1]);
262         for(int j=1;j1;j++){
263             int t=0;
264             ins[t++]=tmp[j-1];
265             for(int k=0;kin[j-1].size();k++){
266                 while(t>1&&dcmp(cross(ins[t-1]-ins[t-2],in[j-1][k]-ins[t-1]))0)    t--;
267                 ins[t++]=in[j-1][k];
268             }
269             for(int k=0;kin[j].size();k++){
270                 while(t>1&&dcmp(cross(ins[t-1]-ins[t-2],in[j][k]-ins[t-1]))0)  t--;
271                 ins[t++]=in[j][k];
272             }
273             while(t>1&&dcmp(cross(ins[t-1]-ins[t-2],tmp[j+1]-ins[t-1]))0)  t--;
274             ins[t++]=tmp[j+1];
275 
276             db now=sum+dis(tmp[j-1],tmp[j])+dis(tmp[j],tmp[j+1]);
277             for(int k=0;k1;k++)  now-=dis(ins[k],ins[k+1]);
278             ans=max(ans,now);
279         }
280         st.clear();
281         for(int j=0;jin[j].clear();
282     }
283     printf("%.12f\n",(double)ans);
284     return 0;
285 }

Gym 101986D Making Perimeter of the Convex Hull Shortest（凸包+极角排序）

标签：向量 ide test order space cond target bit fun

原文地址：https://www.cnblogs.com/dd-bond/p/11622216.html

上一篇：pycharm使用运行环境显示的是python console

下一篇：python进阶二（模块）【2-1 python之导入模块】

文章来自：搜素材网的编程语言模块，转载请注明文章出处。
文章标题：Gym 101986D Making Perimeter of the Convex Hull Shortest（凸包+极角排序）
文章链接：http://soscw.com/index.php/essay/36615.html

亲，登录后才可以留言！

Gym 101986D Making Perimeter of the Convex Hull Shortest（凸包+极角排序）

评论

热门文章

推荐文章

最新文章

置顶文章