《数据结构与算法之美》28——动态规划理论
2020-12-18 16:36
标签:文章 二层 推导 表示 不同 总结 说明 适合 tps 上一节通过两个经理案例初步认识动态规划,今天这一节主要讲动态规划的理论知识。 实际上,动态规划作为一个非常成熟的算法思想,这部分理论总结为“一个模型三个特征”。 一个模型指动态规划适合解决的问题模型。这个模型定义为“多阶段决策最优解模型”。 一般是用动态规划来解决最优问题。而解决问题的过程,需要经历多个决策阶段。每个决策阶段都对应着一组状态。然后寻找一组决策序列,经过这组决策序列,能够产生最终期望求解的值。 三个特征分别是:最优子结构、无后效性和重复子问题。 解决动态规划问题,一般有两种思路。分别是状态转移表法和状态转移方程法。 状态转移表法的解题思路概括为:回溯算法实现-定义状态-画递归树-找重复子问题-画状态转移表-根据递推关系填表-将填表过程翻译成代码。 我们来看一下,如何套用状态转移表法来解决动态规划问题。 假设我们有一个n乘以n的矩阵w[n][n]。矩阵存储的都是正整数。棋子起始位置在左上角,终止位置在右下角。那从左上角移动到右下角的最短路径长度是多少? 从回溯代码的函数调用可知,每一个状态包含三个变量(i, j, dist),其中 i,j 分别表示行和列,dist 表示从起点到达(i, j)的路径长度。 有了回溯代码和状态定义,把每个状态作为一个节点,画出递归树。 从上图可知,存在重复子问题。 我们画出一个二维状态表,表中的行、列表示棋子所在的位置,表中的数值表示从起点到这个位置的最短路径。 按照决策过程,通过不断状态递推演进,将状态表填好。 状态转移方程法的解题思路概括为:找最优子结构-写状态转移方程-将状态转移方程翻译成代码。 还是拿上面的例子来说明。 min_dist(i, j)可以通过min_dist(i, j-1)和min_dist(i-1, j)两个状态推导出来,符合“最优子结构”。 min_dist(i, j) = w[i][j] + min(min_dist(i, j-1), min_dist(i-1, j)) 强调一下,状态转移方程是解决动态规划的关键。 一般情况下,有两种代码实现方法: 用递归+“备忘录”将状态转移方程翻译成代码。 动态规划有两种解题思路:状态转移表法和状态转移方程法。 状态转移表法的解题思路概括为:回溯算法实现-定义状态-画递归树-找重复子问题-画状态转移表-根据递推关系填表-将填表过程翻译成代码。 状态转移方程法的解题思路概括为:找最优子结构-写状态转移方程-将状态转移方程翻译成代码。 《数据结构与算法之美》28——动态规划理论 标签:文章 二层 推导 表示 不同 总结 说明 适合 tps 原文地址:https://www.cnblogs.com/liang24/p/13384809.html前言
“一个模型三个特征”理论讲解
一个模型
三个特征
两种动态规划解题思路总结
状态转移表法
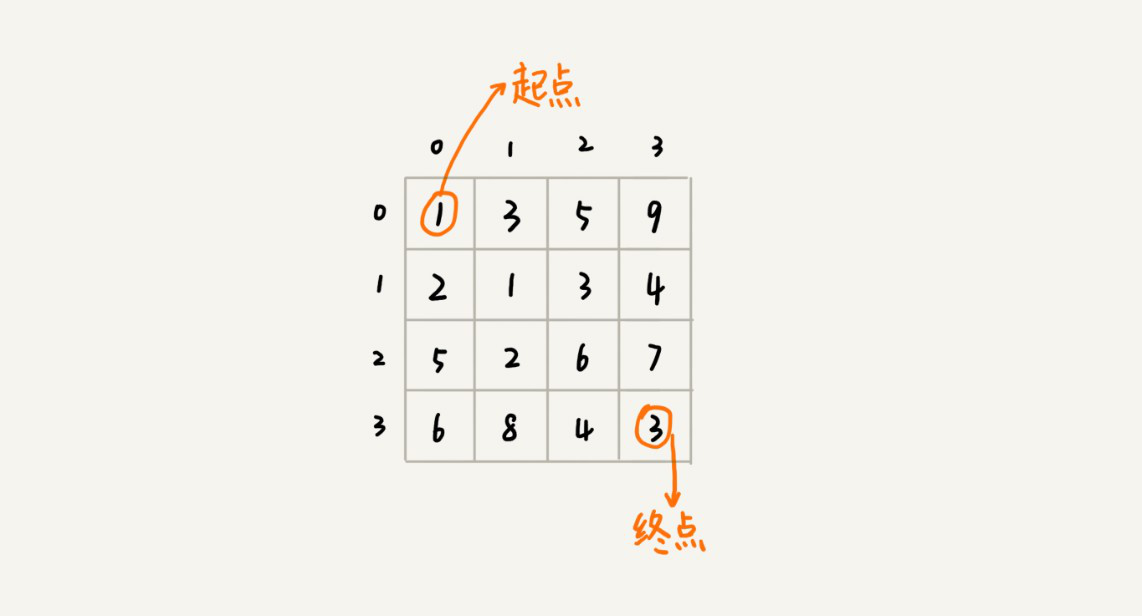
回溯算法实现
public class Solution {
private int minDist = int.MaxValue;
public int MinDist { get { return minDist; } }
// 调用方式:MinDistBT(0, 0, 0, w, n);
public void MinDistBT (int i, int j, int dist, int[][] w, int n) {
// 到达n-1, n-1这个位置了
if (i == n - 1 && j == n - 1) {
dist = dist + w[i][j];
if (dist 定义状态
画递归树
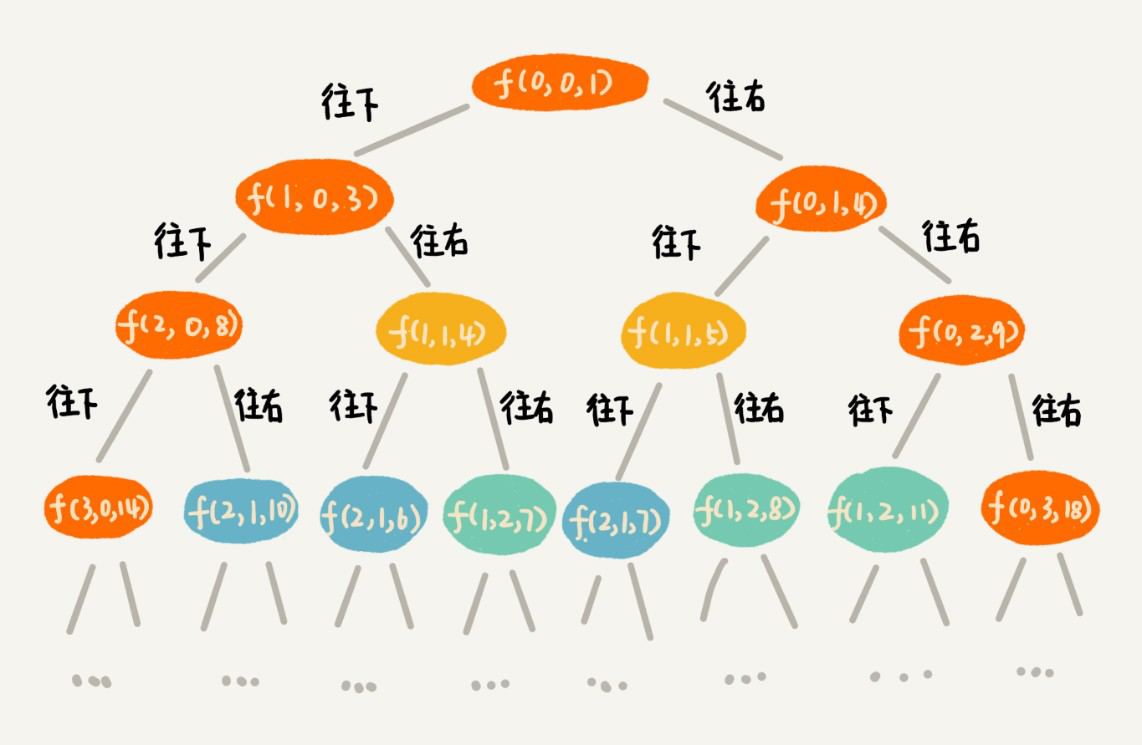
找重复子问题
画状态转移表
根据递推关系填表
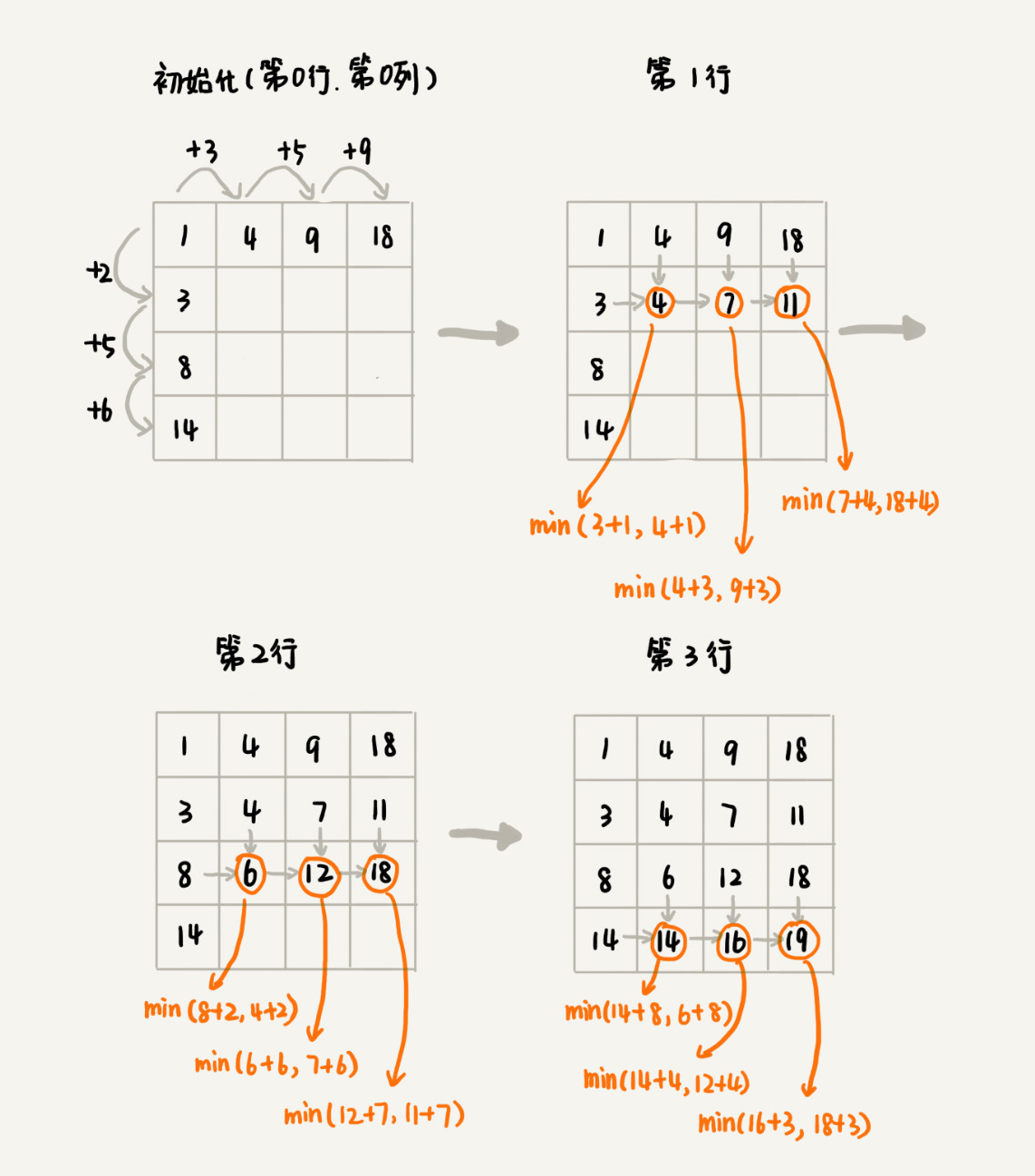
将填表过程翻译成代码
public class Solution2 {
public int MinDistDP (int[][] matrix, int n) {
int[][] states = new int[n][];
for (int i = 0; i 状态转移方程法
找最优子结构
写状态转移方程
将状态转移方程翻译成代码
public class Solution3 {
private int[, ] matrix = new int[4, 4] { { 1, 3, 5, 9 }, { 2, 1, 3, 4 }, { 5, 2, 6, 7 }, { 6, 8, 4, 3 } };
private int n = 4;
private int[, ] mem = new int[4, 4];
public int MinDist (int i, int j) { // 调用MinDist(n-1, n-1)
if (i == 0 && j == 0) return matrix[0, 0];
if (mem[i, j] > 0) return mem[i, j];
int minLeft = int.MaxValue;
if (j - 1 >= 0) {
minLeft = MinDist (i, j - 1);
}
int minUp = int.MaxValue;
if (i - 1 >= 0) {
minUp = MinDist (i - 1, j);
}
int curMinDist = matrix[i, j] + Math.Min (minLeft, minUp);
mem[i, j] = curMinDist;
return curMinDist;
}
}
总结
参考资料
下一篇:Python之面向对象
文章标题:《数据结构与算法之美》28——动态规划理论
文章链接:http://soscw.com/index.php/essay/37129.html