标签:需要 a算法 实现 三次 相同 个数 选择 动态规划 inf
Dijkstra也叫迪杰斯特拉,是典型最短路径算法,计算一个起始节点到路径中其他所有节点的最短路径的算法和思想。在一些专业课程中如数据结构,图论,运筹学等都有介绍。其思想是一种基础的求最短路径的算法,通过基础思想的变化可以解决很多复杂问题,如导航线路,动态规划等。
1|0Dijkstra 算法思想介绍
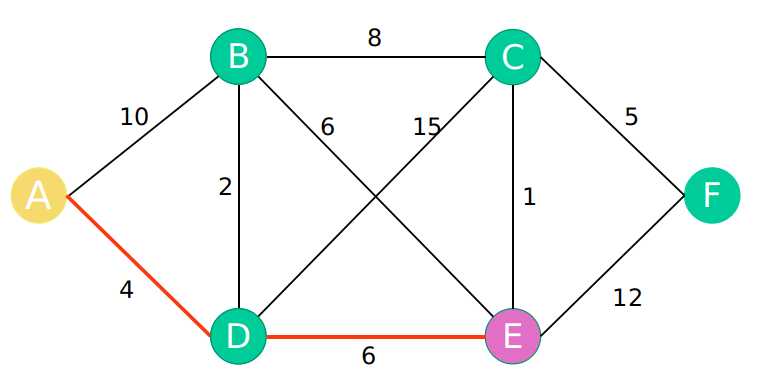
如下图是一个多节点,多路径图。下面以该图为例子讲解dijkstra算法寻找最短路径的过程。
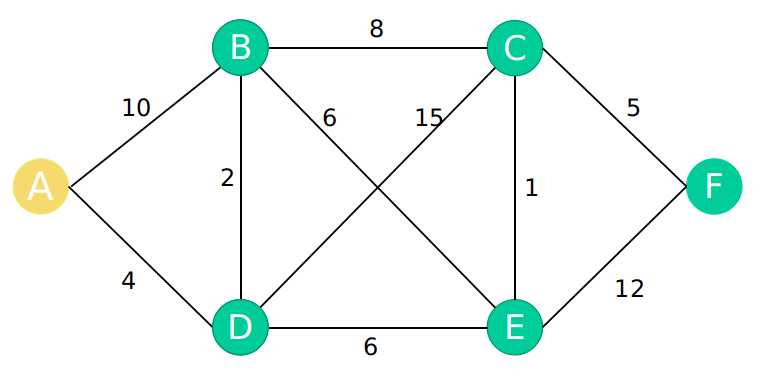
以A点为起始点,求A点到其他点 B C D E F 5个点的最短路径,最后得出A到其他点的最短路径。
因为要求A到其他5个点的最短距离,所以构造一个数组记录A到B C D E F 5个点的路径距离。约定:
- 如果A能够直接达到节点,则使用路径长度即权值作为其距离
- 如果A节点不能直接达到节点则使用无穷大表示A到该点距离。
- 任何点到自身都为0
那么在最开始时,A点到图中所有点的距离数组如下:
| A |
B |
C |
D |
E |
F |
| 0 |
10 |
无穷大 |
4 |
无穷大 |
无穷大 |
dijkstra的算法思想是从以上最短距离数组中每次选择一个最近的点,将其作为下一个点,然后重新计算从起始点经过该点到其他所有点的距离,更新最短距离数据。已经选取过的点就是确定了最短路径的点,不再参与下一次计算。

可能看到这里你完全不明白dijkstra算法的思想,心里可能想:这是说的人话吗?不要紧,如果算法一句话就能解释清楚,那就不会出现那么多算法书了。下面我们就从实际的选取过程中理解这个思想的精髓。
1|1第一次选取
构建好的数组是这样的:
| A |
B |
C |
D |
E |
F |
| 0 |
10 |
无穷大 |
4 |
无穷大 |
无穷大 |
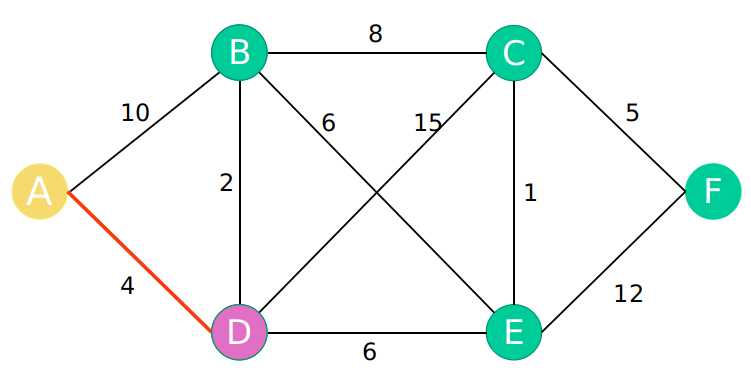
第一步选取该最短路径数组中值最小的一个点。因为A点到本身不需要参与运算,所以从剩下的点中选择最短的一个是D。
第二步以A-D的距离为最近距离更新A点到所有点的距离。即相当于A点经过D点,计算A到其他点的距离。
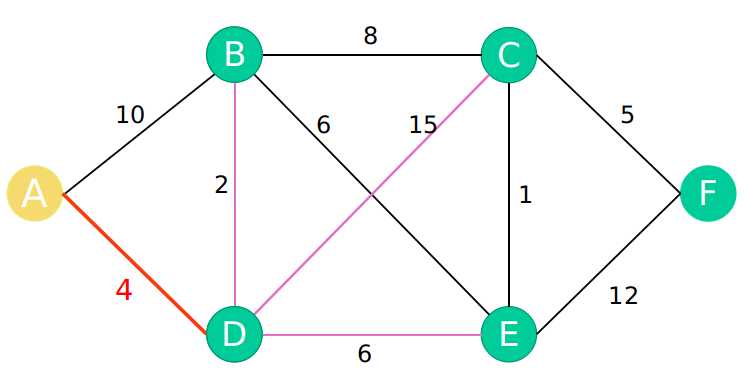
A-A : 0
A-B : A-D-B:6
A-C : A-D-C:19
A-D : A-D:4
A-E : A-D-E:10
A-F : A-D-F:去穷大
| A |
B |
C |
D |
E |
F |
| 0 |
6 |
19 |
4 |
10 |
无穷大 |
将现在A到各个点的距离和之前的比较,到相同点取最小值。更新了B C E的距离,得到如下新的最短距离数组:
| A |
B |
C |
D |
E |
F |
| 0 |
6 |
19 |
4 |
10 |
无穷大 |
同时现在A D两点已经计算过,不参与下面的计算。
1|2第二次选取
第二次选取的数组为第一次中更新过最短距离的数组
| A |
B |
C |
D |
E |
F |
| 0 |
6 |
19 |
4 |
10 |
无穷大 |
第一步:因为A D 不参与选取,所有从剩下的点中选取最近距离是点B
第二步:以B为最新点,更新最短数组
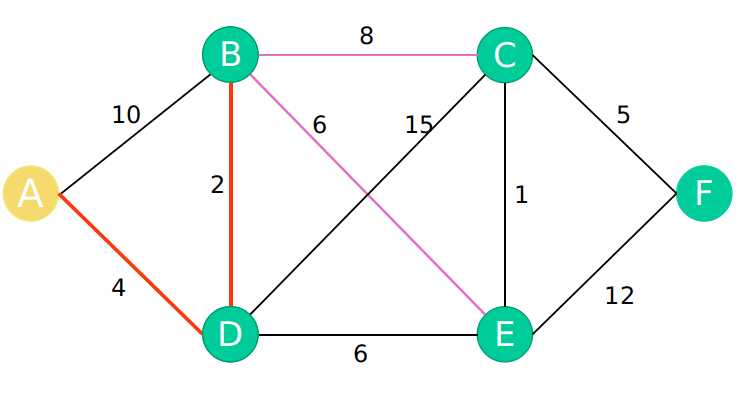
A-A : 0
A-B : A-D-B:6
A-C : A-D-B-C:14
A-D : A-D:4
A-E : A-D-B-E:12
A-F : A-D-B-F:无穷大
| A |
B |
C |
D |
E |
F |
| 0 |
6 |
14 |
4 |
12 |
无穷大 |
对比现在的最短距离和上一个数组的距离,到相同节点取最小的,C点由19更新成14,E点走A-D-E为10,距离更短所以不更新(敲黑板,这个重要),得到如下数组:
| A |
B |
C |
D |
E |
F |
| 0 |
6 |
14 |
4 |
10 |
无穷大 |
此时B点加入最短路径范围中。
1|3第三次选取
上一步得到的数组为:
| A |
B |
C |
D |
E |
F |
| 0 |
6 |
14 |
4 |
10 |
无穷大 |
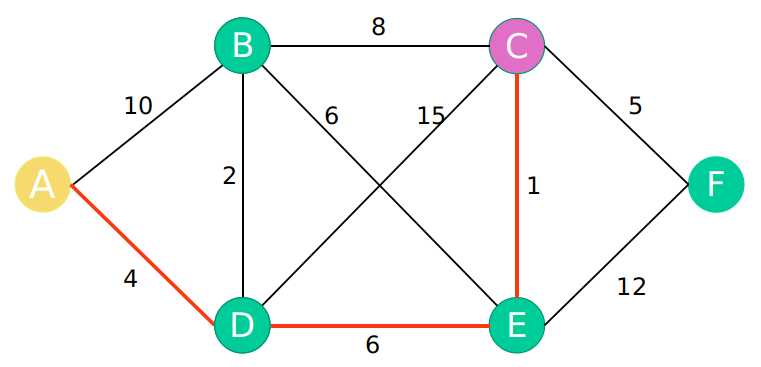
第一步:选取除了A B D节点之外的剩余节点中最短节点,为点E
第二步:以E点为最新节点,更新最短路径数组
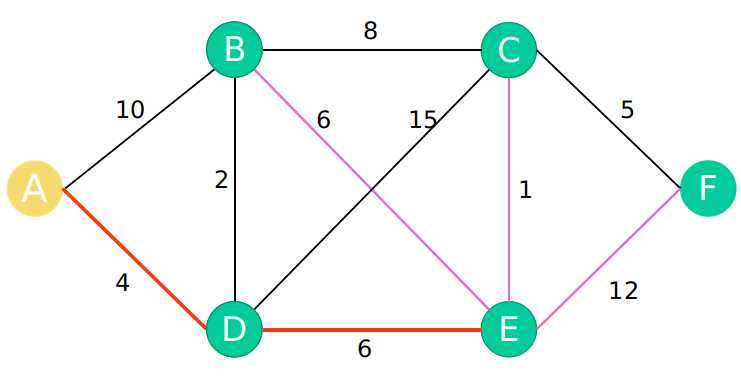
因为在上一部中计算达到E点的距离时没有更新距离,A-D-E 为10 最短,所以更新E点到B C F点的距离时走的路径是A-D-E。注意这里的最短距离有对应的路径,选择最小值就是选择最短距离。
A-A : 0
A-B : A-D-B:6
A-C : A-D-E-C:11
A-D : A-D:4
A-E : A-D-E:10
A-F : A-D-E-F:22
| A |
B |
C |
D |
E |
F |
| 0 |
6 |
11 |
4 |
10 |
22 |
对比现在的最短距离和上一个数组的距离,到相同节点取最小的,更新C点走A-D-E-C 为11,比之前的A-D-B-C14距离更近,更新到F点距离,得到如下数组:
| A |
B |
C |
D |
E |
F |
| 0 |
6 |
11 |
4 |
10 |
22 |
此时E点加入最短路径范围中。
1|4第四次选取
| A |
B |
C |
D |
E |
F |
| 0 |
6 |
11 |
4 |
10 |
22 |
第一步:选取除了A B D E节点之外的剩余节点中最短节点,为点C
第二步:以C点为最新节点,更新最短路径数组
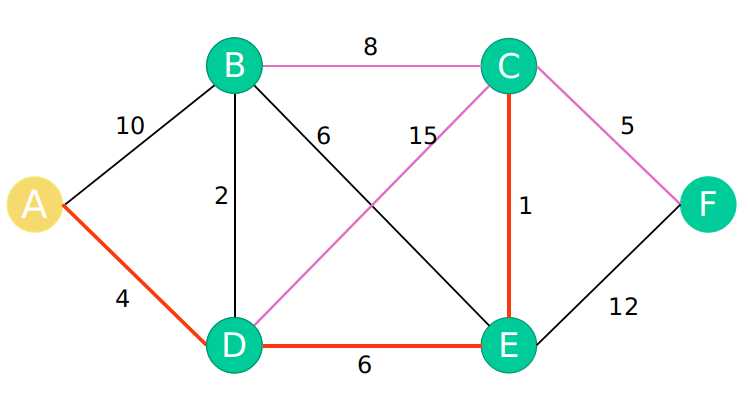
A-A : 0
A-B : A-D-B:6
A-C : A-D-E-C:11
A-D : 4
A-E : A-D-E:10
A-F : A-D-E-C-F:16
| A |
B |
C |
D |
E |
F |
| 0 |
6 |
11 |
4 |
10 |
16 |
对比现在的最短距离和上一个数组的距离,到相同节点取最小的,更新到F点距离,可以得到如下数组:
| A |
B |
C |
D |
E |
F |
| 0 |
6 |
11 |
4 |
10 |
16 |
1|5第五次选取
| A |
B |
C |
D |
E |
F |
| 0 |
6 |
11 |
4 |
10 |
16 |
第一步:选取除了A B C D E节点之外的剩余节点中最短节点,也就是最后一个节点:F
第二步:以F点为最新节点,更新最短路径数组。由于F点是最后一个点,所以也不用更新数组,目前的数组就是所求数组
将F点加入最短路径范围中,此时所有的点都加入了最短路径范围,也就是说A点到所有点的距离都找到了。最总得出的距离值为:
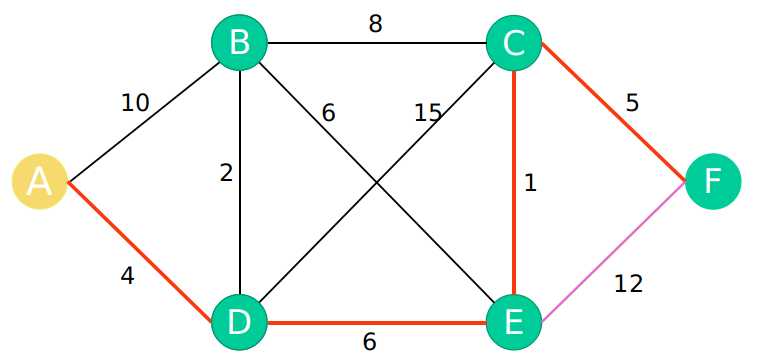
最终得到的结果为:
| A |
B |
C |
D |
E |
F |
| 0 |
6 |
11 |
4 |
10 |
16 |
1|6最终结果
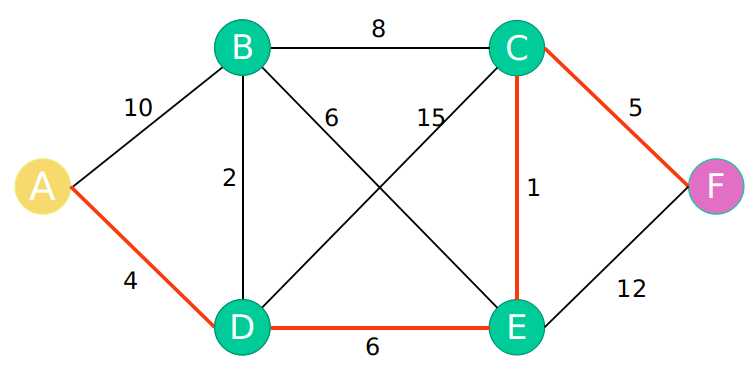
相应的A点到所有点的最短路径走法最终得到的结果为:
| A |
B |
C |
D |
E |
F |
| 0 |
6 |
11 |
4 |
10 |
16 |
A-A:0
A-B : A-D-B:6

A-C : A-D-E-C:11
A-D:4
A-E:A-D-E:10
A-F:A-D-E-C-F:16
1|7算法总结
Dijkstra算法作为求最短路径的经典算法,个人理解为算法提供了一种思想,每走一步都是找到最短的路径,并且每走一步都实时更新所有距离,保证每次都选择最短路径。
2|0python实现Dijkstra
将以上的过程使用python来实现。
首先总结一个Dijkstra算法的核心思想,分成两步走:
- 构造一个最短路径数组,每次找到数组中未访问的节点里最小的点
- 以上一步的节点为最新节点,更新起始点到所有点的距离
使用python就是实现这两步即可
一篇文章讲透Dijkstra最短路径算法-内有PHP-juepe运作缓存解答
标签:需要 a算法 实现 三次 相同 个数 选择 动态规划 inf
原文地址:https://www.cnblogs.com/fjj-1515/p/13030422.html











