k-means聚类分析 python 代码实现(不使用现成聚类库)
2020-12-29 07:28
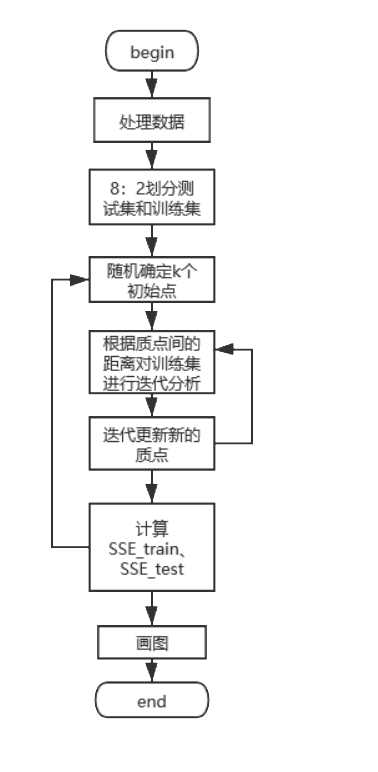
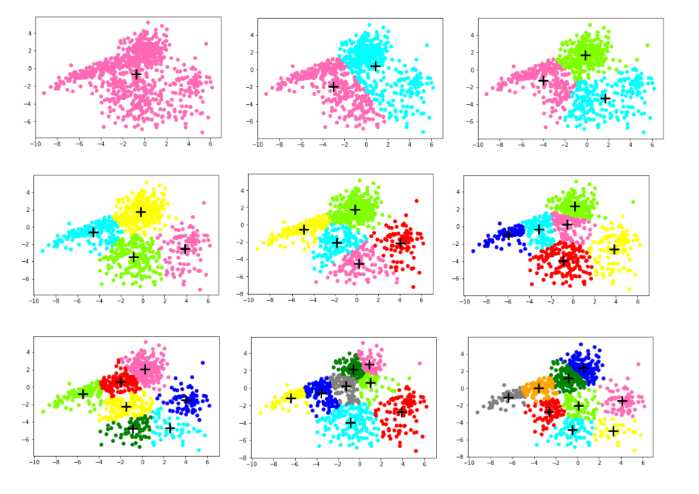
标签:RKE show 个数 lin rand lib 小白 pytho 博客 1、使用 K-means 模型进行聚类,尝试使用不同的类别个数 K,并分析聚类结果。 首先确定k,随机选择k个初始点之后所有点根据距离质点的距离进行聚类分析,离某一个质点a相较于其他质点最近的点分配到a的类中,根据每一类mean值更新迭代聚类中心,在迭代完成后分别计算训 练集和测试集的损失函数SSE_train、SSE_test,画图进行分析。 伪代码如下: 算法流程图: 可以看出SSE随着K的增长而减小,测试集和训练集的图形趋势几乎一致,在相同的K值下,测试集的SSE大于训练集的SSE。于是我对于在相同的K值下的SSE_test和SSE_train做了减法(上图3),可知K=4时数据得出结果最好。这里我主要使用肘部原则来判断。本篇并未实现轮廓系数,由于博主是python小白,故此次代码参考了一部分CSDN的博客:https://blog.csdn.net/qq_37509235/article/details/82925781 k-means聚类分析 python 代码实现(不使用现成聚类库) 标签:RKE show 个数 lin rand lib 小白 pytho 博客 原文地址:https://www.cnblogs.com/bestluna/p/12988361.html一、实验目标
二、算法原理
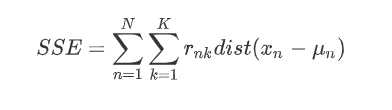
num=10 #k的种类
for k in range(1,num):
随机选择k个质点
for i in range(n): #迭代n次
根据点与质点间的距离对于X_train进行聚类
根据mean值迭代更新质点
计算SSE_train
计算SSE_test
画图
三、代码实现
1、导入库
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from sklearn.model_selection import train_test_split
2、计算距离
def distance(p1,p2):
return np.sqrt((p1[0]-p2[0])**2+(p1[1]-p2[1])**2)
3、计算均值
def means(arr):
return np.array([np.mean([p[0] for p in arr]),np.mean([p[1] for p in arr])])
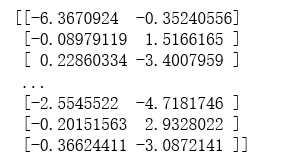
4、二维数据处理
#数据处理
data= pd.read_table(‘cluster.dat‘,sep=‘\t‘,header=None)
data.columns=[‘x‘]
data[‘y‘]=None
for i in range(len(data)): #遍历每一行
column = data[‘x‘][i].split( ) #分开第i行,x列的数据。split()默认是以空格等符号来分割,返回一个列表
data[‘x‘][i]=column[0] #分割形成的列表第一个数据给x列
data[‘y‘][i]=column[1] #分割形成的列表第二个数据给y列
list=[]
list1=[]
for i in range(len(data)):
list.append(float(data[‘x‘][i]))
list.append(float(data[‘y‘][i]))
list1.append(list)
list=[]
arr=np.array(list1)
print(arr)
5、划分数据集和训练集
#按照8:2划分数据集和训练集
X_train, X_test = train_test_split(arr,test_size=0.2,random_state=1)
6、主要聚类实现
count=10 #k的种类:1、2、3...10
SSE_train=[] #训练集的SSE
SSE_test=[] #测试集的SSE
n=20 #迭代次数
for k in range(1,count):
cla_arr=[] #聚类容器
centroid=[] #质点
for i in range(k):
j=np.random.randint(0,len(X_train))
centroid.append(list1[j])
cla_arr.append([])
centroids=np.array(centroid)
cla_tmp=cla_arr #临时训练集聚类容器
cla_tmp1=cla_arr #临时测试集聚类容器
for i in range(n): #开始迭代
for e in X_train: #对于训练集中的点进行聚类分析
pi=0
min_d=distance(e,centroids[pi])
for j in range(k):
if(distance(e,centroids[j])min_d):
min_d=distance(e,centroids[j])
pi=j
cla_tmp[pi].append(e) #添加点到相应的聚类容器中
for m in range(k):
if(n-1==i):
break
centroids[m]=means(cla_tmp[m])#迭代更新聚类中心
cla_tmp[m]=[]
dis=0
for i in range(k): #计算训练集的SSE_train
for j in range(len(cla_tmp[i])):
dis+=distance(centroids[i],cla_tmp[i][j])
SSE_train.append(dis)
col = [‘HotPink‘,‘Aqua‘,‘Chartreuse‘,‘yellow‘,‘red‘,‘blue‘,‘green‘,‘grey‘,‘orange‘] #画出对应K的散点图
for i in range(k):
plt.scatter([e[0] for e in cla_tmp[i]],[e[1] for e in cla_tmp[i]],color=col[i])
plt.scatter(centroids[i][0],centroids[i][1],linewidth=3,s=300,marker=‘+‘,color=‘black‘)
plt.show()
for e in X_test: #测试集根据训练集的质点进行聚类分析
ki=0
min_d=distance(e,centroids[ki])
for j in range(k):
if(distance(e,centroids[j])min_d):
min_d=distance(e,centroids[j])
ki=j
cla_tmp1[ki].append(e)
for i in range(k): #计算测试集的SSE_test
for j in range(len(cla_tmp1[i])):
dis+=distance(centroids[i],cla_tmp1[i][j])
SSE_test.append(dis)
7、画图
SSE=[] #计算测试集与训练集SSE的差值
for i in range(len(SSE_test)):
SSE.append(SSE_test[i]-SSE_train[i])
x=[1,2,3,4,5,6,7,8,9]
plt.figure()
plt.plot(x,SSE_train,marker=‘*‘)
plt.xlabel("K")
plt.ylabel("SSE_train")
plt.show() #画出SSE_train的图
plt.figure()
plt.plot(x,SSE_test,marker=‘*‘)
plt.xlabel("K")
plt.ylabel("SSE_test")
plt.show() #画出SSE_test的图
plt.figure()
plt.plot(x,SSE,marker=‘+‘)
plt.xlabel("K")
plt.ylabel("SSE_test-SSE_train")
plt.show() #画出SSE_test-SSE_train的图
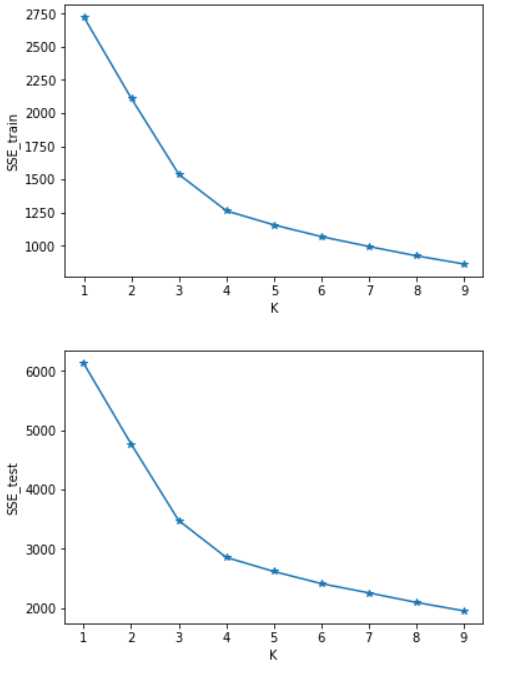
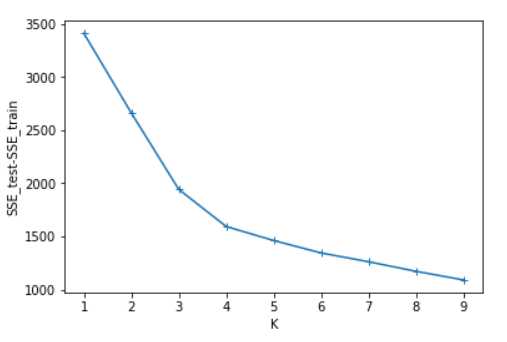
四、实验结果分析
文章标题:k-means聚类分析 python 代码实现(不使用现成聚类库)
文章链接:http://soscw.com/index.php/essay/39003.html