算法复杂度
2021-01-14 03:13
标签:问题 依次 应该 mamicode 常见 循环结构 渐进 一点 情况下 算法的时间复杂度反映了程序执行时间随输入规模增长而增长的量级,在很大程度上能很好反映出算法的优劣与否。算法执行时间需通过依据该算法编制的程序在计算机上运行时所消耗的时间来度量。而度量一个程序的执行时间通常有两种方法。 T (n) = Ο(f (n)) 表示存在一个常数C,使得在当n趋于正无穷时总有 T (n) ≤ C * f(n)。例如,O(2n2+n +1) = O (3n2+n+3) = O (7n2 + n) = O ( n2 ) 。注意到大O符号里隐藏着一个常数C,所以f(n)里一般不加系数。特殊的,当算法中语句执行次数为一个常数时,时间复杂度为O(1)。 另外,在时间频度不相同时,时间复杂度有可能相同,如T(n)=n2+3n+4与T(n)=4n2+2n+1它们的频度不同,但时间复杂度相同,都为O(n2)。 按数量级递增排列,常见的时间复杂度有: 随着问题规模n的不断增大,上述时间复杂度不断增大,算法的执行效率越低。 从图中可见,我们应该尽可能选用多项式阶O(nk)的算法,而不希望用指数阶的算法。 常见的算法时间复杂度由小到大依次为:Ο(1)<Ο(log2n)<Ο(n)<Ο(nlog2n)<Ο(n2)<Ο(n3)<…<Ο(2n)<Ο(n!) 具体步骤是: 如果算法中包含嵌套的循环,则基本语句通常是最内层的循环体,如果算法中包含并列的循环,则将并列循环的时间复杂度相加。 例如: 第一个for循环的时间复杂度为Ο(n),第二个for循环的时间复杂度为Ο(n2),则整个算法的时间复杂度为Ο(n+n2)=Ο(n2)。 另外还有以下2个运算法则 以上三条单个语句的频度均为1,该程序段的执行时间是一个与问题规模n无关的常数。算法的时间复杂度为常数阶,记作T(n)=O(1)。注意:如果算法的执行时间不随着问题规模n的增加而增长,即使算法中有上千条语句,其执行时间也不过是一个较大的常数。此类算法的时间复杂度是O(1)。 2.1. 交换i和j的内容 因为Θ(2n2+n+1)=n2(即:去低阶项,去掉常数项,去掉高阶项的常参得到),所以T(n)= =O(n2); 2.2. 语句1的频度是n-1,语句2的频度是(n-1)*(2n+1)=2n2-n-1,f(n)=2n2-n-1+(n-1)=2n2-2;又(2n2-2)=n2,该程序的时间复杂度T(n)=O(n2)。 一般情况下,对步进循环语句只需考虑循环体中语句的执行次数,忽略该语句中步长加1、终值判别、控制转移等成分,当有若干个循环语句时,算法的时间复杂度是由嵌套层数最多的循环语句中最内层语句的频度f(n)决定的。 T(n)=2+n+3(n-1)=4n-1=O(n). 取最大值f(n)=log2n,T(n)=O(log2n ) 当i=m, j=k的时候,内层循环的次数为k当i=m时, j 可以取 0,1,...,m-1 , 所以这里最内循环共进行了0+1+...+m-1=(m-1)m/2次所以,i从0取到n, 则循环共进行了: 0+(1-1)*1/2+...+(n-1)n/2=n(n+1)(n-1)/6所以时间复杂度为O(n3). 算法复杂度 标签:问题 依次 应该 mamicode 常见 循环结构 渐进 一点 情况下 原文地址:https://www.cnblogs.com/stu-jyj3621/p/12943531.html
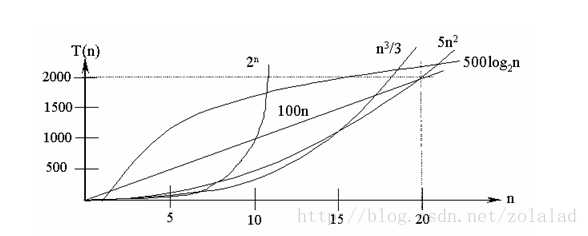
求解算法的时间复杂度
for (i = 1; i )
x++;
for (i = 1; i )
for (j = 1; j )
x++;
几个简单的程序分析法则
几个常见的时间复杂度示例说明:
(1)、O(1)
Temp = i;
i = j;
j = Temp;
(2)、O(n2)
sum = 0; //(一次)
for (i = 1; i //(n + 1次)
for (j = 1; j //(n2次)
sum++; //(n2次)
for (i = 1; i )
{
y = y + 1; //1
for (j = 0; j 2 * n); j++)
x++; //2
}
(3)、O(n)
a = 0;
b = 1; //1
for (i = 1; i //2
{
s = a + b; //3
b = a; //4
a = s; //5
}
(4)、O(log2n)
i = 1; //1
while (i n)
i = i * 2; //2
(5)、O(n3)
for (i = 0; i )
{
for (j = 0; j )
{
for (k = 0; k )
x = x + 2;
}
}
上一篇:算法导论矩阵链