数值分析实验之非线性方程求根（Python 现）

2021-01-16 10:15

阅读：756

标签：NPU def split 牛顿迭代技术 range point lang psi

详细实验指导见上一篇，此处只写内容啦

实验内容：

1. 用二分法求方程x³-3x-1=0在的所有根.要求每个根的误差小于0.001.

提示与要求: (1) 利用精度找到迭代次数;

(2) 由f(x)=3(x²-1)可取隔根区间[-2,-1].[-1,1].[1,2]);

(3) 用程序求各隔根区间内的根.

2. 用不动点迭代求: (1)x³+2x²+10x-20=0的所有根.

或: (2)9x²-sinx-1=0在[0,1]上的一个根.

3. 用Newton迭代法求解下列之一,准确到10^-5:

(1) x³-x-1=0的所有根;

(2) e^x+2^-x+2cosx-6=0位于[0,2]上的根.

实验代码：

• 牛顿迭代法

 1 import math
 2 x=0.5
 3 n = 1
 4 while n ==1 or abs(x-x1)>1e-5:
 5     x1 = x
 6     def F(x1):
 7         return 2**-x+2*math.cos(x)+math.exp(x)-6
 8     def F1(x1):
 9         return math.exp(x)-math.log(2)*(2**-x)-2*math.sin(x)
10     x = x1 - F(x1)/F1(x1)
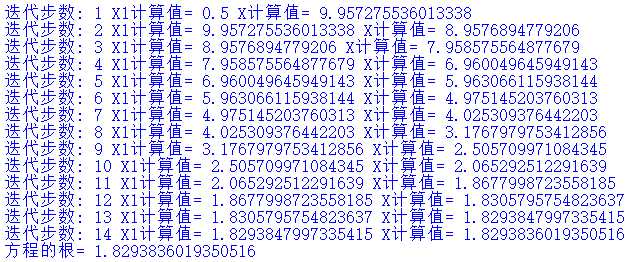
11     print (‘迭代步数:‘,n,‘X1计算值=‘,x1,‘X计算值=‘,x)
12     n = n+1
13 else:
14     print(‘方程的根=‘,(x))

运行结果：

技术图片

• 不动点法

 1 import numpy as np
 2 
 3 def f(x):
 4     return 9*x**2 - np.sin(x) - 1
 5 
 6 def g1(x):
 7     return ((np.sin(x)+1)/9)**0.5
 8 
 9 def g2(x):
10     result = (abs(2 * x + 1))**(1 / 5)
11     if (2 * x - 1)  0:
12         return -result
13     return result
14 
15 def getEpsilon(x, epsilon):
16     maxY = minY = x[0]
17     for each in x:
18         maxY = max(f(each), maxY)
19         minY = min((f(each), minY))
20     epsilon = (maxY - minY) * epsilon
21     return epsilon
22 
23 def getInitialVal(x, N, step, epsilon):
24     initalVal = []
25     for i in range(N + 1):
26         y1, y2, y3 = f(x - step), f(x), f(x + step)
27         if (y1 * y2 and (i != 0):
28             initalVal.append((x + x - step) / 2)
29         if ((y2 - y1) * (y3 - y2) and (abs(y2)  epsilon):
30             initalVal.append(x)
31         x += step
32 
33     return initalVal
34 
35 def findFixedPoint(initalVal, delta,epsilon):
36     points = []
37     for each in initalVal:
38         if (abs(g1(each)) ):
39             points.append(iteration(each, g1, delta,epsilon))
40         else:
41             points.append(iteration(each, g2, delta,epsilon))
42     return points
43 
44 def iteration(p1, g, delta,epsilon):
45     while True:
46         p2 = g(p1)
47         err =abs(p2-p1)
48         relerr = err/(abs(p2)+epsilon)
49         if error relerrdelta:
50             return p2
51         p1 = p2
52                     
53 def main():
54     a, b, c = input().split(‘ ‘)
55     a = float(a)
56     b = float(b)
57     c = int(c)
58     delta = 10 ** (-c)
59     N = 8
60     epsilon = 0.01
61     step = (b - a) / N
62     x = np.arange(a, b + epsilon, epsilon)
63     
64     epsilon2 = getEpsilon(x,epsilon)
65     initalVal = getInitialVal(a, N, step, epsilon2)
66     ans = findFixedPoint(initalVal, delta,epsilon)
67 
68     for each in ans:
69         print(‘方程的根为：%.6f‘ % each)
70         
71 if __name__ == ‘__main__‘:
72     main()