DirectX11 Windows Windows SDK--28 计算着色器:波浪(水波)
2021-01-16 12:14
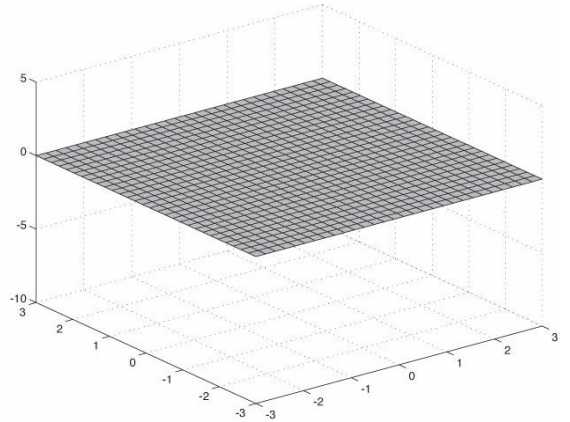
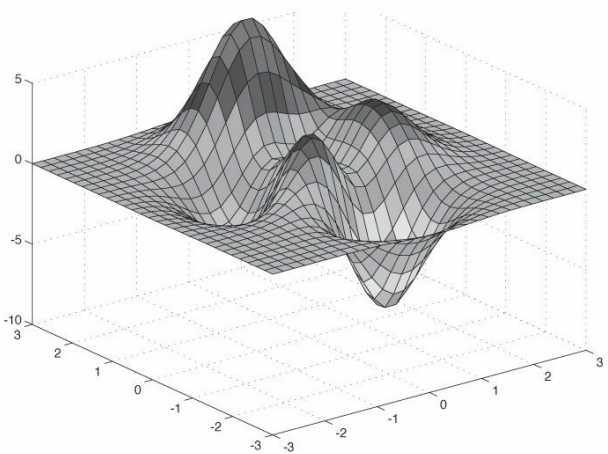
标签:redis osi 水平 二次 完成 缓存 标准化 副本 线性 有关计算着色器的基础其实并不是很多。接下来继续讲解如何使用计算着色器实现水波效果,即龙书中所实现的水波。但是光看代码可是完全看不出来是在做什么的。个人根据书中所给的参考书籍找到了对应的实现原理,但是里面涉及到比较多的物理公式。因此,要看懂这一章需要有高数功底(求导、偏导、微分方程),我会把推导过程给列出来。 本章演示项目还用到了其他的一些效果,在学习本章之前建议先了解如下内容: 学习目标: DirectX11 With Windows SDK完整目录 Github项目源码 欢迎加入QQ群: 727623616 可以一起探讨DX11,以及有什么问题也可以在这里汇报。 我们可以使用一个函数\(y=f(x, z)\)来表示一个曲面,在xz平面内构造一个栅格来近似地表示这个曲面。其中的每个四边形都是由两个三角形所构成的,接下来再利用该函数计算出每个栅格点处的高度即可。 如下图所示,我们先在xz平面内“铺设”一层栅格 然后我们再运用函数\(y=f(x, z)\)来为每个栅格点获取对应的y坐标。再利用\((x, f(x, z), z)\)的所有顶点构造出地形栅格 由以上分析可知,我们首先需要完成的就是来构建xz平面内的栅格。若规定一个m行n列的栅格,那么栅格包含m * n个四边形,即对应2 * m * n个三角形,顶点数为(m + 1) * (n + 1)。 在Geometry中创建地形的方法比较复杂,后三行的形参是根据(x, z)坐标来分别确定出高度y、法向量n和颜色c的函数: 我们的代码是从左下角开始,逐渐向右向上地计算出其余顶点坐标。需要注意的是,纹理坐标是以左上角为坐标原点,U轴朝右,V轴朝下。 下面的代码展示了如何生成栅格顶点: 其中需要额外了解的是切线向量的产生。由于要让切线向量能够与xOy平面平行,需要先让法向量投影到xOy平面,然后再得到对应的未经标准化的切线向量,如下图所示: 正弦函数适合用于表示起伏不定的山坡,一种二维山川地形的函数为: \[
y(x,z)=\frac{3}{10}(zsin(\frac{1}{10}x)+xcos(\frac{1}{10}z))
\] 其在(x, y, z)处未经标准化的法向量为: \[
\mathbf{n}=(-\frac{\partial{y}}{\partial{x}}, 1, -\frac{\partial{y}}{\partial{z}})
\] 其中y对x和对z的偏导分别为: 因此创建上述地形的函数可以写成: 当然,Lambda函数不理解,你也可以写成这样: 在许多游戏中,你可能会看到有水面流动的场景,实际上他们不一定是真正的流体,而有可能只是一个正在运动的水体表面。出于运行效率的考虑,这些效果的实现或多或少涉及到数学公式或者物理公式。 本节我们只讨论龙书所实现的方法,即使用波动方程来表现局部位置激起的水波。它的公式推导比较复杂,但是用心看下去的会应该还是能看得懂的。 话不多说,接下来我们需要啃硬骨头了。 波动方程是一个描述在持续张力作用下的一维绳索或二维表面的某一点处的运动。在一维情况下,我们可以考虑将一个富有弹性的绳索紧紧绑在两端(有轻微拉伸),让绳索落在x轴上来派生出一维的波动方程。我们假定当前的绳索在每一点处的线密度(单位长度下的质量)都是恒等的 令函数\(z(x,t)\)代表绳索在x点处,t时刻的垂直位移量。当绳索在z方向产生位移时,表明绳子正在被拉伸。由牛顿第二定律,我们可以知道在t时刻内,位于\(x=s\)和\(x=s+\Delta x\)之间的绳索段在合力\(\mathbf{F}(x, t)\)的作用下,加速度为: \[
\mathbf{a}(x,t)=\frac{\mathbf{F}(x,t)}{\rho\Delta x} \tag{28.1}
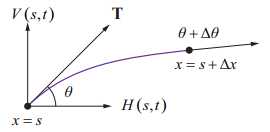
\] 让\(\theta+\Delta\theta\)表示另一个端点\(x=s+\Delta x\)处切线向量与x轴的夹角。这样作用在该端点上的张力的水平分量\(H(s+\Delta x,t)\)和垂直分量\(V(s+\Delta x,t)\)则表示为: 作用在\(x=s\)和\(x=s+\Delta x\)之间的绳索段的垂直合力会在z方向产生一个加速度。由于垂直加速度等于位置函数\(z(x,t)的二阶导\),因此有: 将方程组(28.2)联立,我们可以写成: 由于H(t)并不依赖于x,我们又可以写成: 满足一维波动方程的解有无穷多个,例如一种常见的波函数形式为\(z(x,t)=Asin(\omega(t-\frac{x}{v}))\),函数随着时间的推移图像如下: 然而方程(28.13)仅包含了张力,没有考虑到其他阻力因素,这导致波的平均振幅并不会有任何损耗。我们可以给方程组添加一个与张力方向相反,且与点的运动速度有关的粘性阻尼力: 带粘性阻尼力的二维波动方程(28.14)可以通过可分离变量的形式解出来。然而它的解十分复杂,需要大规模的实时模拟演算。取而代之的是,我们将使用一种数值上的技术来模拟波在流体表面的传播。 假定我们的流体表面可以表示成一个n×m的矩形栅格,如下图所示。 其中d为两个邻近顶点在x方向的距离及y方向的距离(规定相等),t为时间间隔。我们用\(z(i, j, k)\)来表示顶点的位移量,其中i和j分别要满足\(0\leq i 此外,我们需要施加边界条件,让处在边缘的顶点位移量固定为0.内部顶点的偏移则可以使用(28.14)方程,采用近似导数的方法计算出来。如下图所示,我们可以通过在x方向上计算顶点 \[
\begin{equation} \begin{split}
\frac{\partial}{\partial x}z(i,j,k) &= \frac{\frac{z(i,j,k)-z(i-1,j,k)}{d}+\frac{z(i+1,j,k)-z(i,j,k)}{d}}{2} \&=\frac{z(i+1,j,k)-z(i-1,j,k)}{2d} \\end{split} \end{equation} \tag{28.15}
\] 同理,我们取顶点 该公式要求我们使用x轴距离为2的顶点 \[
\frac{{\partial}^2}{{\partial}t^2}z(i,j,k)=\frac{z(i,j,k+1)-2z(i,j,k)+z(i,j,k-1)}{t^2} \tag{28.23}
\] 联立z对t的一阶偏导(公式28.17)以及二阶偏导(公式28.21、28.22、28.23),带粘性阻尼力的二维波动方程可以表示为: 我们想要能够在传递模拟间隔t来确定下一次模拟位移量\(z(i,j,k+1)\),现在我们已经知道当前位移量\(z(i,j,k)\)和上一次模拟的位移量\(z(i,j,k-1)\)。因此\(z(i,j,k+1)\)的解为: 如果波速 假定我们拥有一个n×m顶点数组(其任意\(z(i,j,0)=0\)和\(z(i,j,1)=0\)),现在让某处顶点被抬高使得\(z(i_0, j_0, 0)=h\)和\(z(i_0, j_0, 1)=h\),h是一个非0位移值。若该处顶点被释放了2t时间,此时式子(28.25)中第三个加法部分的值为0,故有: 又或者,给定距离d和波速c,我们能够计算出最大的时间间隔t。对不等式(28.29)乘上\((-\mu t + 2)\)来简化得到: 现在我们需要准备两个二维顶点位置数组,其中一个数组表示的是当前模拟所有顶点的位置,而另一个数组则表示的是上一次模拟所有顶点的位置。当我们计算新的位移时,将下一次模拟的结果直接写在存放上一次模拟顶点的数组即可(可以观察公式28.25,我们需要的是当前顶点上一次模拟、当前模拟的数据,以及当前模拟相邻四个顶点的数据,因此其他顶点在计算位移量的时候不会有影响)。 为了执行光照计算,我们还需要为每个顶点获取正确的法向量以及可能正确的切线向量。对于顶点坐标(i, j),未标准化的,与x轴对齐的切向量T和与y轴对齐的切线向量B如下: 要意识到两次模拟期间的时间间隔必须是恒定的,而不是依据帧间隔。不同游戏运行帧数不同,因此在帧速率较高的情况下,必须采用一定的机制保证在经过足够多的时间后才更新位置。 利用上述方式实现的波浪有两种代码实现形式: 其中前者的效率一般不如后者(在Debug模式下差别过于明显,而在Release模式下好很多),但实现起来比较简单。 这里两种方法都已经实现了,按顺序讲解。 基类WavesRender定义及Init过程如下: Init方法将公式(28.25)的三个重要参数先初始化,以供后续计算使用。 CPUWavesRender的定义如下: 其中顶点的位置我们只保留了两个副本,即当前模拟和上一次模拟的。而由于在计算出下一次模拟的结果后,我们就可以抛弃掉上一次模拟的结果。因此我们可以直接把结果写在存放上一次模拟的位置,然后再进行交换即可。此时原本是当前模拟的数据则变成了上一次模拟的数据,而下一次模拟的结果则变成了当前模拟的数据。顶点的法向量只需要在完成了下一次模拟后再更新,因此也不需要多余的副本了。 在使用 由于我们施加了边界0的条件,因此不能对边界区域激起波浪。在修改高度时,我们还对目标点的相邻四个顶点也修改了高度使得一开始的波浪不会看起来太突兀: 之前提到,两次模拟期间的时间间隔必须是恒定的,而不是依据帧间隔。因此在设置好初始的时间步长后,每当经历了大于时间步长的累积时间就可以进行更新了。同样在更新过程中我们要始终限制边界值为0。虽然公式复杂,但好在实现过程并不复杂。详细见代码: 这里的绘制跟之前用的 相比CPU计算法,GPU计算法的实现则更为复杂了。因为它不仅需要用到计算着色器,还需要跑到绘制基本物体的特效那边做一些修改才能用。 首先计算着色器部分完成的是激起波浪和更新波浪的部分,分为两个函数: 由于全部过程交给了GPU完成,现在我们需要有三个UAV,两个用于输入,一个用于输出。并且由于我们指定了线程组内部包含16x16个线程,在C++初始化 此外,因为GPU对边界外的良好定义,这使得我们不需要约束调用Disturb的索引条件。 紧接着就是要修改 然后是修改 可以看到,顶点y坐标的值和法向量的计算都移步到了顶点着色器上。 因为我们对位移贴图的采样是要取出与当前顶点相邻的4个顶点对应的4个像素,故不能使用含有线性插值法的采样器来采样。因此我们还需要在 其中 计算工作都交给GPU了,这里CPU也就负责提供所需的内容,然后再调度计算着色器即可。最后一定要把绑定到CS的UAV撤下来,避免资源同时作为一个地方的输入和另一个地方的输出。 需要注意的是,这三个位移贴图是循环使用的。调度完成之后,原本是上一次模拟的纹理将用于等待下一次模拟的输出,而当前模拟的纹理则变成上一次模拟的纹理,下一次模拟的纹理则变成了当前模拟的纹理。这种循环交换方式称之为Ping-Pong交换: 跟CPU的绘制区别基本上就在注释部分了: 从这一章开始带着我的光追显卡来跑渲染效果了(相比以前的集成显卡),帧数会有明显的提升 下图演示了GPU绘制的水波效果。由于限制了10M上传,只能勉强看到这一小段了。 测试帧数如下: Debug的话又是vector那边惹出的问题,忽略不计。 只不过当前的样例跟龙书的样例都没有处理好视角带来的过度混合问题,个人暂时也没有解决的办法: 本文的算法实现参考的是 Mathematics for 3D Game Programming and Computer Graphics, Third Edition,书内页码443开始。群内可以下载。 DirectX11 With Windows SDK完整目录 Github项目源码 欢迎加入QQ群: 727623616 可以一起探讨DX11,以及有什么问题也可以在这里汇报。 DirectX11 Windows Windows SDK--28 计算着色器:波浪(水波) 标签:redis osi 水平 二次 完成 缓存 标准化 副本 线性 原文地址:https://www.cnblogs.com/X-Jun/p/12225736.html前言
章节内容
11 混合状态
17 利用几何着色器实现公告板效果(雾效部分)
26 计算着色器:入门
27 计算着色器:双调排序(非双调排序部分)
用三角形栅格表示地形
生成栅格顶点
template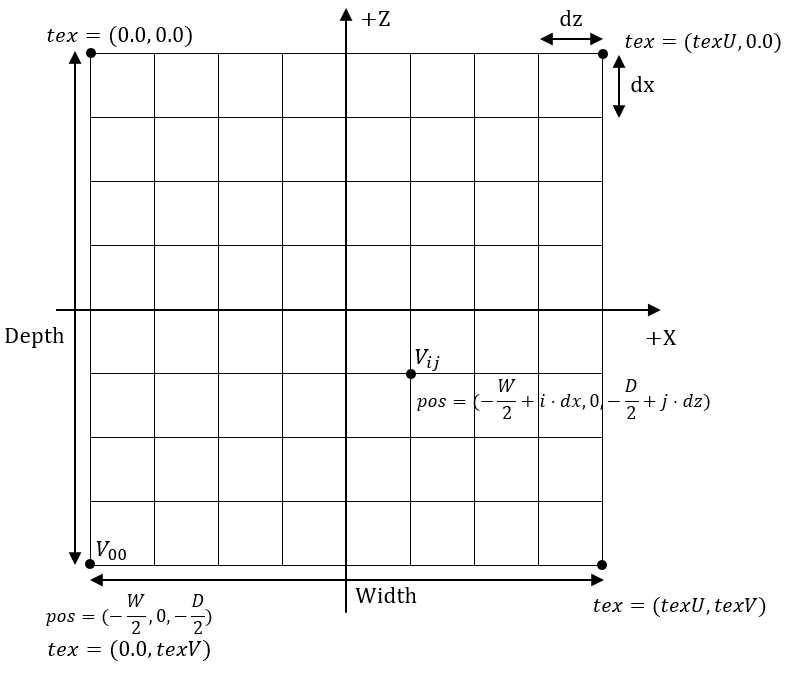
template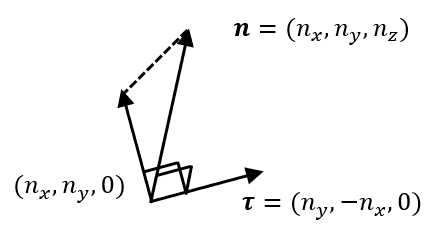
一种表示山峰的函数
\[
\frac{\partial{y}}{\partial{x}}=\frac{3}{10}(\frac{1}{10}zcos(\frac{1}{10}x)+cos(\frac{1}{10}z))\\frac{\partial{y}}{\partial{z}}=\frac{3}{10}(sin(\frac{1}{10}x)-\frac{1}{10}xsin(\frac{1}{10}z))
\]
MeshDatafloat GetHillsHeight(float x, float z)
{
return 0.3f * (z * sinf(0.1f * x) + x * cosf(0.1f * z));
}
XMFLOAT3 GetHillsNormal(float x, float z)
{
return XMFLOAT3(-0.03f * z * cosf(0.1f * x) - 0.3f * cosf(0.1f * z), 1.0f,
-0.3f * sinf(0.1f * x) + 0.03f * x * sinf(0.1f * z));
}
MeshData流体模拟
波动方程的推导
ρ,并且沿着绳索在该点处受到沿着切线的方向持续的张力T。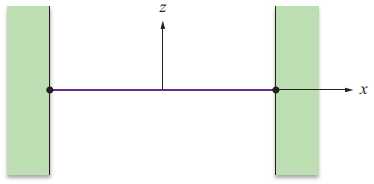
在下面的公式中,我们可以将位于\(x=s\)和\(x=s+\Delta x\)之间的绳索段的两个端点所受的力分解成水平方向和竖直方向的力,得到\(H(x,t)\)和\(V(x,t)\)。让θ表示绳索在\(x=s\)处切向量与x轴方向的夹角。由于张力T沿着切线方向作用,水平分量\(H(s,t)\)和垂直分量\(V(s,t)\)可以表示为:
\[
H(s,t)=Tcos\theta \V(s,t)=Tsin\theta \tag{28.2}
\]
\[
H(s+\Delta x,t)=Tcos(\theta + \Delta\theta) \V(s+\Delta x,t)=Tsin(\theta + \Delta\theta) \tag{28.3}
\]
对于小幅度的运动,我们假定绳索段的水平合力为0,这样绳索段的加速度仅仅包含垂直方向。因此,对于\(x=s\)与\(x=s+\Delta x\)之间的绳索段,我们有下面的公式:
\[
H(s+\Delta x, t) - H(s, t) = 0 \tag{28.4}
\]
这样H函数就不需要依赖x了,我们可以用\(H(t)\)取代\(H(x,t)\)。
\[
a_z(s,t)=\frac{{\partial}^2}{{\partial}t^2}z(s,t)=\frac{V(s+\Delta x,t)-V(s,t)}{\rho\Delta x} \tag{28.5}
\]
等式两边乘上ρ,然后让\(\Delta x\)趋向于0,此时等式右边正好为偏导数的定义:
\[
\rho\frac{{\partial}^2}{{\partial}t^2}z(s,t)=\lim_{\Delta x \to 0}\frac{V(s+\Delta x,t)-V(s,t)}{\Delta x} \tag{28.6}
\]
因此又有:
\[
\rho\frac{{\partial}^2}{{\partial}t^2}z(s,t)=\frac{\partial}{{\partial}x}V(s,t) \tag{28.7}
\]
\[
V(s, t)=H(t)tan\theta \tag{28.8}
\]
因为θ是绳索在X轴方向与切线之间的夹角,\(\tan\theta\)正好也是函数z(x, t)在s处的斜率,因此:
\[
V(s, t)=H(t)\frac{\partial}{\partial x}z(s,t) \tag{28.9}
\]
即:
\[
\rho\frac{{\partial}^2}{{\partial}t^2}z(s,t)=\frac{\partial}{\partial x}[H(t)\frac{\partial}{\partial x}z(s,t)] \tag{28.10}
\]
\[
\rho\frac{{\partial}^2}{{\partial}t^2}z(s,t)=H(t)\frac{{\partial}^2}{\partial x^2}z(s,t) \tag{28.11}
\]
对于小幅度的运动,\(cos\theta\)接近于1(此时水平分量的力为0),因此我们用\(H(t)\)来近似表示张力T。让\(c^2=T/\rho\),我们现在得到了一维的波动方程:
\[
\frac{{\partial}^2 z}{{\partial}t^2}=c^2\frac{{\partial}^2 z}{\partial x^2} \tag{28.12}
\]
同理,二维的波动方程可以通过添加一个y项得到:
\[
\frac{{\partial}^2 z}{{\partial}t^2}=c^2(\frac{{\partial}^2 z}{\partial x^2}+\frac{{\partial}^2 z}{\partial y^2}) \tag{28.13}
\]
常数c具有单位时间距离的尺度,因此可以表示速度。事实上我们也不会证明c实际上就是波沿着绳索或表面传递的速度。这是有意义的,因为波的速度随介质所受张力T的变大而增加,随介质密度μ的减小而减小。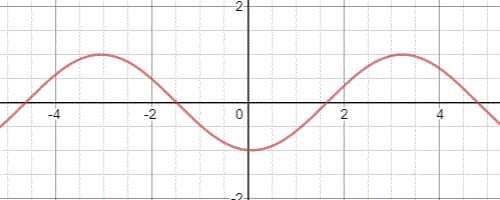
\[
\frac{{\partial}^2 z}{{\partial}t^2}=c^2(\frac{{\partial}^2 z}{\partial x^2}+\frac{{\partial}^2 z}{\partial y^2})-\mu\frac{\partial z}{\partial t} \tag{28.14}
\]
其中非负实数μ代表了液体的粘性,用来控制水面的波什么时候能够平静下来。μ越大,水波消亡的速度越快。对于水来说,通常它的μ值会比较小,使得水波能够存留比较长的时间;但对于油来说,它的μ值会比较大一些,因此水波消亡的速度会比较快。近似导数
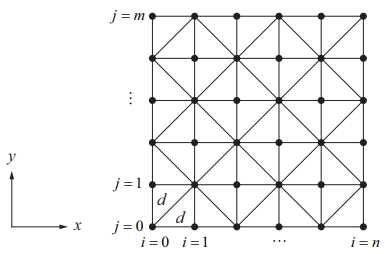
[i][j]分别和它的相邻的两个顶点[i-1][j]和[i+1][j]的微分的平均值\(\frac{\Delta z}{\Delta x}\)来逼近具有坐标[i][j]的顶点上与x轴对齐的切线。这样就有\(\Delta x = d\),我们将偏导数\(\frac{\partial z}{\partial x}\)定义为: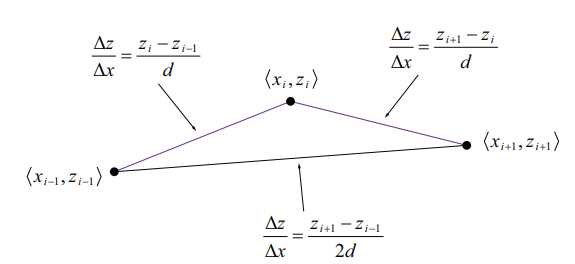
[i][j]的两个y方向上的相邻顶点[i][j-1]和[i][j+1]来近似计算z对于y的偏导数:
\[
\frac{\partial}{\partial y}z(i,j,k) =\frac{z(i,j+1,k)-z(i,j-1,k)}{2d} \tag{28.16}
\]
至于时间,我们可以通过计算顶点在当前时刻分别与上一个时刻和下一个时刻的平均位移差来定义z对时间t偏导\(\frac{\Delta z}{\Delta t}\):
\[
\frac{\partial}{\partial t}z(i,j,k) =\frac{z(i,j,k+1)-z(i,j,k-1)}{2t} \tag{28.17}
\]
二阶偏导也可以使用和一阶偏导相同的方法来计算。假如我们已经计算出了顶点[i-1][j]和[i+1][j]的偏移z对x的一阶偏导数,那么我们就可以得到两者平均差值:
\[
\begin{equation} \begin{split}
\Delta[\frac{\partial}{\partial x}z(i,j,k)] &= \frac{\frac{\partial}{\partial x}z(i+1,j,k)-\frac{\partial}{\partial x}z(i,j,k)}{2} + \frac{\frac{\partial}{\partial x}z(i,j,k)-\frac{\partial}{\partial x}z(i-1,j,k)}{2} \&=\frac{\frac{\partial}{\partial x}z(i+1,j,k)-\frac{\partial}{\partial x}z(i-1,j,k)}{2} \\end{split} \end{equation} \tag{28.18}
\]
将方程(28.15)带入上式,可以得到:
\[
\begin{equation} \begin{split}
\Delta[\frac{\partial}{\partial x}z(i,j,k)] &= \frac{\frac{z(i+2,j,k)-z(i,j,k)}{2d} - \frac{z(i,j,k)-z(i-2,j,k)}{2d}}{2} \&=\frac{z(i+2,j,k)-2z(i,j,k)+z(i-2,j,k)}{4d} \\end{split} \end{equation} \tag{28.19}
\]
除以d使得我们可以得到\(\Delta(\frac{\partial z}{\partial x})/\Delta x\),对应二阶偏导:
\[
\frac{{\partial}^2}{{\partial}x^2}z(i,j,k)=\frac{z(i+2,j,k)-2z(i,j,k)+z(i-2,j,k)}{4d^2} \tag{28.20}
\][i+2][j]和[i-2][j]来计算二阶偏导。不过相邻的两个顶点就没有用到了,我们可以基于顶点[i][j]将x轴缩小一半,使用距离最近的两个相邻点[i+1][j]和[i-1][j]来计算二阶偏导:
\[
\frac{{\partial}^2}{{\partial}x^2}z(i,j,k)=\frac{z(i+1,j,k)-2z(i,j,k)+z(i-1,j,k)}{d^2} \tag{28.21}
\]
同理可得:
\[
\frac{{\partial}^2}{{\partial}y^2}z(i,j,k)=\frac{z(i,j+1,k)-2z(i,j,k)+z(i,j-1,k)}{d^2} \tag{28.22}
\]求出水面位移
\[
\frac{z(i,j,k+1)-2z(i,j,k)+z(i,j,k-1)}{t^2}=c^{2}\frac{z(i+1,j,k)-2z(i,j,k)+z(i-1,j,k)}{d^2}\+c^{2}\frac{z(i,j+1,k)-2z(i,j,k)+z(i,j-1,k)}{d^2}-\mu\frac{z(i,j,k+1)-z(i,j,k-1)}{2t} \tag{28.24}
\]
\[
z(i,j,k+1)=\frac{4-8c^2t^2/d^2}{\mu t+2}z(i,j,k)+\frac{\mu t-2}{\mu t+2}z(i,j,k-1)\+\frac{2c^2t^2/d^2}{\mu t+2}[z(i+1,j,k)+z(i-1,j,k)+z(i,j+1,k)+z(i,j-1,k)] \tag{28.25}
\]
这条公式正是我们想要的。其中常量部分可以预先计算出来,只剩下3个带t的因式和4个加法需要给网格中每个顶点进行运算。c过快,或者时间段t太长,上述式子的偏移量有可能趋向于无穷。为了保持结果是有穷的,我们需要给上式确定额外的条件,并且要保证在我们抬高一个顶点并释放后能够确保水波逐渐远离顶点位置。
\[
\begin{equation} \begin{split}
z(i,j,2)&=\frac{4-8c^2t^2/d^2}{\mu t+2}z(i,j,1)+\frac{\mu t-2}{\mu t+2}z(i,j,0)\&=\frac{2-8c^2t^2/d^2+\mu t}{\mu t+2}h
\end{split} \end{equation} \tag{28.26}
\]
为了让顶点向周围平坦的水面移动,它在2t时刻的位移必须要比在t时刻的更小一些。因此就有:
\[
\left| z(i_0, j_0, 2)\right|
代入方程(28.26),有:
\[
\left| \frac{2-8c^2t^2/d^2 + \mu t}{\mu t + 2} \right|\cdot\left| h\right|
因此,
\[
-1
把速度c解出来,我们可以得到:
\[
0
这告诉我们对于公式(28.25),给定两个顶点的距离d以及时间间隔t,波速c必须小于上式的最大值
\[
0
由于t>0,中间部分恒大于0,去掉左半部分解一元二次不等式,并舍去t\[
0
使用c区间和t区间外的值会导致位移z的结果呈指数级爆炸。代码实现
\[
\mathbf{T}=(1,0,\frac{\partial}{\partial x}z(i,j,k))\\mathbf{B}=(0,1,\frac{\partial}{\partial y}z(i,j,k)) \tag{28.33}
\]
用公式28.15和28.16代入28.33,可得:
\[
\mathbf{T}=(1,0,\frac{z(i+1,j,k)-z(i-1,j,k)}{2d})\\mathbf{B}=(0,1,\frac{z(i,j+1,k)-z(i,j-1,k)}{2d}) \tag{28.34}
\]
经过叉乘后可以得到未经标准化的法向量:
\[
\begin{equation} \begin{split}
\mathbf{N} &= \mathbf{T}\times\mathbf{B} \&=\begin{vmatrix}
\mathbf{i} & \mathbf{j} & \mathbf{k} \1 & 0 & \frac{z(i+1,j,k)-z(i-1,j,k)}{2d} \0 & 1 & \frac{z(i,j+1,k)-z(i,j-1,k)}{2d} \\end{vmatrix} \&= (-\frac{z(i+1,j,k)-z(i-1,j,k)}{2d},-\frac{z(i,j+1,k)-z(i,j-1,k)}{2d}, 1)
\end{split} \end{equation} \tag{28.35}
\]
对上述向量乘上2d的倍数并不会改变它的方向,但可以消除除法:
\[
\mathbf{T}=(2d,0,z(i+1,j,k)-z(i-1,j,k))\\mathbf{B}=(0,2d,z(i,j+1,k)-z(i,j-1,k))\\mathbf{N}=(z(i-1,j,k)-z(i+1,j,k),z(i,j-1,k)-z(i,j+1,k), 2d) \tag{28.36}
\]
注意这里T和B并没有相互正交。CPU计算法
基类WavesRender
class WavesRender
{
public:
templateCPUWavesRender类
class CpuWavesRender : public WavesRender
{
public:
CpuWavesRender() = default;
~CpuWavesRender() = default;
// 不允许拷贝,允许移动
CpuWavesRender(const CpuWavesRender&) = delete;
CpuWavesRender& operator=(const CpuWavesRender&) = delete;
CpuWavesRender(CpuWavesRender&&) = default;
CpuWavesRender& operator=(CpuWavesRender&&) = default;
HRESULT InitResource(ID3D11Device* device,
const std::wstring& texFileName, // 纹理文件名
UINT rows, // 顶点行数
UINT cols, // 顶点列数
float texU, // 纹理坐标U方向最大值
float texV, // 纹理坐标V方向最大值
float timeStep, // 时间步长
float spatialStep, // 空间步长
float waveSpeed, // 波速
float damping, // 粘性阻尼力
float flowSpeedX, // 水流X方向速度
float flowSpeedY); // 水流Y方向速度
void Update(float dt);
// 在顶点[i][j]处激起高度为magnitude的波浪
// 仅允许在1 m_Vertices; // 保存当前模拟结果的顶点二维数组的一维展开
std::vectorCpuWavesRender之前固然是要调用InitResource先进行初始化的,但现在我们跳过这部分代码,直接看和算法相关的几个方法。CpuWavesRender::Disturb方法--激起波浪
void CpuWavesRender::Disturb(UINT i, UINT j, float magnitude)
{
// 不要对边界处激起波浪
assert(i > 1 && i 1 && j CpuWavesRender::Update方法--更新波浪
void CpuWavesRender::Update(float dt)
{
m_AccumulateTime += dt;
m_TexOffset.x += m_FlowSpeedX * dt;
m_TexOffset.y += m_FlowSpeedY * dt;
// 仅仅在累积时间大于时间步长时才更新
if (m_AccumulateTime > m_TimeStep)
{
m_isUpdated = true;
// 仅仅对内部顶点进行更新
for (size_t i = 1; i CpuWavesRender::Draw方法--绘制波浪
BasicEffect是可以直接适配的,动态顶点缓冲区的更新只需要在数据发生变化时再进行,以减少CPU向GPU的数据传输次数:void CpuWavesRender::Draw(ID3D11DeviceContext* deviceContext, BasicEffect& effect)
{
// 更新动态缓冲区的数据
if (m_isUpdated)
{
m_isUpdated = false;
D3D11_MAPPED_SUBRESOURCE mappedData;
deviceContext->Map(m_pVertexBuffer.Get(), 0, D3D11_MAP_WRITE_DISCARD, 0, &mappedData);
memcpy_s(mappedData.pData, m_VertexCount * sizeof(VertexPosNormalTex),
m_Vertices.data(), m_VertexCount * sizeof(VertexPosNormalTex));
deviceContext->Unmap(m_pVertexBuffer.Get(), 0);
}
UINT strides[1] = { sizeof(VertexPosNormalTex) };
UINT offsets[1] = { 0 };
deviceContext->IASetVertexBuffers(0, 1, m_pVertexBuffer.GetAddressOf(), strides, offsets);
deviceContext->IASetIndexBuffer(m_pIndexBuffer.Get(), DXGI_FORMAT_R32_UINT, 0);
effect.SetMaterial(m_Material);
effect.SetTextureDiffuse(m_pTextureDiffuse.Get());
effect.SetWorldMatrix(XMLoadFloat4x4(&m_WorldMatrix));
effect.SetTexTransformMatrix(XMMatrixScaling(m_TexU, m_TexV, 1.0f) * XMMatrixTranslationFromVector(XMLoadFloat2(&m_TexOffset)));
effect.Apply(deviceContext);
deviceContext->DrawIndexed(m_IndexCount, 0, 0);
}GPU计算法
HLSL代码
// Waves.hlsli
// 用于更新模拟
cbuffer cbUpdateSettings : register(b0)
{
float g_WaveConstant0;
float g_WaveConstant1;
float g_WaveConstant2;
float g_DisturbMagnitude;
int2 g_DisturbIndex;
float2 g_Pad;
}
RWTexture2D// WavesDisturb_CS.hlsl
#include "Waves.hlsli"
[numthreads(1, 1, 1)]
void CS( uint3 DTid : SV_DispatchThreadID )
{
// 我们不需要进行边界检验,因为:
// --读取超出边界的区域结果为0,和我们对边界处理的需求一致
// --对超出边界的区域写入并不会执行
uint x = g_DisturbIndex.x;
uint y = g_DisturbIndex.y;
float halfMag = 0.5f * g_DisturbMagnitude;
// RW型资源允许读写,所以+=是允许的
g_Output[uint2(x, y)] += g_DisturbMagnitude;
g_Output[uint2(x + 1, y)] += halfMag;
g_Output[uint2(x - 1, y)] += halfMag;
g_Output[uint2(x, y + 1)] += halfMag;
g_Output[uint2(x, y - 1)] += halfMag;
}// WavesUpdate.hlsl
#include "Waves.hlsli"
[numthreads(16, 16, 1)]
void CS( uint3 DTid : SV_DispatchThreadID )
{
// 我们不需要进行边界检验,因为:
// --读取超出边界的区域结果为0,和我们对边界处理的需求一致
// --对超出边界的区域写入并不会执行
uint x = DTid.x;
uint y = DTid.y;
g_Output[uint2(x, y)] =
g_WaveConstant0 * g_PrevSolInput[uint2(x, y)].x +
g_WaveConstant1 * g_CurrSolInput[uint2(x, y)].x +
g_WaveConstant2 * (
g_CurrSolInput[uint2(x, y + 1)].x +
g_CurrSolInput[uint2(x, y - 1)].x +
g_CurrSolInput[uint2(x + 1, y)].x +
g_CurrSolInput[uint2(x - 1, y)].x);
}GpuWavesRender时,我们也应该指定行顶点数和列顶点数都为16的倍数。BasicEffect里面用到的顶点着色器以支持计算着色器的位移贴图:#include "LightHelper.hlsli"
Texture2D g_DiffuseMap : register(t0); // 物体纹理
Texture2D g_DisplacementMap : register(t1); // 位移贴图
SamplerState g_SamLinearWrap : register(s0); // 线性过滤+Wrap采样器
SamplerState g_SamPointClamp : register(s1); // 点过滤+Clamp采样器
cbuffer CBChangesEveryInstanceDrawing : register(b0)
{
matrix g_World;
matrix g_WorldInvTranspose;
matrix g_TexTransform;
}
cbuffer CBChangesEveryObjectDrawing : register(b1)
{
Material g_Material;
}
cbuffer CBChangesEveryFrame : register(b2)
{
matrix g_View;
float3 g_EyePosW;
float g_Pad;
}
cbuffer CBDrawingStates : register(b3)
{
float4 g_FogColor;
int g_FogEnabled;
float g_FogStart;
float g_FogRange;
int g_TextureUsed;
int g_WavesEnabled; // 开启波浪绘制
float2 g_DisplacementMapTexelSize; // 位移贴图两个相邻像素对应顶点之间的x,y方向间距
float g_GridSpatialStep; // 栅格空间步长
}
cbuffer CBChangesOnResize : register(b4)
{
matrix g_Proj;
}
cbuffer CBChangesRarely : register(b5)
{
DirectionalLight g_DirLight[5];
PointLight g_PointLight[5];
SpotLight g_SpotLight[5];
}
struct VertexPosNormalTex
{
float3 PosL : POSITION;
float3 NormalL : NORMAL;
float2 Tex : TEXCOORD;
};
struct InstancePosNormalTex
{
float3 PosL : POSITION;
float3 NormalL : NORMAL;
float2 Tex : TEXCOORD;
matrix World : World;
matrix WorldInvTranspose : WorldInvTranspose;
};
struct VertexPosHWNormalTex
{
float4 PosH : SV_POSITION;
float3 PosW : POSITION; // 在世界中的位置
float3 NormalW : NORMAL; // 法向量在世界中的方向
float2 Tex : TEXCOORD;
};
BasicObject_VS.hlsl。因为水面是单个物体,不需要改到BasicInstance_VS.hlsl里面:// BasicObject_VS.hlsl
#include "Basic.hlsli"
// 顶点着色器
VertexPosHWNormalTex VS(VertexPosNormalTex vIn)
{
VertexPosHWNormalTex vOut;
// 绘制水波时用到
if (g_WavesEnabled)
{
// 使用映射到[0,1]x[0,1]区间的纹理坐标进行采样
vIn.PosL.y += g_DisplacementMap.SampleLevel(g_SamLinearWrap, vIn.Tex, 0.0f).r;
// 使用有限差分法估算法向量
float du = g_DisplacementMapTexelSize.x;
float dv = g_DisplacementMapTexelSize.y;
float left = g_DisplacementMap.SampleLevel(g_SamPointClamp, vIn.Tex - float2(du, 0.0f), 0.0f).r;
float right = g_DisplacementMap.SampleLevel(g_SamPointClamp, vIn.Tex + float2(du, 0.0f), 0.0f).r;
float top = g_DisplacementMap.SampleLevel(g_SamPointClamp, vIn.Tex - float2(0.0f, dv), 0.0f).r;
float bottom = g_DisplacementMap.SampleLevel(g_SamPointClamp, vIn.Tex + float2(0.0f, dv), 0.0f).r;
vIn.NormalL = normalize(float3(-right + left, 2.0f * g_GridSpatialStep, bottom - top));
}
matrix viewProj = mul(g_View, g_Proj);
vector posW = mul(float4(vIn.PosL, 1.0f), g_World);
vOut.PosW = posW.xyz;
vOut.PosH = mul(posW, viewProj);
vOut.NormalW = mul(vIn.NormalL, (float3x3) g_WorldInvTranspose);
vOut.Tex = mul(float4(vIn.Tex, 0.0f, 1.0f), g_TexTransform).xy;
return vOut;
}RenderStates.h中添加点过滤+Clamp采样:ComPtrGpuWavesRender类
GpuWavesRender类定义如下:class GpuWavesRender : public WavesRender
{
public:
GpuWavesRender() = default;
~GpuWavesRender() = default;
// 不允许拷贝,允许移动
GpuWavesRender(const GpuWavesRender&) = delete;
GpuWavesRender& operator=(const GpuWavesRender&) = delete;
GpuWavesRender(GpuWavesRender&&) = default;
GpuWavesRender& operator=(GpuWavesRender&&) = default;
// 要求顶点行数和列数都能被16整除,以保证不会有多余
// 的顶点被划入到新的线程组当中
HRESULT InitResource(ID3D11Device* device,
const std::wstring& texFileName, // 纹理文件名
UINT rows, // 顶点行数
UINT cols, // 顶点列数
float texU, // 纹理坐标U方向最大值
float texV, // 纹理坐标V方向最大值
float timeStep, // 时间步长
float spatialStep, // 空间步长
float waveSpeed, // 波速
float damping, // 粘性阻尼力
float flowSpeedX, // 水流X方向速度
float flowSpeedY); // 水流Y方向速度
void Update(ID3D11DeviceContext* deviceContext, float dt);
// 在顶点[i][j]处激起高度为magnitude的波浪
// 仅允许在1 m_pNextSolution; // 缓存下一次模拟结果的y值二维数组
ComPtrm_pNextSolution、m_pCurrSolution、m_pPrevSolution都为2D位移贴图,它们不仅可能会作为计算着色器的输入、输出(UAV),还可能会作为提供给顶点着色器的位移y输入用于计算(SRV)。GpuWavesRender::Disturb方法--激起波浪
void GpuWavesRender::Disturb(ID3D11DeviceContext* deviceContext, UINT i, UINT j, float magnitude)
{
// 更新常量缓冲区
D3D11_MAPPED_SUBRESOURCE mappedData;
m_CBUpdateSettings.waveInfo = XMFLOAT4(0.0f, 0.0f, 0.0f, magnitude);
m_CBUpdateSettings.index = XMINT4(j, i, 0, 0);
deviceContext->Map(m_pConstantBuffer.Get(), 0, D3D11_MAP_WRITE_DISCARD, 0, &mappedData);
memcpy_s(mappedData.pData, sizeof m_CBUpdateSettings, &m_CBUpdateSettings, sizeof m_CBUpdateSettings);
deviceContext->Unmap(m_pConstantBuffer.Get(), 0);
// 设置计算所需
deviceContext->CSSetShader(m_pWavesDisturbCS.Get(), nullptr, 0);
ID3D11UnorderedAccessView* m_UAVs[1] = { m_pCurrSolutionUAV.Get() };
deviceContext->CSSetConstantBuffers(0, 1, m_pConstantBuffer.GetAddressOf());
deviceContext->CSSetUnorderedAccessViews(2, 1, m_UAVs, nullptr);
deviceContext->Dispatch(1, 1, 1);
// 清除绑定
m_UAVs[0] = nullptr;
deviceContext->CSSetUnorderedAccessViews(2, 1, m_UAVs, nullptr);
}GpuWavesRender::Update方法--更新波浪
void GpuWavesRender::Update(ID3D11DeviceContext* deviceContext, float dt)
{
m_AccumulateTime += dt;
m_TexOffset.x += m_FlowSpeedX * dt;
m_TexOffset.y += m_FlowSpeedY * dt;
// 仅仅在累积时间大于时间步长时才更新
if (m_AccumulateTime > m_TimeStep)
{
// 更新常量缓冲区
D3D11_MAPPED_SUBRESOURCE mappedData;
m_CBUpdateSettings.waveInfo = XMFLOAT4(m_K1, m_K2, m_K3, 0.0f);
deviceContext->Map(m_pConstantBuffer.Get(), 0, D3D11_MAP_WRITE_DISCARD, 0, &mappedData);
memcpy_s(mappedData.pData, sizeof m_CBUpdateSettings, &m_CBUpdateSettings, sizeof m_CBUpdateSettings);
deviceContext->Unmap(m_pConstantBuffer.Get(), 0);
// 设置计算所需
deviceContext->CSSetShader(m_pWavesUpdateCS.Get(), nullptr, 0);
deviceContext->CSSetConstantBuffers(0, 1, m_pConstantBuffer.GetAddressOf());
ID3D11UnorderedAccessView* pUAVs[3] = { m_pPrevSolutionUAV.Get(), m_pCurrSolutionUAV.Get(), m_pNextSolutionUAV.Get() };
deviceContext->CSSetUnorderedAccessViews(0, 3, pUAVs, nullptr);
// 开始调度
deviceContext->Dispatch(m_NumCols / 16, m_NumRows / 16, 1);
// 清除绑定
pUAVs[0] = pUAVs[1] = pUAVs[2] = nullptr;
deviceContext->CSSetUnorderedAccessViews(0, 3, pUAVs, nullptr);
//
// 对缓冲区进行Ping-pong交换以准备下一次更新
// 上一次模拟的缓冲区不再需要,用作下一次模拟的输出缓冲
// 当前模拟的缓冲区变成上一次模拟的缓冲区
// 下一次模拟的缓冲区变换当前模拟的缓冲区
//
auto resTemp = m_pPrevSolution;
m_pPrevSolution = m_pCurrSolution;
m_pCurrSolution = m_pNextSolution;
m_pNextSolution = resTemp;
auto srvTemp = m_pPrevSolutionSRV;
m_pPrevSolutionSRV = m_pCurrSolutionSRV;
m_pCurrSolutionSRV = m_pNextSolutionSRV;
m_pNextSolutionSRV = srvTemp;
auto uavTemp = m_pPrevSolutionUAV;
m_pPrevSolutionUAV = m_pCurrSolutionUAV;
m_pCurrSolutionUAV = m_pNextSolutionUAV;
m_pNextSolutionUAV = uavTemp;
m_AccumulateTime = 0.0f; // 重置时间
}
}GpuWavesRender::Draw方法--绘制波浪
void GpuWavesRender::Draw(ID3D11DeviceContext* deviceContext, BasicEffect& effect)
{
UINT strides[1] = { sizeof(VertexPosNormalTex) };
UINT offsets[1] = { 0 };
deviceContext->IASetVertexBuffers(0, 1, m_pVertexBuffer.GetAddressOf(), strides, offsets);
deviceContext->IASetIndexBuffer(m_pIndexBuffer.Get(), DXGI_FORMAT_R32_UINT, 0);
effect.SetWavesStates(true, 1.0f / m_NumCols, 1.0f / m_NumCols, m_SpatialStep); // 开启波浪绘制
effect.SetMaterial(m_Material);
effect.SetTextureDiffuse(m_pTextureDiffuse.Get());
effect.SetTextureDisplacement(m_pCurrSolutionSRV.Get()); // 需要额外设置位移贴图
effect.SetWorldMatrix(XMLoadFloat4x4(&m_WorldMatrix));
effect.SetTexTransformMatrix(XMMatrixScaling(m_TexU, m_TexV, 1.0f) * XMMatrixTranslationFromVector(XMLoadFloat2(&m_TexOffset)));
effect.Apply(deviceContext);
deviceContext->DrawIndexed(m_IndexCount, 0, 0);
effect.SetTextureDisplacement(nullptr); // 解除占用
effect.SetWavesStates(false); // 关闭波浪绘制
effect.Apply(deviceContext);
}演示
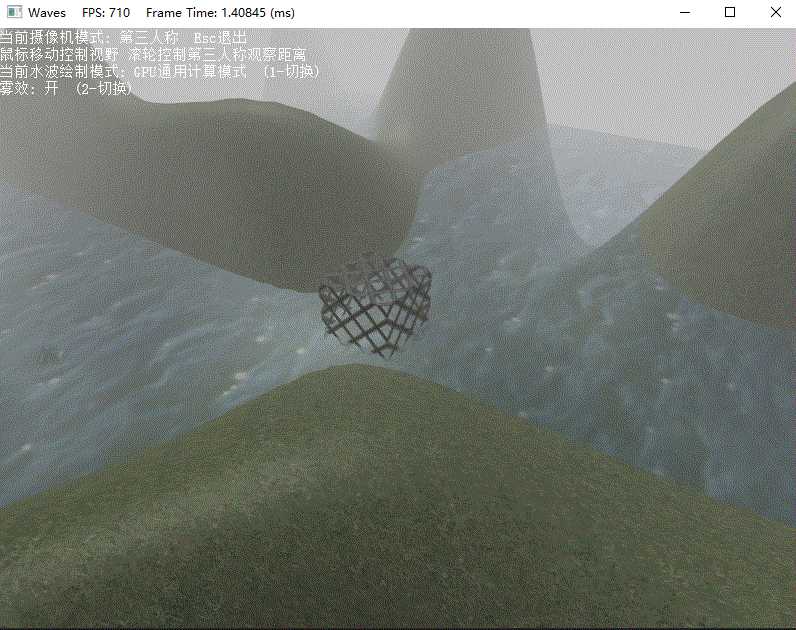
GPU通用计算模式
CPU动态更新模式
Debug x64模式
3500
27
Release x64模式
4200
3900
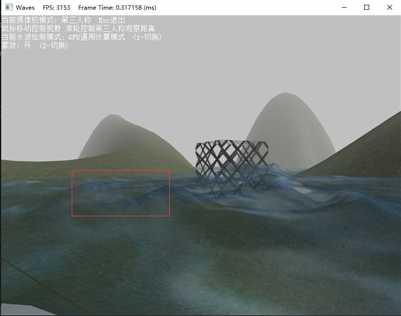
练习题
参考资料
文章标题:DirectX11 Windows Windows SDK--28 计算着色器:波浪(水波)
文章链接:http://soscw.com/index.php/essay/42708.html