LSTM的备胎,用卷积处理时间序列——TCN与因果卷积(理论+Python实践)
2021-01-16 13:13
标签:图像 不用 mod 链接 nsa -o utils 问题 ado TCN全称Temporal Convolutional Network,时序卷积网络,是在2018年提出的一个卷积模型,但是可以用来处理时间序列。 时间序列预测,最容易想到的就是那个马尔可夫模型: 就是计算某一个时刻的输出值,已知条件就是这个时刻之前的所有特征值。上面公式中,P表示概率,可以不用管这个,\(y_k\)表示k时刻的输出值(标签),\(x_k\)表示k时刻的特征值。 如果使用LSTM或者是GRU这样的RNN模型,自然是可以处理这样的时间序列模型的,毕竟RNN生来就是为了这个的。 但是这个时间序列模型,宏观上思考的话,其实就是对这个这个时刻之前的数据做某个操作,然后生成一个标签,回想一下在卷积在图像中的操作,其实有异曲同工。(这里不理解也无妨,因为我之前搞了一段时间图像处理,所以对卷积相对熟悉一点)。 假设有一个时间序列,总共有五个时间点,比方说股市,有一个股票的价格波动:[10,13,12,14,15]: 卷积核是2,那么可想而知,对上面5个数据做一个卷积核为2的卷积是什么样子的: 可以看到是输入是5个数据,但是经过卷积,变成4个数据了,在图像中有一个概念是通过padding来保证卷积前后特征图尺寸不变,所以在时间序列中,依然使用padding来保证尺寸不变: 总之,现在我们大概能理解,对时间序列卷积的大致流程了,也就是对一维数据卷积的过程(图像卷积算是二维)。 下面看如何使用Pytorch来实现一维卷积: 其中的参数跟二维卷积非常类似,也是有通道的概念的。这个好好品一下,一维数据的通道跟图像的通道一样,是根据不同的卷积核从相同的输入中抽取出来不同的特征。kernel_size=2之前也说过了,padding=1也没问题,不过这个公式中假如输入5个数据+padding=1,会得到6个数据,最后一个数据被舍弃掉。dilation是膨胀系数,下面的下面会讲。 之前已经讲了一维卷积的过程了,那么因果卷积,其实就是一维卷积的一种应用吧算是。 假设想用上面讲到的概念,做一个股票的预测决策模型,然后希望决策模型可以考虑到这个时间点之前的4个时间点的股票价格进行决策,总共有3种决策: 所以其实就是一个分类问题。因为要求视野域是4,所以按照上面的设想,要堆积3个卷积核为2的1维卷积层: 股票数据,往往是按照分钟记录的,那少说也是十万、百万的数据量,我们决策,想要考虑之前1000个时间点呢?视野域要是1000,那意味着要999层卷积?啥计算机吃得消这样的计算。所以引入了膨胀因果卷积。 然后我们依然实现上面那个例子,每次决策想要视野域为4: 那么假设事业域要是8呢?那就再加一个dilation=4的卷积。dilation的值是2的次方,然后视野域也是2的次方的增长,那么就算是要1000视野域,那十层大概就行了。 这里有一个动图,挺好看的: TCN基本就是一个膨胀因果卷积的过程,只是上面我们实现因果卷积就只有一个卷积层。而TCN的稍微复杂一点(但是不难!) 如果不了解的话,emm,我要安利我的博文了2333: 可以看出来,这个函数就是第一个数据到倒数第chomp_size的数据,这个chomp_size就是padding的值。比方说输入数据是5,padding是1,那么会产生6个数据没错吧,那么就是保留前5个数字。 最后就是TCN的主网络了: 咋用的呢?就是num_inputs就是输入数据的通道数,一般就是1; num_channels应该是个列表,其他的np.array也行,比方说是[2,1]。那么整个TCN模型包含两个TemporalBlock,整个模型共有4个卷积层,第一个TemporalBlock的两个卷积层的膨胀系数\(dilation=2^0=1\),第二个TemporalBlock的两个卷积层的膨胀系数是\(dilation=2^1=2\). 没了,整个TCN挺简单的,如果之前学过PyTorch和图像处理的一些内容,然后用TCN来上手时间序列,效果会和LGM差不多。(根据最近做的一个比赛),没有跟Wavenet比较过,Wavenet的pytorch资源看起来怪复杂的,因为wavenet是用来处理音频生成的,会更加复杂一点。 总之TCN就这么多,谢谢大家。 LSTM的备胎,用卷积处理时间序列——TCN与因果卷积(理论+Python实践) 标签:图像 不用 mod 链接 nsa -o utils 问题 ado 原文地址:https://www.cnblogs.com/PythonLearner/p/12925732.html什么是TCN
卷积如何处理时间序列
一维卷积

TCN中,或者说因果卷积中,使用的卷积核大小都是2,我也不知道为啥不用更大的卷积核,看论文中好像没有说明这个,如果有小伙伴知道原因或者有猜想,可以下方评论处一起讨论讨论。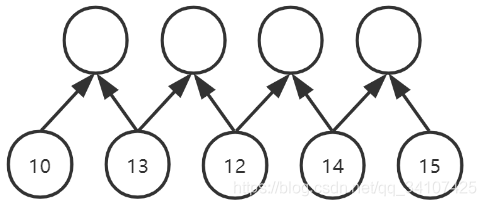
五个数据经过一次卷积,可以变成四个数据,但是每一个卷积后的数据都是基于两个原始数据得到的,所以说,目前卷积的视野域是2。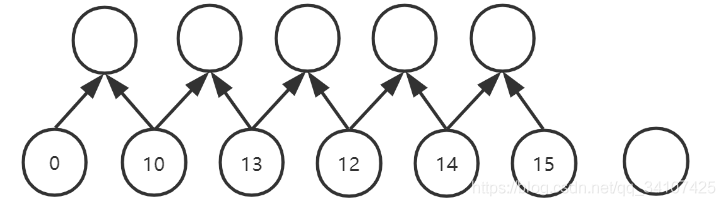
padding是左右两头都增加0,如果padding是1的话,就是上图的效果,其实会产生6个新数据,但是秉着:“输入输出尺寸相同”和“我们不能知道未来的数据”,所以最后边那个未来的padding,就省略掉了,之后再代码中会体现出来。net = nn.Conv1d(in_channels=1,out_channels=1,kernel_size=2,stride=1,padding=1,dilation=1)
因果卷积
TCN的论文链接:
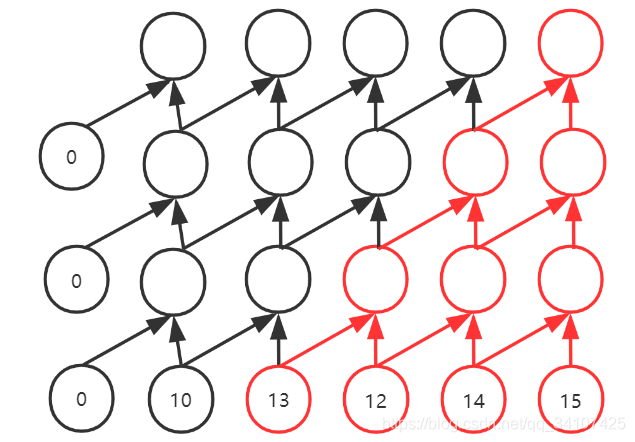
三次卷积,可以让最后的输出,拥有4个视野域。就像是上图中红色的部分,就是做出一个决策的过程。膨胀因果卷积
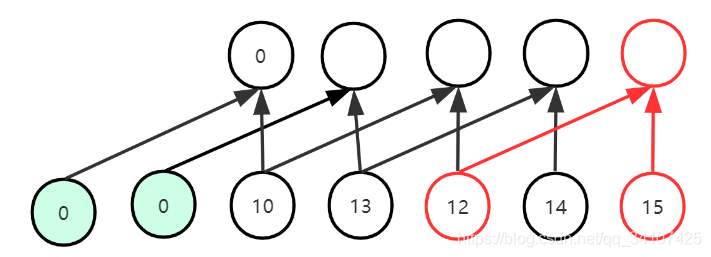
如图,这个就是dilation=2的时候的情况,与之前的区别有两个: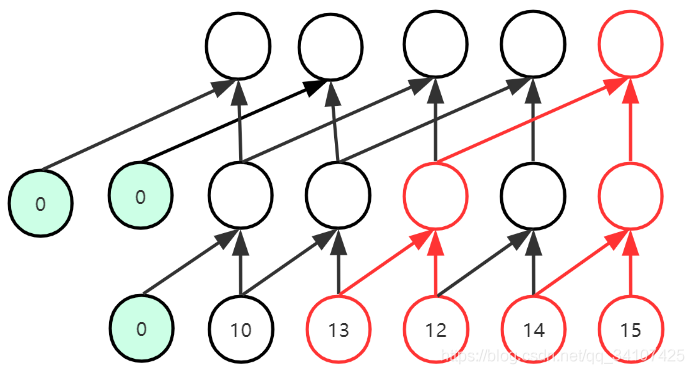
可以看到,第一次卷积使用dilation=1的卷积,然后第二次使用dilation=2的卷积,这样通过两次卷积就可以实现视野域是4.
TCN结构
关于Resnet的内容:【从零学习PyTorch】 如何残差网络resnet作为pre-model +代码讲解+残差网络resnet是个啥其实不看也行,不妨碍理解TCN模型的PyTorch实现(最好了解一点PyTorch)
从零学习pytorch 第5课 PyTorch模型搭建三要素# 导入库
import torch
import torch.nn as nn
from torch.nn.utils import weight_norm
# 这个函数是用来修剪卷积之后的数据的尺寸,让其与输入数据尺寸相同。
class Chomp1d(nn.Module):
def __init__(self, chomp_size):
super(Chomp1d, self).__init__()
self.chomp_size = chomp_size
def forward(self, x):
return x[:, :, :-self.chomp_size].contiguous()
# 这个就是TCN的基本模块,包含8个部分,两个(卷积+修剪+relu+dropout)
# 里面提到的downsample就是下采样,其实就是实现残差链接的部分。不理解的可以无视这个
class TemporalBlock(nn.Module):
def __init__(self, n_inputs, n_outputs, kernel_size, stride, dilation, padding, dropout=0.2):
super(TemporalBlock, self).__init__()
self.conv1 = weight_norm(nn.Conv1d(n_inputs, n_outputs, kernel_size,
stride=stride, padding=padding, dilation=dilation))
self.chomp1 = Chomp1d(padding)
self.relu1 = nn.ReLU()
self.dropout1 = nn.Dropout(dropout)
self.conv2 = weight_norm(nn.Conv1d(n_outputs, n_outputs, kernel_size,
stride=stride, padding=padding, dilation=dilation))
self.chomp2 = Chomp1d(padding)
self.relu2 = nn.ReLU()
self.dropout2 = nn.Dropout(dropout)
self.net = nn.Sequential(self.conv1, self.chomp1, self.relu1, self.dropout1,
self.conv2, self.chomp2, self.relu2, self.dropout2)
self.downsample = nn.Conv1d(n_inputs, n_outputs, 1) if n_inputs != n_outputs else None
self.relu = nn.ReLU()
self.init_weights()
def init_weights(self):
self.conv1.weight.data.normal_(0, 0.01)
self.conv2.weight.data.normal_(0, 0.01)
if self.downsample is not None:
self.downsample.weight.data.normal_(0, 0.01)
def forward(self, x):
out = self.net(x)
res = x if self.downsample is None else self.downsample(x)
return self.relu(out + res)
class TemporalConvNet(nn.Module):
def __init__(self, num_inputs, num_channels, kernel_size=2, dropout=0.2):
super(TemporalConvNet, self).__init__()
layers = []
num_levels = len(num_channels)
for i in range(num_levels):
dilation_size = 2 ** i
in_channels = num_inputs if i == 0 else num_channels[i-1]
out_channels = num_channels[i]
layers += [TemporalBlock(in_channels, out_channels, kernel_size, stride=1, dilation=dilation_size,
padding=(kernel_size-1) * dilation_size, dropout=dropout)]
self.network = nn.Sequential(*layers)
def forward(self, x):
return self.network(x)
上一篇:关于python中的死锁
下一篇:Python类型注解
文章标题:LSTM的备胎,用卷积处理时间序列——TCN与因果卷积(理论+Python实践)
文章链接:http://soscw.com/index.php/essay/42722.html