排序方法
2021-01-17 13:15
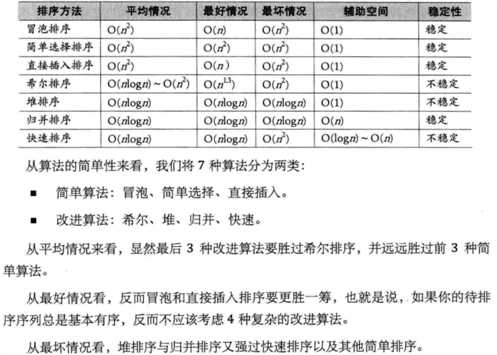
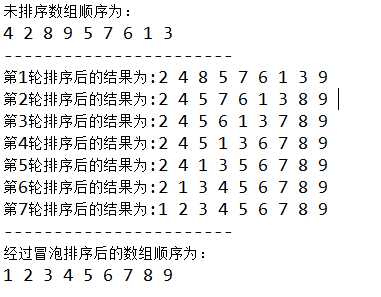
标签:oid 最大的 显示 有序 次数 idt 方法 false OLE 比较: 这个名词的由来很好理解,一般河水中的冒泡,水底刚冒出来的时候是比较小的,随着慢慢向水面浮起会逐渐增大,这物理规律我不作过多解释,大家只需要了解即可。 冒泡算法的运作规律如下: ①、比较相邻的元素。如果第一个比第二个大,就交换他们两个。 ②、对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数(也就是第一波冒泡完成)。 ③、针对所有的元素重复以上的步骤,除了最后一个。 ④、持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。 代码如下: 结果如下: 本来应该是 8 轮排序的,这里我们只进行了 7 轮排序,因为第 7 轮排序之后已经是有序数组了。 冒泡排序解释: 冒泡排序是由两个for循环构成,第一个for循环的变量 i 表示总共需要多少轮比较,第二个for循环的变量 j 表示每轮参与比较的元素下标【0,1,......,length-i】,因为每轮比较都会出现一个最大值放在最右边,所以每轮比较后的元素个数都会少一个,这也是为什么 j 的范围是逐渐减小的。相信大家理解之后快速写出一个冒泡排序并不难。 冒泡排序性能分析: 假设参与比较的数组元素个数为 N,则第一轮排序有 N-1 次比较,第二轮有 N-2 次,如此类推,这种序列的求和公式为: (N-1)+(N-2)+...+1 = N*(N-1)/2 当 N 的值很大时,算法比较次数约为 N2/2次比较,忽略减1。 假设数据是随机的,那么每次比较可能要交换位置,可能不会交换,假设概率为50%,那么交换次数为 N2/4。不过如果是最坏的情况,初始数据是逆序的,那么每次比较都要交换位置。 交换和比较次数都和N2 成正比。由于常数不算大 O 表示法中,忽略 2 和 4,那么冒泡排序运行都需要 O(N2) 时间级别。 其实无论何时,只要看见一个循环嵌套在另一个循环中,我们都可以怀疑这个算法的运行时间为 O(N2)级,外层循环执行 N 次,内层循环对每一次外层循环都执行N次(或者几分之N次)。这就意味着大约需要执行N2次某个基本操作。 选择排序是每一次从待排序的数据元素中选出最小的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完。 分为三步: ①、从待排序序列中,找到关键字最小的元素 ②、如果最小元素不是待排序序列的第一个元素,将其和第一个元素互换 ③、从余下的 N - 1 个元素中,找出关键字最小的元素,重复(1)、(2)步,直到排序结束 代码如下: 运行结果: 选择排序性能分析: 选择排序和冒泡排序执行了相同次数的比较:N*(N-1)/2,但是至多只进行了N次交换。 当 N 值很大时,比较次数是主要的,所以和冒泡排序一样,用大O表示是O(N2) 时间级别。但是由于选择排序交换的次数少,所以选择排序无疑是比冒泡排序快的。当 N 值较小时,如果交换时间比选择时间大的多,那么选择排序是相当快的。 直接插入排序基本思想是每一步将一个待排序的记录,插入到前面已经排好序的有序序列中去,直到插完所有元素为止。 插入排序还分为直接插入排序、二分插入排序、链表插入排序、希尔排序等等,这里我们只是以直接插入排序讲解,后面讲高级排序的时候会将其他的。 代码如下: 运行结果: 插入排序性能分析: 在第一轮排序中,它最多比较一次,第二轮最多比较两次,一次类推,第N轮,最多比较N-1次。因此有 1+2+3+...+N-1 = N*(N-1)/2。 假设在每一轮排序发现插入点时,平均只有全体数据项的一半真的进行了比较,我们除以2得到:N*(N-1)/4。用大O表示法大致需要需要 O(N2) 时间级别。 复制的次数大致等于比较的次数,但是一次复制与一次交换的时间耗时不同,所以相对于随机数据,插入排序比冒泡快一倍,比选择排序略快。 这里需要注意的是,如果要进行逆序排列,那么每次比较和移动都会进行,这时候并不会比冒泡排序快。 上面讲的三种排序,冒泡、选择、插入用大 O 表示法都需要 O(N2) 时间级别。一般不会选择冒泡排序,虽然冒泡排序书写是最简单的,但是平均性能是没有选择排序和插入排序好的。 选择排序把交换次数降低到最低,但是比较次数还是挺大的。当数据量小,并且交换数据相对于比较数据更加耗时的情况下,可以应用选择排序。 在大多数情况下,假设数据量比较小或基本有序时,插入排序是三种算法中最好的选择。 后面我们会讲解高级排序,大O表示法的时间级别将比O(N2)小。 排序方法 标签:oid 最大的 显示 有序 次数 idt 方法 false OLE 原文地址:https://www.cnblogs.com/aaaazzzz/p/12918209.html
1.排序方法与比较

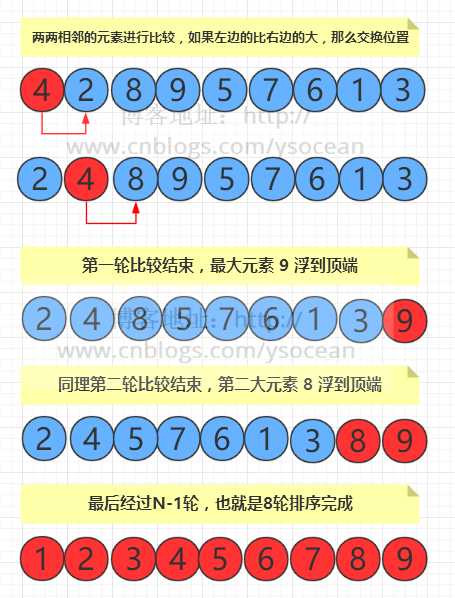
2、冒泡排序

package com.ys.sort;
public class BubbleSort {
public static int[] sort(int[] array){
//这里for循环表示总共需要比较多少轮
for(int i = 1 ; i array[j+1]){
int temp = array[j];
array[j] = array[j+1];
array[j+1] = temp;
flag = false;
}
}
if(flag){
break;
}
//第 i轮排序的结果为
System.out.print("第"+i+"轮排序后的结果为:");
display(array);
}
return array;
}
//遍历显示数组
public static void display(int[] array){
for(int i = 0 ; i
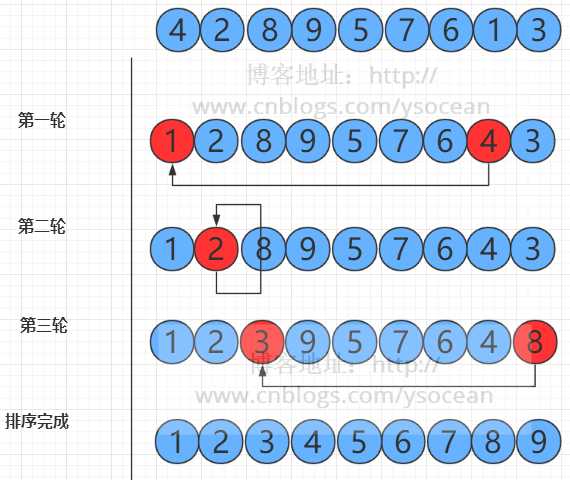
3、选择排序

package com.ys.sort;
public class ChoiceSort {
public static int[] sort(int[] array){
//总共要经过N-1轮比较
for(int i = 0 ; i

4、插入排序

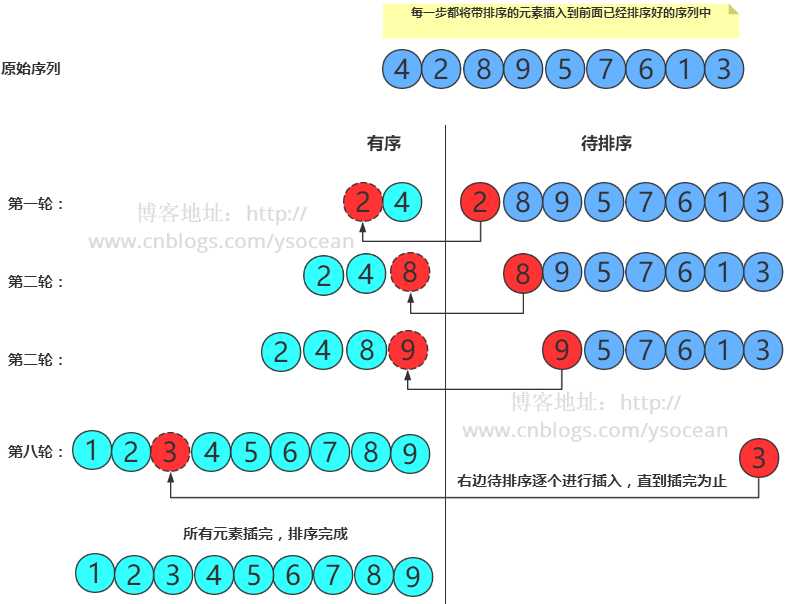
package com.ys.sort;
public class InsertSort {
public static int[] sort(int[] array){
int j;
//从下标为1的元素开始选择合适的位置插入,因为下标为0的只有一个元素,默认是有序的
for(int i = 1 ; i 0 && tmp

5、总结