ResNet
2021-01-18 11:14
标签:lan book ide 卷积神经网络 理解 理想 激活 测试数据 出现 1、ResNet是一种残差网络,咱们可以把它理解为一个子网络,这个子网络经过堆叠可以构成一个很深的网络。 2、但是根据实验表明,随着网络的加深,优化效果反而越差,测试数据和训练数据的准确率反而降低了。这是由于网络的加深会造成梯度爆炸和梯度消失的问题。 目前针对这种现象已经有了解决的方法:对输入数据和中间层的数据进行归一化操作,这种方法可以保证网络在反向传播中采用随机梯度下降(SGD),从而让网络达到收敛。但是,这个方法仅对几十层的网络有用,当网络再往深处走的时候,这种方法就无用武之地了。 为了让更深的网络也能训练出好的效果,何凯明大神提出了一个新的网络结构——ResNet。这个网络结构的想法主要源于VLAD(残差的想法来源)和Highway Network(跳跃连接的想法来源)。 3、ResNet是通过将一层的输入和另一层的输出结果一起作为一个块的输出,假设x是一个块的输入,一块由两层组成,那么他先经过一个卷积层并且relu激活得到F(x),然后F(x)再经过卷积层之后的结果加上之前的输入x得到一个结果,将结果通过relu激活作为该块的输出。对于普通的卷积网络,我们输出的是F(x),但是在ResNet中,我们输出的是H(x) = F(x) + x,但是我们仍然拟合F(x) = H(x) - x.这样有什么好处呢?这样做改变了学习的目标,把原来学习让目标函数等于一个已知的恒定值改变为使输出与输入的残差为0,也就是恒等映射,导致的是,引入残差后映射对输出的变化更为敏感。 4、 残差的思想都是去掉相同的主体部分,从而突出微小的变化。 5、ResNet block有两种,一种两层结构,一种三层结构 6、 咱们要求解的映射为:H(x) 残差:观测值与估计值之间的差。 那么咱们要求解的问题变成了H(x) = F(x)+x。 咱们干嘛非要经过F(x)之后在求解H(x)啊? 现在大家已经理解了为啥只要用F(x)+x来表示H(x)了吧! 注意:如果残差映射(F(x))的结果的维度与跳跃连接(x)的维度不同,那咱们是没有办法对它们两个进行相加操作的,必须对x进行升维操作,让他俩的维度相同时才能计算。 全0填充; Sam Gross and Michael Wilber提出的 ResNet 标签:lan book ide 卷积神经网络 理解 理想 激活 测试数据 出现 原文地址:https://www.cnblogs.com/h694879357/p/13347514.html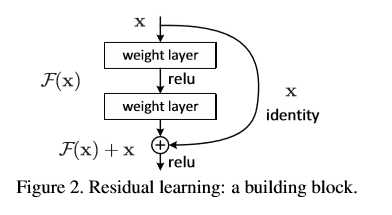
现在咱们将这个问题转换为求解网络的残差映射函数,也就是F(x),其中F(x) = H(x)-x。
这里H(x)就是观测值,x就是估计值(也就是上一层ResNet输出的特征映射)。
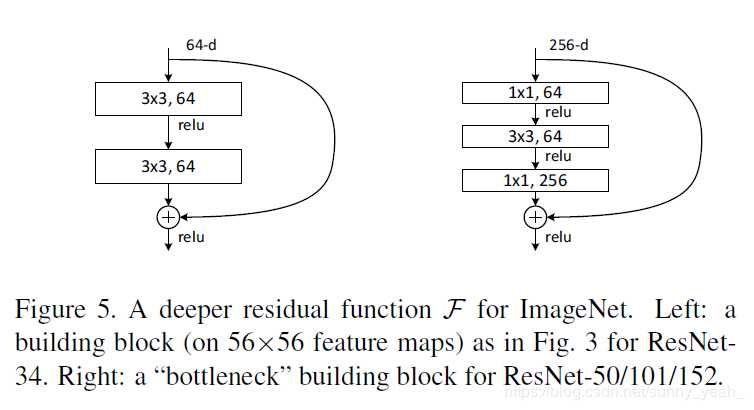
我们一般称x为identity Function,它是一个跳跃连接;称F(x)为ResNet Function。
咱们开始看图说话:如果是采用一般的卷积神经网络的化,原先咱们要求解的是H(x) = F(x)这个值对不?那么,我们现在假设,在我的网络达到某一个深度的时候,咱们的网络已经达到最优状态了,也就是说,此时的错误率是最低的时候,再往下加深网络的化就会出现退化问题(错误率上升的问题)。咱们现在要更新下一层网络的权值就会变得很麻烦,权值得是一个让下一层网络同样也是最优状态才行。对吧?
但是采用残差网络就能很好的解决这个问题。还是假设当前网络的深度能够使得错误率最低,如果继续增加咱们的ResNet,为了保证下一层的网络状态仍然是最优状态,咱们只需要把令F(x)=0就好啦!因为x是当前输出的最优解,为了让它成为下一层的最优解也就是希望咱们的输出H(x)=x的话,是不是只要让F(x)=0就行了?
当然上面提到的只是理想情况,咱们在真实测试的时候x肯定是很难达到最优的,但是总会有那么一个时刻它能够无限接近最优解。采用ResNet的话,也只用小小的更新F(x)部分的权重值就行啦!不用像一般的卷积层一样大动干戈!
它的公式也相当简单(这里给出两层结构的):a[l+2]=Relu(W[l+2](Relu(W[l+1]a[l]+b[l+1])+b[l+2]+a[l])
(不理解这个公式的小伙伴可以跳到我之前关于BP的博客瞅瞅:https://blog.csdn.net/sunny_yeah_/article/details/88560830
升维的方法有两种:
采用1*1卷积。
最后的实验结果表明,ResNet在上百层都有很好的表现,但是当达到上千层了之后仍然会出现退化现象。不过在2016年的Paper中对ResNet的网络结构进行了调整,使得当网络达到上千层的时候仍然具有很好的表现。