算法图解学习系列--第4章--快速排序

标签：运行时   divide   简单的   c语言   基线   nta   ret   连接   部分   

分而治之

D&C（divide and conquer ）是一种著名的递归式问题解决方法。

D&C的工作原理

• 找出简单的基线条件；

• 确定如何缩小问题的规模，使其符合基线条件。

计算数字数组的和

实现方法1

pirint(sum([1, 2, 3]))
# 或者
def sumd(array):
    if len(array) = 0:
        return None
    
    total = 0
    for i in array:
        total += i
    return total
pirint(sumd([1, 2, 3]))

实现方法2

示意图

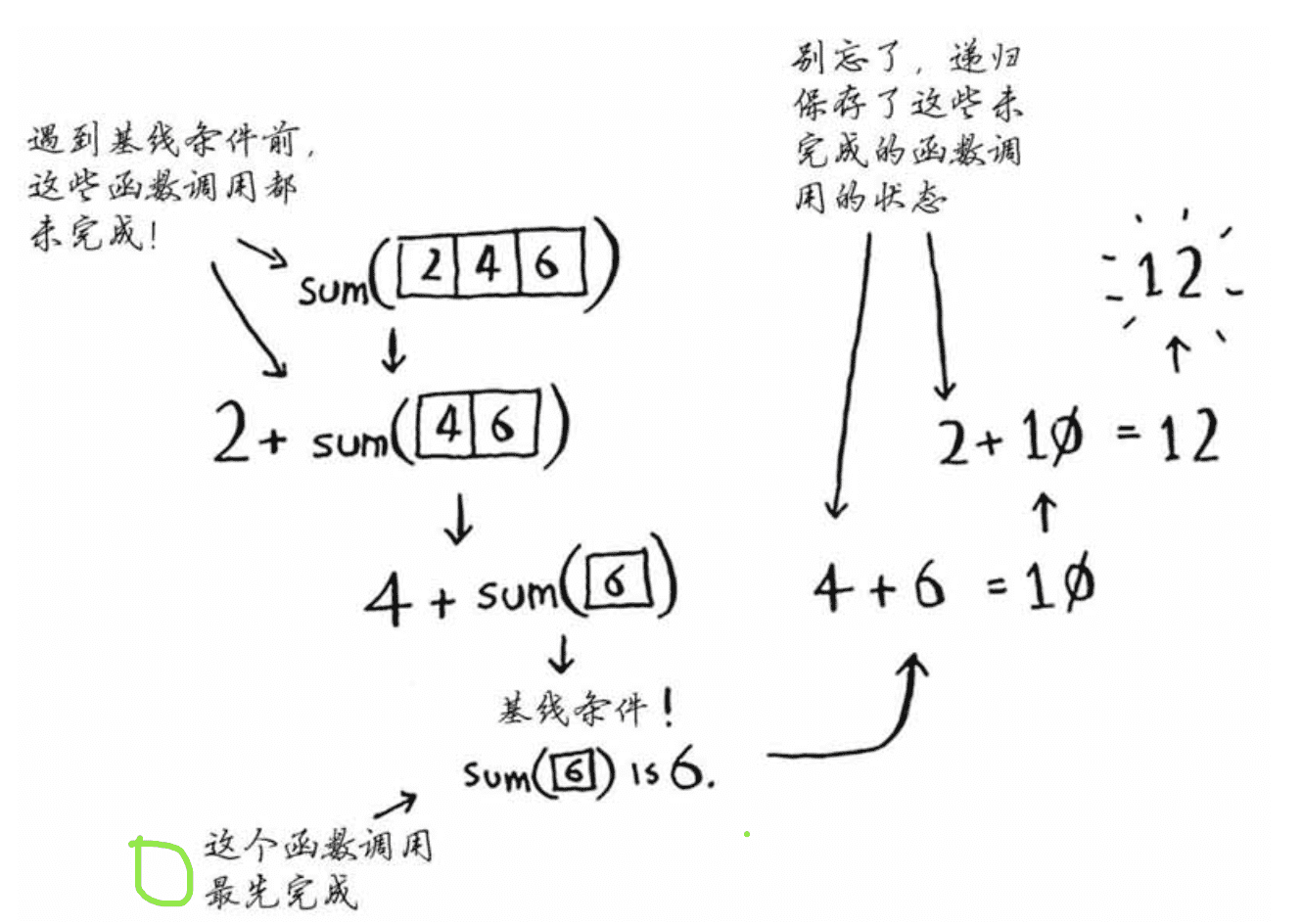
def sumd(array):
    # 首次输入为空列表，直接返回None
    # 有长度的数组是依次减少的，因此不会减少到空列表
    if len(array) == 0:
        return None
    elif len(array) == 1:
        return array[0]
    else:
        return array[0] + sumd(array[1:])
print(sumd([1, 2, 3]))

print(sumd([]))

快速排序

快速排序是一种常用的排序算法，比选择排序快得多。例如，C语言标准库中的函数qsort实现的就是快速排序。快速排序也使用了D&C。

但是，这种排序用了递归，故元素个数受限于栈深。

处理过程简单理解

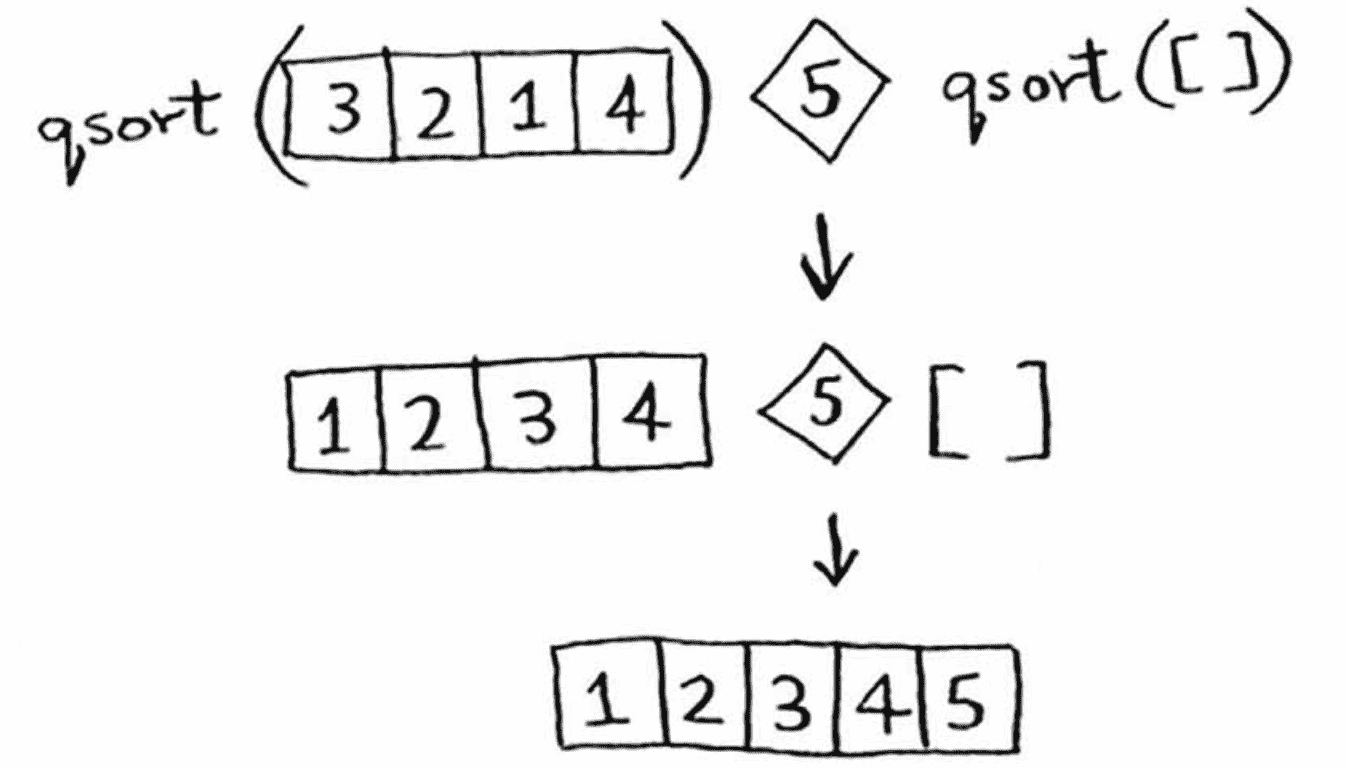
1. 对于数组[5, 2, 1, 4, 3]排序，选取第一个值作为基准值，将小于等于基准值的部分放在一个列表less中，大于等于基准值放在列表greater中

2. less 中的元素小于等于基准值，故只要less中的元素排序后，可以和基准值连接上；对于less这个小数组再利用第1步进行排序

3. 同样的，greater的排序和第2步的less相同。

这里找准基准条件是比较重要的一点

python实现快速排序

def quick_sort(array):
    if len(array)  pivot]
        return quick_sort(less) + [pivot] + quick_sort(greater)

print(quick_sort([10, 2, 7, 4, 1, 2]))

时间复杂度

最佳情况

在这个示例中，层数为O(log n)（用技术术语说，调用栈的高度为O(log n)），而每层需要的时间为O(n)。因此整个算法需要的时间为O(n) ＊ O(log n)=O(n log n)。

在最糟情况下，有O(n)层，因此该算法的运行时间为O(n) ＊ O(n)=O(n2)。

书上说这里的最佳情况也是平均情况，这里还是不太理解。

算法图解学习系列--第4章--快速排序

标签：运行时   divide   简单的   c语言   基线   nta   ret   连接   部分   

原文地址：https://www.cnblogs.com/hiyang/p/12885836.html