算法设计与分析: 2-2 众数问题

 1 package cn.htu.test;
 2 
 3 import java.util.Arrays;
 4 
 5 public class TestZhongShu01 {
 6 
 7     public static void main(String[] args) {
 8         int[] numbers = {1, 2, 2, 2, 3, 5};
 9         
10         int maxNum = Arrays.stream(numbers).max().getAsInt();
11         //.stream()可以把Arrays对象转换为流，然后用stream的.max()找出流的最大元素.作为整数返回getAsInt()
12         //查帮助文档的时候要注意Array和Arrays不同
13         
14         int[] count = new int[maxNum+1];//创建一个count数组，下标从0到maxNum
15         //如此一来，所有范围的数都可以在count数组中以下标的形式找到
16 
17         for(int i=0; i){
18             count[numbers[i]]++;
19             //将numbers数组的情况映射到count数组上去
20         }
21 
22         int tmpCount = 0;
23         int tmpValue = 0;
24         
25 
26         for(int i=0; i){
27             if(count[i] > tmpCount){
28                 tmpCount = count[i];
29                 tmpValue = i;//始终记得count的下标和numbers的元素值对应
30             }
31         }
32 
33         System.out.println("The number: "+tmpValue+" appeared most times: "+tmpCount);
34     }
35 }

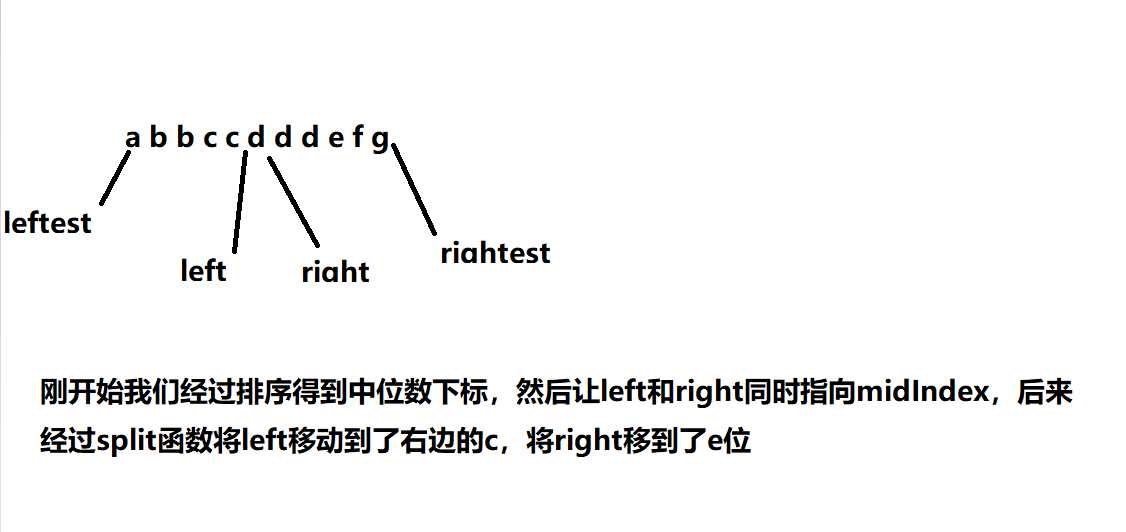
 1 package cn.htu.test;
 2 
 3 import java.util.Arrays;
 4 
 5 public class TestZhongShu01 {
 6     private static int[] numbers = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 1, 1, 2, 2, 3, 4, 5};
 7 
 8     private static int leftest = 0;//数组最左边的下标
 9     private static int rightest = numbers.length-1;//数组的最右边的下标
10     private static int left, right;
11 
12     private static int count=0;
13     private static int number;
14 
15     public static void main(String[] args) {
16 
17         Arrays.sort(numbers);//先进行一次排序
18 
19         mode(leftest, rightest);//将leftrest和rightest，数组两端下标传入自定义函数mode
20 
21         System.out.println("The number: "+number+" appeared most times: "+count);
22     }
23 
24     private static void mode(int l, int r){
25 
26         int midIndex = getMidIndex(l, r);//自定义函数getMidIndex返回中位数下标
27         split(numbers, midIndex, l, r);//传入数组，中间下标，最左下标和最右端下标，最后函数的作用是将left和right下标移动位置，到达中位数的左边
28 
29         if(count ){
30             count = right-left+1;//代表最大重数，刚开始代表中位数的重数
31             number = numbers[midIndex];//代表最大重数对应的众数，刚开始填充的是中位数
32         }
33         //下面是分治法的内核
34         //如果左边的数目或者右边的数目多于最大重数就进行递归
35         if(left-l > count)
36             mode(l, left-1);
37         if(r-right > count)
38             mode(right+1, r);
39     }
40 
41     private static int getMidIndex(int l, int r){
42         return (l+r)/2;
43     }
44 
45     private static void split(int[] numbers, int midIndex, int l, int r)
46     {
47         //用left和right都指向中位数下标
48         left = midIndex;
49         right = midIndex;
50 
51         while (left-1 >=l && numbers[--left] == numbers[midIndex]);//left下标一直左移除非左移的那个数不是和中位数相等
52         while (right+1//right下标一直右移，除非右移的那个数和中位数不相等
53         
54         //循环之后的left和right下标之间的距离就是中位数的重数
55         
56         if(numbers[l] != numbers[midIndex])//把left下标移到中位数左边的那一位，如果相同那就没必要挪动了
57             left++;
58         if(numbers[r] != numbers[midIndex])
59             right--;
60     }
61 }