算法框架之二叉树扩展&二叉搜索树
2021-02-01 10:13
标签:分析 UNC 一个 style int tar png blog 好的 二叉树基础遍历 在上一章以解释过 算法框架之数组&链表&二叉树 【如何判断两棵二叉树是否完全相同?】 先来道开胃菜 应该很好理解 一共会出现三种情况【空的情况(都空+一个空)+非空情况+递归】 1.在谈论写法前 先必须知道其定义吧 二叉搜索树(Binary Search Tree,简称 BST)是一种很常用的的二叉树。它的定义是:一个二叉树中,任意节点的值要大于等于左子树所有节点的值,且要小于等于右边子树的所有节点的值。 【下图就是一个二叉搜索树】 可能想通过上面的【二叉树框架】+【二叉搜索树定义】依葫芦画瓢 搞一个出来 代码如下 看似十分正确!满足【每一个子树】 左 (右侧的子树应该也都大于结点 但6与根10不满足) 是否是框架不适用了?亦或者是开头就想错了? 并不!!只需稍作修改即可 先分析为什么不满足情况? 因为 只考虑了子树结点情况 ,并没考虑之前的根节点情况 因此只需 将其记录 每一项的【最大值/最小值】即可 先来看看普通的树如何找值呢? 那在对二叉搜索树找值时 是否有好的方法呢? 或者说利用【二叉树的特性】 由上述2,3点+【二叉搜索树定义】可得框架 说到底 就是【二叉搜索树之查】的修改版 => 先查到位置 再新建结点 加入即可 注:一般增加操作要求返回根结点 删除是最麻烦的一个操作 要分三种情况【无孩子】【有一个孩子】【有左右孩子】 1、无孩子 十分方便 只需将其删除即可 2、有一个孩子 将其替代之前的位置 3、有两个孩子 此种情况最为麻烦: 1.删除本值,寻找左子树的最大值/右子树的最小值,替换位置 由于只需替换一种 此处用替换左子树最大值为例: 4、 整体【二叉搜索树之删】框架 算法框架之二叉树扩展&二叉搜索树 标签:分析 UNC 一个 style int tar png blog 好的 原文地址:https://www.cnblogs.com/cc123nice/p/12813777.html二叉树扩展
/**
* Definition for ListNode.
* function ListNode (val) {
* this.val = val;
* this.next= null;
* }
*/
/**
* @param {ListNode } root1
* @param {ListNode } root2
*/
*/
function issame(root1,root2){
//如果两结点都为空 必然相同
if(root1 == nul l&& root2 == null)
return true
//【经过上一个条件 没有return的话 说明至少一个不为空,因此还得排除 一个空一个不空的情况】
//如果一个空一个不空 则必不同
if(root1 != null || root2 != null)
return false
// 【上两个条件排除掉空的情况 因此接下来必然有值】
//遇到值不同时 也是表明是不同的树
if(root1.val != root2.val)
return false
return issame(root1.left,root2.left)&&issame(root1.right,root2.right)
}
二叉搜索树
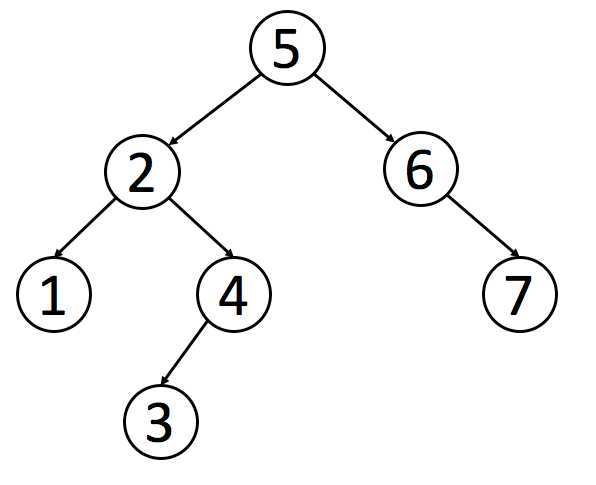
2.在书写判定二叉搜索树时,很容易进入一个误区
function isValidBST(root) {
if (root == null) return true;
if (root.left != null && root.val return false;
if (root.right != null && root.val >= root.right.val) return false;
return isValidBST(root.left)&& isValidBST(root.right);
}
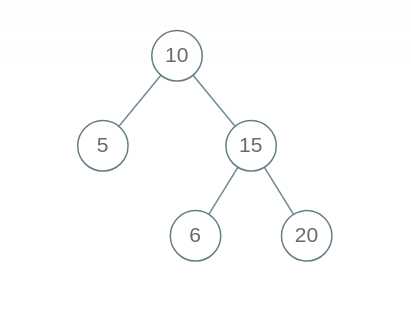
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
*/
function isValidBST(root) {
return isValidBST(root, null, null);
}
function isValidBST(root, min, max) {
if (root == null) return true;
if (min != null && root.val return false;
if (max != null && root.val >= max.val) return false;
return isValidBST(root.left, min, root)&& isValidBST(root.right, root, max);
}
3.二叉搜索树找值
function find(root,target) {
if(root==null)
return false
if(root.val==target)
//找到的操作
return true
return find(root.left,target)||find(root.right,target)
}
function find(root, target) {
if (root == null)
return false;
if (root.val == target)
return true;
if (root.val target)
return find(root.right, target);
if (root.val > target)
return find(root.left, target);
}
4. 二叉搜索树之查 框架
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
* @param {Number} target
*/
function BST(root, target) {
if (root.val == target)
// 找到目标,做点什么
if (root.val target)
BST(root.right, target);
if (root.val > target)
BST(root.left, target);
}
5. 二叉搜索树之增 框架
function insertIntoBST(root, val) {
// 找到空位置插入新节点
if (root == null)
return new TreeNode(val);
// if (root.val == val)
// BST 中一般不会插入已存在元素
if (root.val val)
root.right = insertIntoBST(root.right, val);
if (root.val > val)
root.left = insertIntoBST(root.left, val);
return root;
}
6. 二叉搜索树之删 框架
if (root.left == null && root.right == null)
return null;
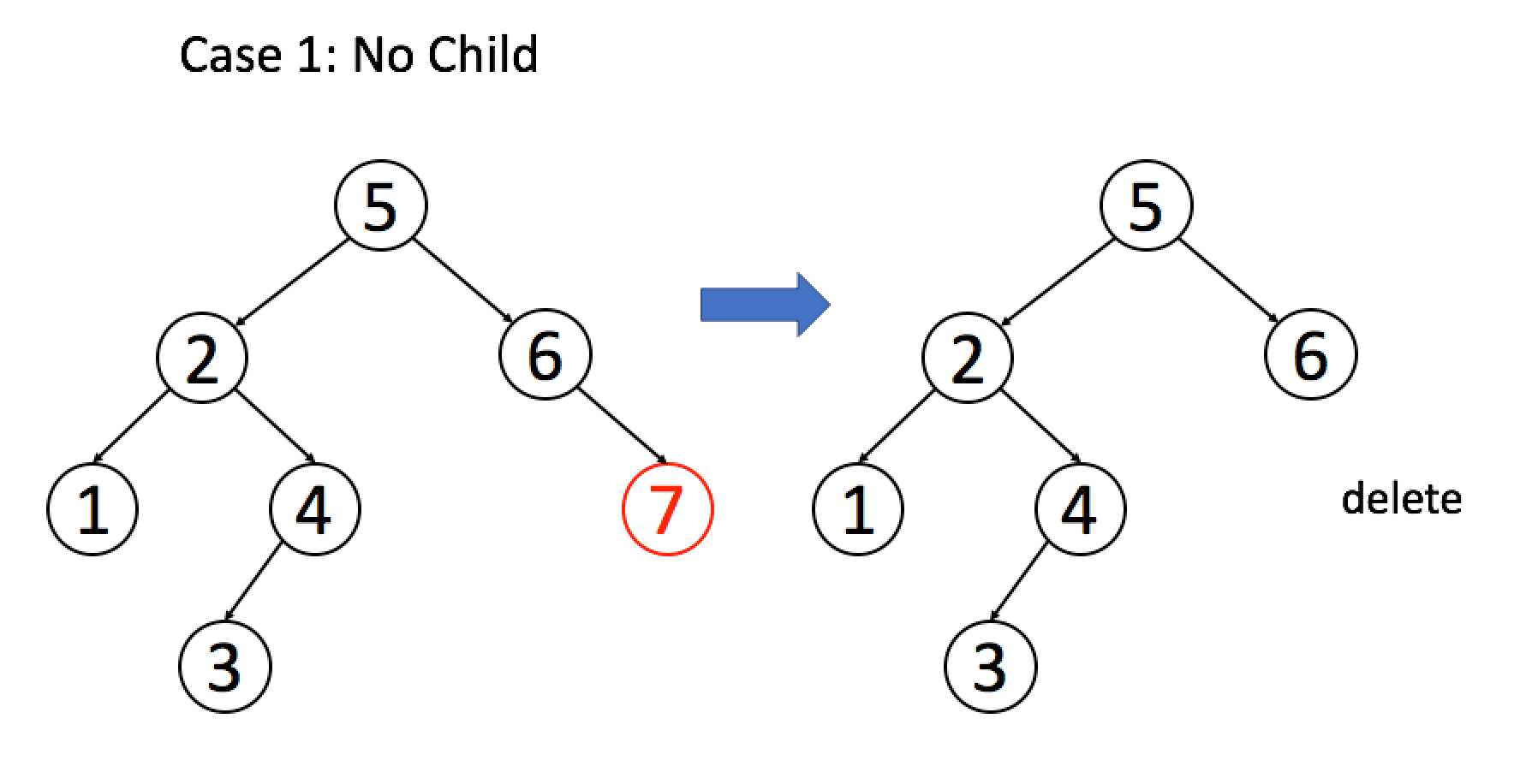
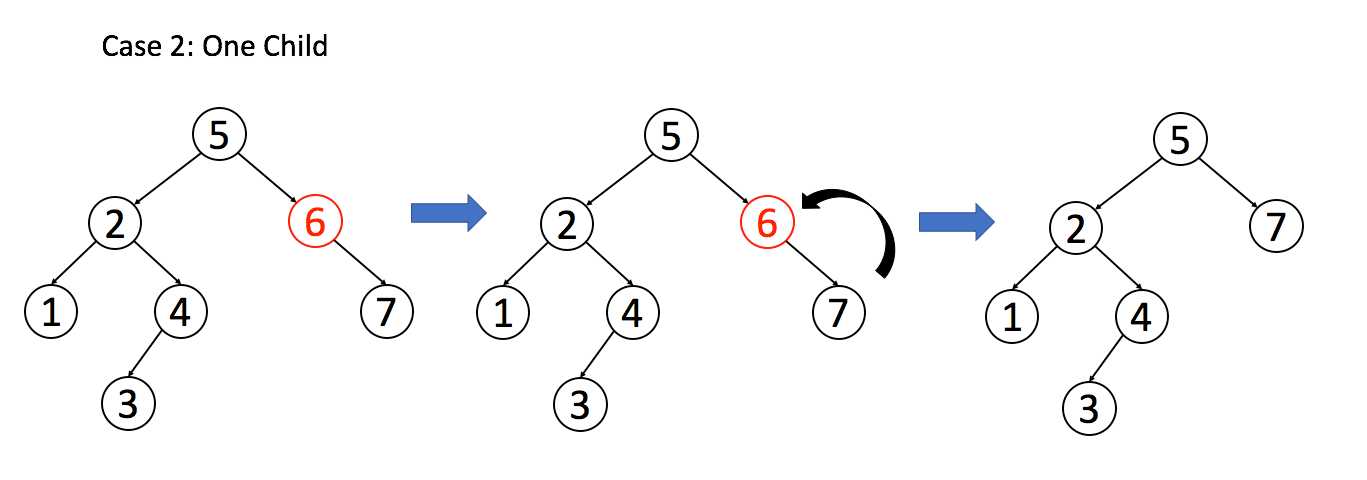
// 排除了情况 1 之后
if (root.left == null) return root.right;
if (root.right == null) return root.left;
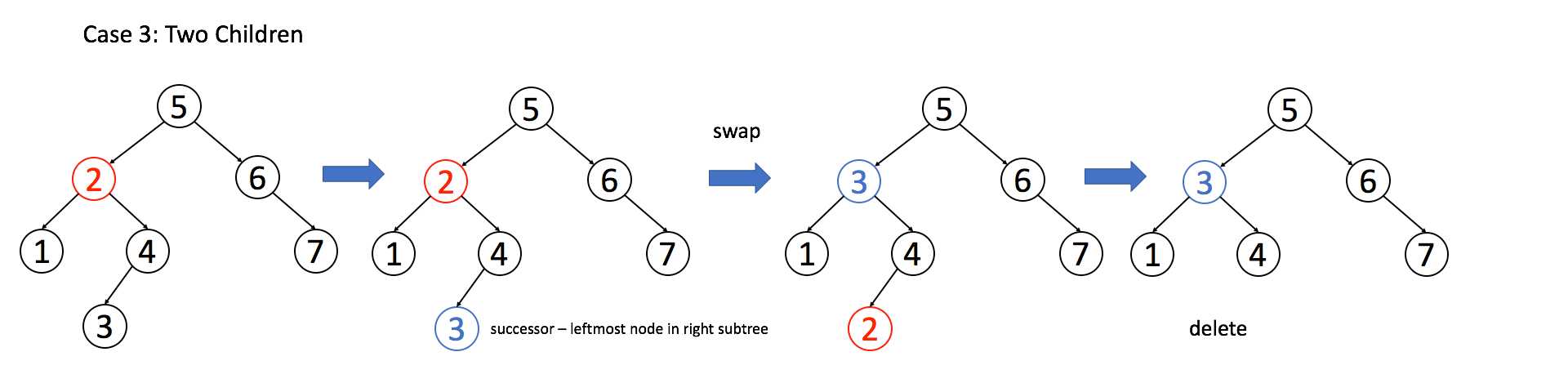
if (root.left != null && root.right != null) {
// 找到左子树的最大节点
var maxNode = getMax(root.left);
// 把 root 改成 maxNode
root.val = maxNode .val;
// 转而去删除 maxNode
root.left= deleteNode(root.left, maxNode.val);
}
function deleteNode(root, int key) {
if (root == null) return null;
if (root.val == key) {
// 这两个 if 把情况 1 和 2 都正确处理了
if (root.left == null)
return root.right;
if (root.right == null)
return root.left;
// 处理情况 3
var maxNode = getMax(root.left);
root.val = maxNode.val;
root.left= deleteNode(root.left, maxNode .val);
} else if (root.val > key) {
root.left = deleteNode(root.left, key);
} else if (root.val key) {
root.right = deleteNode(root.right, key);
}
return root;
}
//找左子树中的最大值【找左子树的最右下角的值】
function getMax(node) {
while (node.right!= null)
node = node.right;
return node;
}
下一篇:机器学习基础:SVM算法总结
文章标题:算法框架之二叉树扩展&二叉搜索树
文章链接:http://soscw.com/index.php/essay/49434.html