《Diffusion-ConvolutionalNeuralNetworks》论文阅读
2021-02-02 23:14
标签:无向图 http www 网络 图结构 src diff inline 基础上 下图展示过程应该更清晰: 上图就是需要输入的图结构以及节点的特征 对 \(v_{3}\)节点 进行一阶邻居【\((d(3,.)=1)\)】信息聚合,并同自己进行求 mean ,其中 \(w_3^{0}\) 就是对应的一阶的训练的 parameters。类似的,还需要处理其他的剩余节点。 类似的,hop 二阶。是在原图的基础上,而不是在已经经过一层的基础上处理 同理将距离变成二阶,就能一样聚合到二阶邻居信息。得到二阶,三阶... k阶 其中的矩阵就是对同一个node的一阶二阶...信息(文中称为diffusion) 以上过程应该蛮好理解的,可是论文其实可以写的更明白,可是参数和图示写的不怎么明白 其中graph可以是 带/不带 权重,有/无向图 我只以node-classification为例 通过矩阵表示则: 最后的分类,可适用argmax或者softmax(个人觉得可以全连接 或者 element-wise) 在node-classification上尚可,edge的实验却没做。实验在graph-classification上表现极差——因为我看作者通过将所有节点求和并平均了一下来表示graph-feature,着就让我想到了GNN上限的一篇论文,即sum的操作是优于mean的【当然对graph-classification了解不多,个人臆想】,mean反而更不容易区分开不同的graph了 这点没看懂,可能需要看更多论文来理解(ε=ε=ε=┏(゜ロ゜;)┛ GNN论文看的也不是很多,但是有个奇怪的想法,就是利用edge进行aggregate就算是利用了graph的structural-info 了吗? 【1】https://zhuanlan.zhihu.com/p/76669259 【2】https://media.nips.cc/nipsbooks/nipspapers/paper_files/nips29/reviews/1073.html 【3】https://www.youtube.com/watch?v=5eTJ6yxtU5s 【4】https://www.youtube.com/watch?v=eybCCtNKwzA 《Diffusion-ConvolutionalNeuralNetworks》论文阅读 标签:无向图 http www 网络 图结构 src diff inline 基础上 原文地址:https://www.cnblogs.com/KongHuZi/p/13166639.htmlDCNN
主要思想:
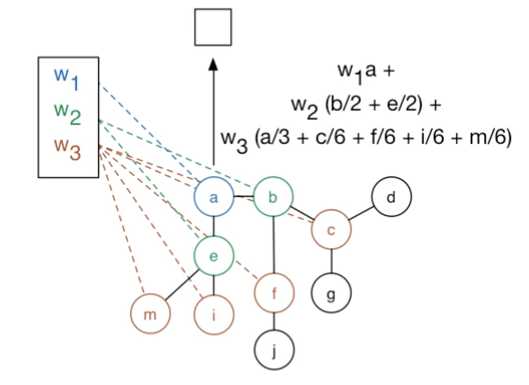
过程图示1
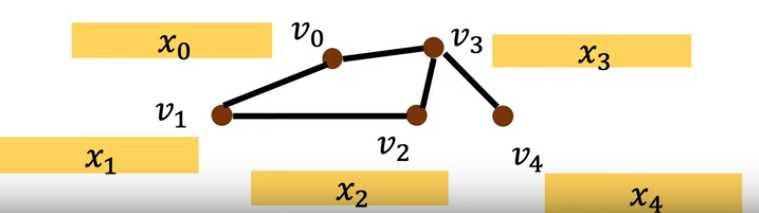

通过对5个节点分别进行处理,即经过一层 hidden-layer,输出结果为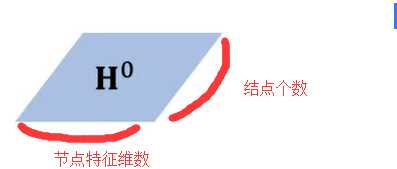

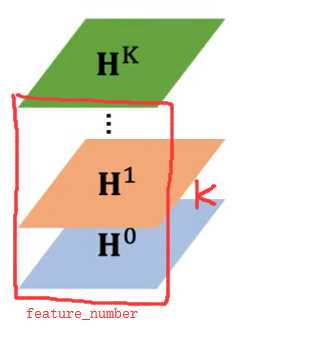
如果需要做一个节点分类,则将该矩阵拿出来,再同 \(w\) 进行 element-wise(or 全连接?) 即可,得到预测的分类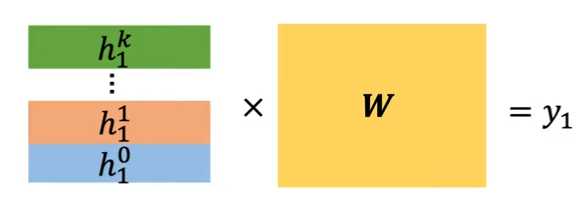
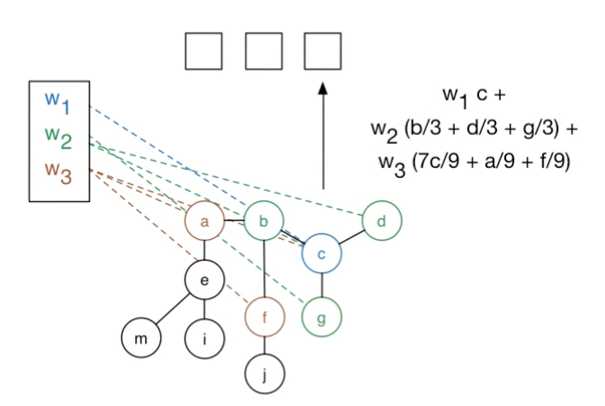
过程图示2
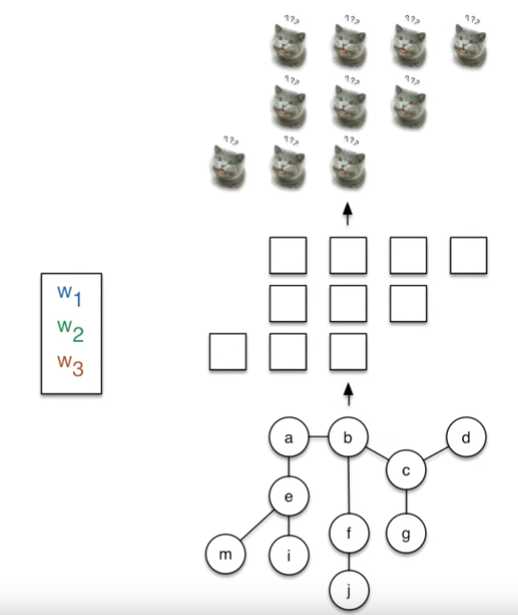
论文内容
PS 作者提出该DCNN 可适用于 node/graph/edge-classification,但是实验却只在node上表现还可以,graph上不行,edge甚至没做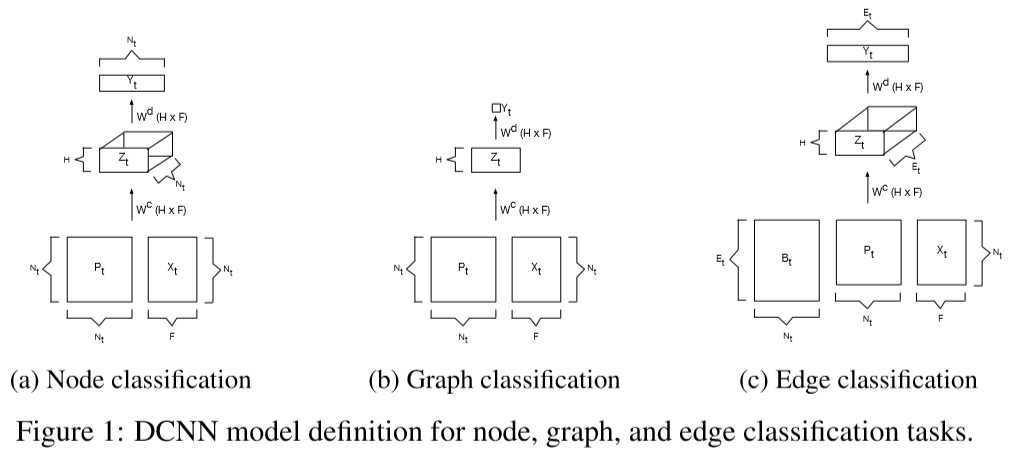
通过一次计算的公式: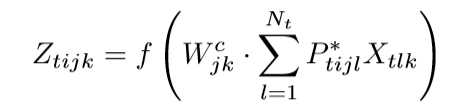
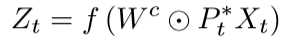
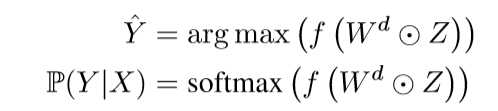
实验结果和缺点

杂谈
参考文献
上一篇:PHP 抽象类
文章标题:《Diffusion-ConvolutionalNeuralNetworks》论文阅读
文章链接:http://soscw.com/index.php/essay/50150.html