KM算法原理+证明
2021-02-06 20:17
标签：turn def over c++ 没有 ace mes 匈牙利算法 zsh title: KM算法原理+证明 以 百度百科中有KM算法的介绍，当中有证明过程：百度KM算法 带权二分图的边权重和最大的匹配，如下图所示，最大和为102 带权二分图的边权重和最大的完备匹配，如下图所示 显然，最佳匹配和最大权匹配并不一致，但如果把剩下的边补上，并且设置权重为零，那么二者可以统一起来 下面讲的KM算法是用来求最佳匹配，而非最大权匹配。 KM算法是一种计算机算法，功能是求完备匹配下的最大权匹配。 如果不存在完备匹配，那么算法会求最大匹配，如果最大匹配有多种，那么结果是最大匹配中权重和最大的。 在一个二分图内，左顶点为X，右顶点为Y，现对于每组左右连接XiYj有权，求最大匹配，并且使得该匹配中所有的和是最大。 该算法是通过给每个顶点一个标号（叫做顶标）来把求最大权匹配的问题转化为求完备匹配的问题的。 设顶点的顶标为的顶标为，顶点的顶标为，顶点与之间的边权为，在算法执行过程中，对于图中的任意一条边，始终成立。 G当中每一条边有左右两个顶标，*相等子图*就是那些顶标和等于边权重的边构成的子图，如下图绿色加粗线构成相等子图 KM算法的正确性基于以下的定理： 证明：因为这个完备匹配存在于相等子图中，因此，这个匹配所有边都满足：，同时由于完备匹配包含所有的顶点，因此这个属于相等子图的完备匹配的总权重等于所有顶标的和。 如果这个二分图存在另外一个完备匹配，如果它不完全属于相等子图，即存在某条边，那么该匹配的权重和就小于所有顶标的和，即小于上述属于相等子图的完备匹配的权重和。 首先选择顶点数较少的为X部，初始时对X部的每一个顶点设置顶标，顶标的值为该点关联的最大边的权值，Y部的顶点顶标为0。 对于X部中的每个顶点，在相等子图中利用匈牙利算法找一条增广路径，如果没有找到，则修改顶标，扩大相等子图，继续找增广路径。当每个点都找到增广路径时，此时意味着每个点都在匹配中，即找到了二分图的完备匹配。该完备匹配是最大权重的完备匹配，即为二分图的最佳匹配。 匈牙利算法对左边第一个顶点，在相等子图中进行增广路径搜索，找到路径1-C后进行匹配增广操作，如下图所示 回答第一个问题，需要理解如何在保持相等子图原来的边符合相等子图要求的同时，让新加的边也满足相等子图的要求。 那么在增广路径搜索时，我们知道，如果下面这些紫色边任意一条加入相等子图后，都可以在相等子图中使用匈牙利算法找到一条增广路径2-A（or 2-B or 2-C-1-A）： KM算法选择上述三条紫色边中，顶标和与边权重差值最小的边1-A或者2-A，以该最小差值为d 这里有一个问题就是为什么最小那个？首先比这更小了就不能扩大相等子图了，但是如果大了，就不能保证 而KM算法中需要修改的顶标，是那些在匈牙利算法增广路径搜索时，产生一棵交错树，为了保证 比如在如上第二个顶点搜索增广路径时，产生如下图所示的橙色顶标集合{1，2，C}： 修改顶标后产生如下图所示的结果： 在该相等子图上以顶点2为开始点，搜索增广路径2-A（or 2-C-1-A），进行增广操作: 同样对左边第三个点： 另外一个问题是为什么修改橙色顶标而不去修改顶标A（找到最小差对应的边的右边顶标）？修改顶标A的值为-1，那么边1-A也可以加入相等子图了。问题就在于能不能保证总是成立，如下图所示结果，修改顶标A，边3-A就不满足该条件了。除非在修改顶标A的同时，增加顶标3的值，但是需要修改的顶标集合需要额外的搜索算法，而修改橙色顶标所需要的交错树在增广路径搜索时可以一并产生。 KM算法原理+证明 标签：turn def over c++ 没有 ace mes 匈牙利算法 zsh 原文地址：https://www.cnblogs.com/sug-sams/p/12780580.html
date: 2020-04-26
categories: ["算法"]
summary: "以匈牙利算法为基础，改善后用于求解带权二分图的求最佳匹配问题。百度百科中有KM算法的介绍，当中有证明过程：[百度KM算法]"
author: White Song
tags: ["二分图"]
cover: https://img.yilon.top/blog/czsh9.png
blog: https://blog.yilon.top
介绍
匈牙利算法为基础，改善后用于求解带权二分图的求最佳匹配问题最大权匹配
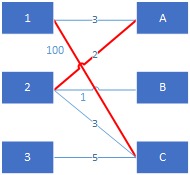
最佳匹配
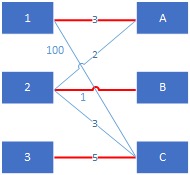
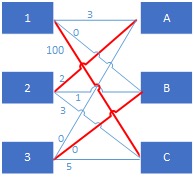
KM算法
相等子图
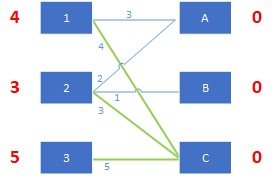
定理：若二分图中，，并且存在某个相等子图有完备匹配，那么这个完备匹配就是二分图的最大权匹配。算法过程
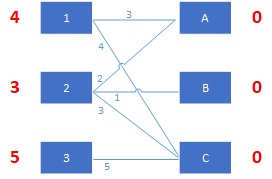
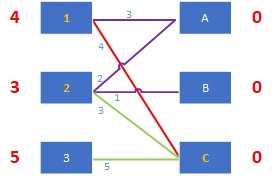
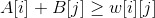总是成立了。比如上图选择了2-B边的差值2，那么修改顶标值后，1-A有
。
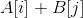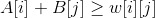总是成立，交错树上所有的顶标都要参与修改。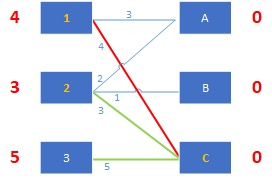
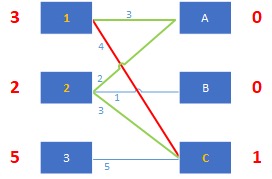
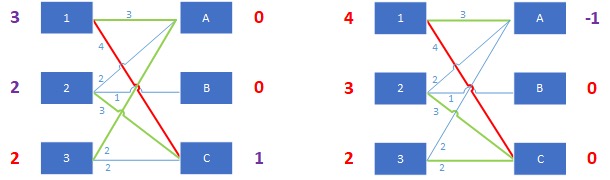
C++代码
#include