数据结构与算法-赫夫曼树

标签：move   实际应用   err   ring   它的   布尔   import   最小   遍历   

树的实际应用-赫夫曼树

1. 基本介绍

• 给定 n 个权值作为 n 个叶子结点，构造一棵二叉树，若该树的带权路径长度（wpl）达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树（Huffman Tree），也称霍夫曼树
• 赫夫曼树是带权路径长度最短的树，权值较大的结点离根较近

2. 重要概念

• 路径和路径长度：在一颗树中，从一个结点往下可以达到的孩子或孙子结点之间的通路，称为路径。通路中分支的数目称为路径长度。若规定根结点的层树为1，则从根结点到第L层结点的路径长度为 L-1
• 结点的权：若将树中结点赋给一个有某种含义的数值，则这个数值称为该结点的权。
• 结点的带权路径长度：从根结点到该结点之间的路径长度与该结点的权的乘机
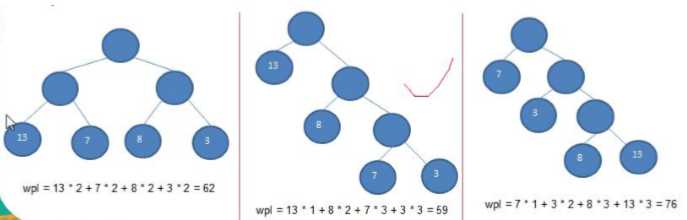
• 树的带权路径长度：树的带权路径长度规定为所有叶子结点的带权路径长度之和，记为WPL，权值越大的结点离根结点越近的二叉树才是最优二叉树
• WPL最小的就是赫夫曼树

3. 创建思路

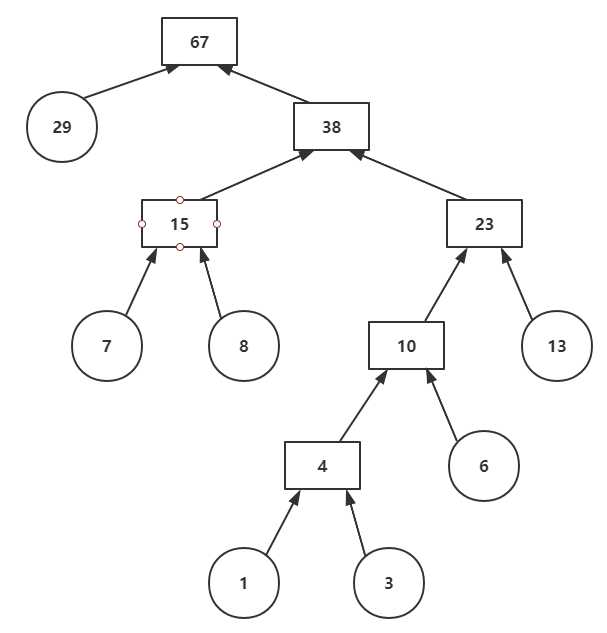
{13， 7， 8， 3， 29， 6， 1}，要求转成一颗赫夫曼树

步骤

• 从小到大进行排序，每一个数据都是一个结点，每个结点可以看成是一颗最简单的二叉树
• 取出根结点权值最小的两颗二叉树
• 组成一颗新的二叉树，该新的二叉树的根结点的权值是前面两颗二叉树根结点权值的和
• 再将这颗新的二叉树，以根结点的权值大小再次排序，不断重复 此步骤，直到数列中，所有的数据都被处理，就得到一颗赫夫曼树

4. 代码实现

package cn.imut;

import java.util.ArrayList;
import java.util.Collections;
import java.util.List;

public class HuffmanTree {
    public static void main(String[] args) {
        int[] arr = {13, 7, 8, 3, 29, 6, 1};
        Node root = createHuffmanTree(arr);
        preOrder(root);
    }

    //前序遍历
    public static void preOrder(Node root) {
        if(root != null) {
            root.preOrder();
        }else {
            System.out.println("是空树，不能遍历~");
        }
    }

    //创建赫夫曼树

    /**
     *
     * @param arr 需要创建成哈夫曼树的数组
     * @return 创建好赫夫曼树的root结点
     */
    public static Node createHuffmanTree(int[] arr) {
        //将元素构成Node，放入ArrayList
        List nodes = new ArrayList();
        for (int value : arr) {
            nodes.add(new Node(value));
        }

        while (nodes.size() > 1) {
            Collections.sort(nodes);
            System.out.println("nodes = " + nodes);

            //取出根结点最小的两颗二叉树
            //1.取出权值最小的结点
            Node leftNode = nodes.get(0);
            //2.取出权值第二小的结点
            Node rightNode = nodes.get(1);
            //3.构建一颗新的二叉树
            Node node = new Node(leftNode.value + rightNode.value);
            node.left = leftNode;
            node.right = rightNode;
            //4.从ArrayList删除处理过的二叉树
            nodes.remove(leftNode);
            nodes.remove(rightNode);
            //5.将node加入到nodes
            nodes.add(node);
        }
        //返回赫夫曼树的root结点
        return nodes.get(0);
    }
}

//结点
/*
    Comparable接口强行对实现它的类的每个实例进行自然排序
    该接口的唯一方法compareTo方法被称为自然比较方法；
    强烈建议自然排序和equals一致（就是两个对象调用compareTo方法和调用equals方法返回的布尔值应该一样）
 */
class Node implements Comparable{

    int value;  //结点权值
    Node left;  //指向左子结点
    Node right; //指向右子结点

    //前序遍历
    public void preOrder() {
        System.out.println(this);

        if (this.left != null) {
            this.left.preOrder();
        }
        if (this.right != null) {
            this.right.preOrder();
        }
    }
    public Node(int value) {
        this.value = value;
    }

    @Override
    public String toString() {
        return "Node{" +
                "value=" + value +
                ‘}‘;
    }

    @Override
    public int compareTo(Node o) {
        //表示从小到大排序
        return this.value -o.value;
    }
}

数据结构与算法-赫夫曼树

标签：move   实际应用   err   ring   它的   布尔   import   最小   遍历   

原文地址：https://www.cnblogs.com/yfyyy/p/12769526.html