5.线性回归算法
2021-02-10 16:19
标签:异常 代码 机器学习 预测 等等 format read 曲线 关系 1.本节重点知识点用自己的话总结出来,可以配上图片,以及说明该知识点的重要性 1)。机器学习算法中回归算法的分类 2)。回归与分类的区别 3)线性回归的定义 线性回归模型建模速度快,不需要很复杂的计算,在数据量大的情况下依然运行速度很快;可以根据系数给出每个变量的理解和解释;对异常值很敏感。 线性回归,它不仅仅是一维;它可以是多维的;可以是曲线;亦可直线;甚至可达更高维;等等。 4)线性模型: 5)线性回归的损失 任何一件事的过程都有一定的误差,预测也不例外,而这个范围称为最小二乘法。 6)明确线性回归算法的缺点,并对其进行优化。 7).本章主要内容总结 8)本章所运用到的代码: 1)。面积与房价的关系 2).数组的点乘和矩阵的乘积。 3).手写线性回归方程,并计算其损失值 2.思考线性回归算法可以用来做什么?(大家尽量不要写重复) 线性回归算法可以用来做:全国快递运输总量预测,股价走势预测,人们收入增长预测,中国人口增长分析等等。 3.自主编写线性回归算法 ,数据可以自己造,或者从网上获取。(加分题) 分析产品A的单价与销量之间的关系,来预测当产品A的定价为x,市场的需求量y将会是多少,就能知道该向供应商订购多少产品A。 截图: 5.线性回归算法 标签:异常 代码 机器学习 预测 等等 format read 曲线 关系 原文地址:https://www.cnblogs.com/a131452/p/12742075.html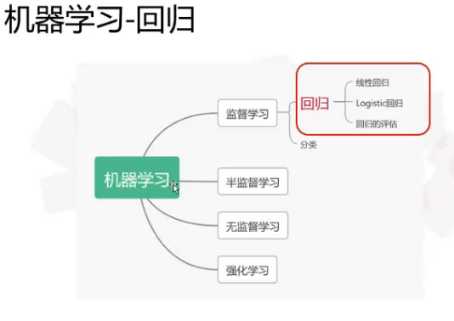







import matplotlib.pyplot as plt
plt.figure(figsize=(5, 5))
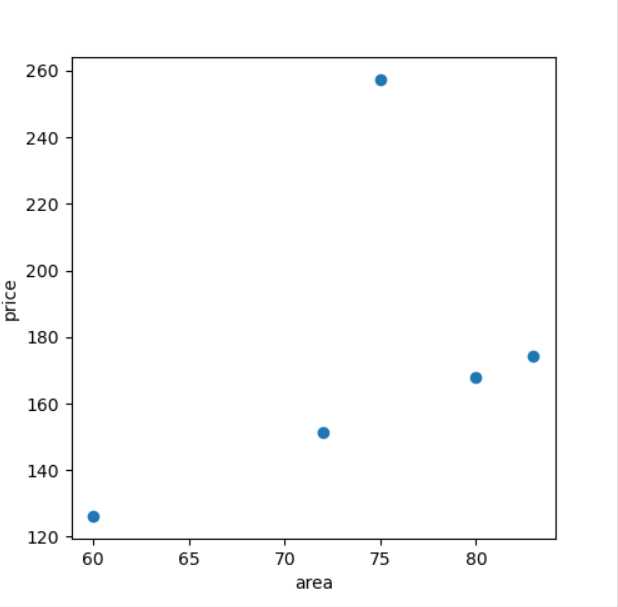
plt.scatter([60, 72, 75, 80, 83], [126, 151.2, 257.5, 168, 174.3])
plt.xlabel("area")
plt.ylabel("price")
plt.show()
import numpy as np
a = [[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]]
b = [1, 2, 3, 4]
c = np.multiply(a, b)
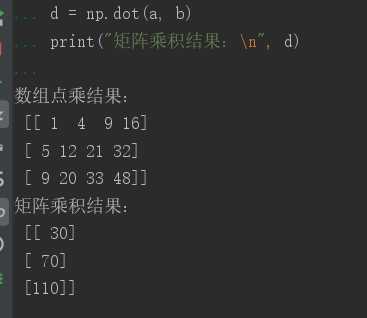
print("数组点乘结果:\n", c)
b = [[1], [2], [3], [4]]
d = np.dot(a, b)
print("矩阵乘积结果:\n", d)
import random
import matplotlib.pyplot as plt
x = [0.1*x for x in range(0, 10)]
y = [12*i*4 for i in x]
print(x)
print(y)
w = random.random()
b = random.random()
a1 = []
b1 = []
for i in range(10):
for x1, y1 in zip(x, y):
o = w*x1+b # 预测值
e = (o-y1)
loss = e**2 # 损失值
dw = 2*e*x1
db = 2*e*1
w = w-0.1*dw
b = b-0.1*db
print(‘loss={0},w={1},b={2}‘. format(loss, w, b))
# loss越小越好
a1.append(i)
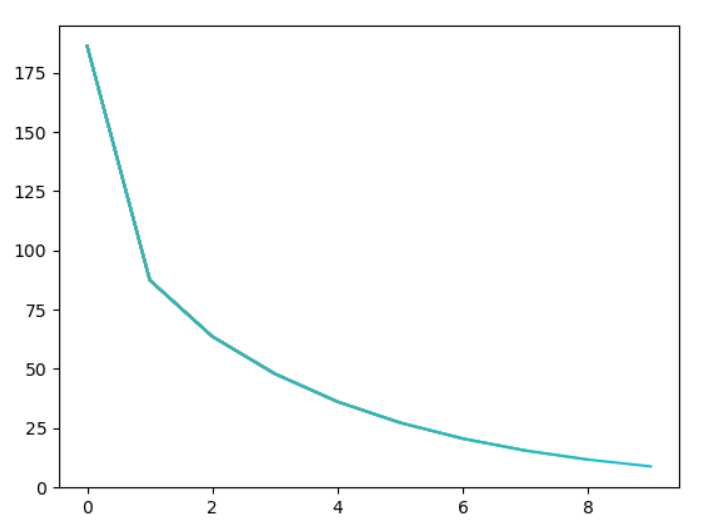
b1.append(loss)
plt.plot(a1, b1)
plt.pause(0.1)
plt.show()
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
df = pd.read_csv(‘price_demand.csv‘)
# print(df[[‘Price‘]])
x = df[‘Price‘]
# print(x)
y = df[‘Demand‘]
x_mean = np.mean(x)
y_mean = np.mean(y)
num = 0
dom = 0
for x1, y1 in zip(x, y):
num += (x1-x_mean)*(y1-y_mean)
dom += (x1-x_mean)**2
a = num/dom
b = y_mean-a*x_mean
# 预测值
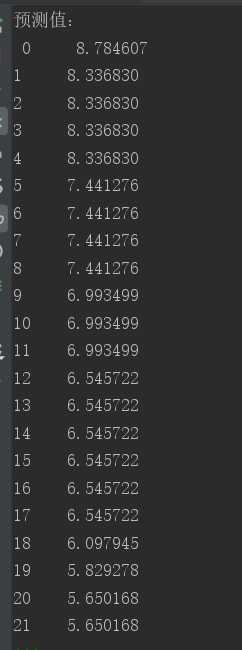
y_pred = a*x+b
print(‘预测值:\n‘, y_pred)
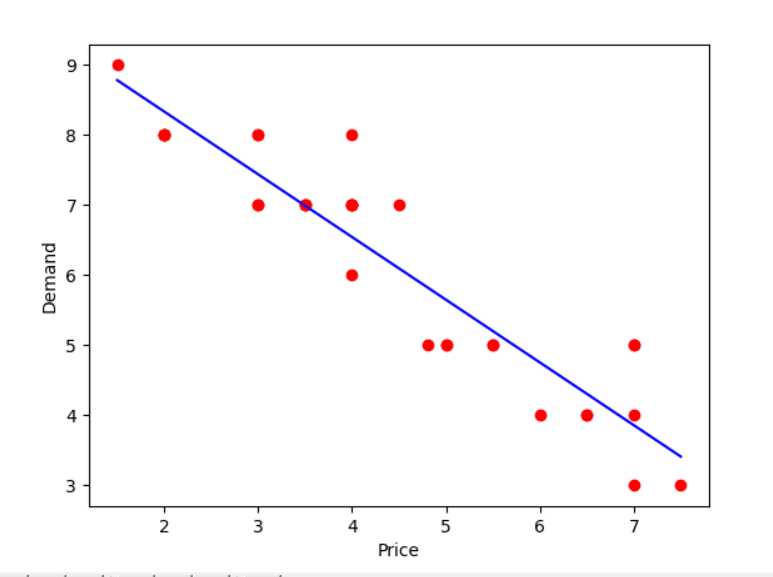
# 可视化
plt.scatter(x, y, color=‘red‘) # 样本点
plt.plot(x, y_pred, color=‘blue‘) # 蓝色回归线
plt.xlabel("Price")
plt.ylabel("Demand")
plt.show()