试题 算法训练 奇异的虫群 -> 矩阵快速幂
2021-02-10 16:20
#includeusing namespace std; const int mod = 1000000007; typedef long long ll; int main() { ll n; cin >> n; ll a = 1; ll b = 1; ll ans = 1; for (int i = 2; i ) { int temp = a; a = (a % mod + b % mod) % mod; b = temp; } cout endl; return 0; }
// 超时代码
这里我们先引入复习一下快速幂模板
#includeusing namespace std; typedef long long ll; ll mul(ll a, ll b, ll p) { ll ans = 1; while (b) { if (b & 1) ans = ans * a % p; a = a * a % p; b >>= 1; } return ans ; } int main() { ll a, b, p; cin >> a >> b >> p; cout endl; return 0; }
这里贴上新学习的矩阵快速幂的模板
个人认为比较好理解一些
#include#include #include #include using namespace std; typedef long long ll; const int N = 105, mod = 1000000007; int n; ll k; struct Mat { ll a[N][N]; // longlong存矩阵 否则过程中会爆掉 Mat() { memset(a, 0, sizeof a); } inline void build() //建造单位矩阵 { for (int i = 1; i 1; } }mat; Mat operator * (const Mat &x, const Mat &y) //重载运算符 { Mat z; for (int k = 1; k ) for (int i = 1; i ) for (int j = 1; j ) z.a[i][j] = (z.a[i][j] + x.a[i][k] * y.a[k][j] % mod) % mod; return z; } int main() { cin >> n >> k; for (int i = 1; i ) for (int j = 1; j ) cin >> mat.a[i][j]; Mat ans; ans.build(); // 实际相当于求快速幂中ans=1 这里ans为矩阵 所以初始化为单位矩阵 while (k) { if (k & 1) ans = ans * mat; mat = mat * mat; k >>= 1; } for (int i = 1; i ) { for (int j = 1; j ) cout ‘ ‘; cout endl; } return 0; }
在求斐波那契数列 可以使用矩阵快速幂
矩阵快速幂是用来求解递推式的,所以第一步先要列出递推式:
f(n)=f(n-1)+f(n-2)
第二步是建立矩阵递推式,找到转移矩阵:
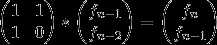 ,简写成T * A(n-1)=A(n),T矩阵就是那个2*2的常数矩阵,而
,简写成T * A(n-1)=A(n),T矩阵就是那个2*2的常数矩阵,而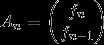
这里就是个矩阵乘法等式左边:1*f(n-1)+1*f(n-2)=f(n);1*f(n-1)+0*f(n-2)=f(n-1);
所以这里相乘就是矩阵n-1次相乘,然后输出第一行第二个元素,也就是a[0][1];
把第一个矩阵设为A,第二个矩阵设为B,第三个矩阵设为C。
总而言之 :最终斐波那契数列可以从矩阵中对应此公式
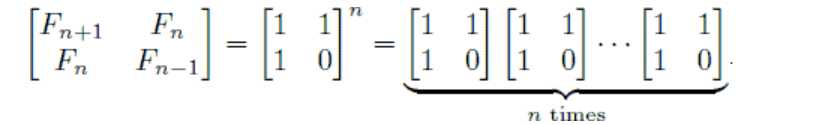
由 F2 F1 F1 F0 组成的矩阵的n次方 的左下角就是Fn。
所以可以上代码
注:此题和标准的斐波那契数列(1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, ...)有不同处
标准的即f0=0,f1=1,f2=1,f3=2 而此题中f1=1,f2=2
所以我们最后实则应该求f的n+1项
#include#include #include #include using namespace std; typedef long long ll; const int mod = 1000000007; ll n, k; struct Mat { ll a[2][2]; Mat() { memset(a, 0, sizeof a); } inline void build() { for (int i = 0; i 2; i ++ ) a[i][i] = 1; } }base; Mat operator * (const Mat &x, const Mat &y) { Mat z; for (int k = 0; k 2; k ++ ) for (int i = 0; i 2; i ++ ) for (int j = 0; j 2; j ++) z.a[i][j] = (z.a[i][j] + x.a[i][k] * y.a[k][j] % mod) % mod; return z; } int main() { cin >> n; base.a[0][0] = 1, base.a[0][1] = 1, base.a[1][0] = 1, base.a[1][1] = 0; //将base初始化为要求n次幂的矩阵 Mat ans; ans.build(); while (n) { if (n & 1) ans = ans * base; base = base * base; n >>= 1; } cout 0][0] endl; // cout return 0; }
上一篇:线程基础,JavaSE部分
下一篇:流畅的python学习1
文章标题:试题 算法训练 奇异的虫群 -> 矩阵快速幂
文章链接:http://soscw.com/index.php/essay/53650.html