最小生成树算法
2021-02-10 22:17
标签:weight next 排列 += des width 规模 kruskal算法 整数 最小生成树介绍: 修路问题本质就是最小生成树问题,先介绍一下最小生成树(Minimum Cost Spanning Tree),简称MST。 1)给定一个带权的无向连通图,如何选择一颗生成树,使树上所有边上权的总和为最小,这叫最小生成树。 2)N个顶点,一定有N-1条边 3)包含全部顶点 4)N-1条边都在图中 5)求最小生成树的算法主要是Prim算法和Kruskal算法 Prim算法 应用场景---修路问题 正确思路:尽可能的选择少的路线,并且每条路线最小,从而保证总里程数最小 Prim算法介绍: 1)Prim算法求最小生成树,也就是在包含n个顶点的连通图中,找出只有(n-1)条边包含所有n个顶点的连通子图,也就是所谓的极小连通子图 2)Prim算法如下: (1)设G = (V,E)是连通网,T = (U,D)是最小生成树,V,U是顶点集合,E、D是边的集合 (2)若从顶点u开始构造最小生成树,则从集合V中取出顶点u放入集合U中,标记顶点v的visited[u] = 1 (3)若集合U中顶点ui与集合V-U中的顶点vj之间存在边,则寻找这些边中权值最小的边,但不能构成回路,将顶点vj加入集合U中,将边(ui,vj)加入集合D中,标记visited[vj] = 1 (4)重复步骤2),直到U与V相等,即所有顶点都被标记为访问过,此时D中有n-1条边 给个例题理解一下: Kruskal算法 应用场景---公交站问题 Kruskal算法介绍: 1)是用来求加权连通图的最小生成树算法 2)基本思想:按照权值从小到大的顺序选择n-1条边,并保证这n-1条边不构成回路 3)具体做法:首先 构造一个只含n个顶点的森林,然后依权值从小到大从连通网中选择边加入到森林中,并使森林中不产生回路,直至森林变成一棵树为止 Kruskal算法重点需要解决的两个问题: 问题一 对图的所有边按照权值大小进行排序 问题二 将边添加到最小生成树中时,怎么样判断是否形成了回路 问题一很好解决,采用排序算法进行排序即可 问题二,处理方式是:记录顶点在“最小生成树”中的终点,顶点的终点是“在最小生成树中与它连通的最大顶点”。然后每次需要将一条边添加到最小生成树时,判断该边的两个顶点的终点是否重合,重合的话则会构成回路。 关于终点的说明: 1) 就是将所有顶点按照从小到大的顺序排列(单纯指的就是顶点的大小)好之后,某个顶点的终点就是“与它连通的最大顶点”。 2) 判断回路的方式。我们加入的边的两个顶点不能都指向同一个终点,否则将构成回路。 下面的“边”类仅供参考。 最小生成树算法 标签:weight next 排列 += des width 规模 kruskal算法 整数 原文地址:https://www.cnblogs.com/AIchangetheworld/p/12741278.html

1 问题描述
2
3 2015年,全中国实现了户户通电。作为一名电力建设者,小明正在帮助一带一路上的国家通电。
4 这一次,小明要帮助 n 个村庄通电,其中 1 号村庄正好可以建立一个发电站,所发的电足够所有村庄使用。
5 现在,这 n 个村庄之间都没有电线相连,小明主要要做的是架设电线连接这些村庄,使得所有村庄都直接或间接的与发电站相通。
6 小明测量了所有村庄的位置(坐标)和高度,如果要连接两个村庄,小明需要花费两个村庄之间的坐标距离加上高度差的平方,形式化描述为坐标为 (x_1, y_1) 高度为 h_1 的村庄与坐标为 (x_2, y_2) 高度为 h_2 的村庄之间连接的费用为
7 sqrt((x_1-x_2)(x_1-x_2)+(y_1-y_2)(y_1-y_2))+(h_1-h_2)*(h_1-h_2)。
8 在上式中 sqrt 表示取括号内的平方根。请注意括号的位置,高度的计算方式与横纵坐标的计算方式不同。
9 由于经费有限,请帮助小明计算他至少要花费多少费用才能使这 n 个村庄都通电。
10
11 输入格式
12
13 输入的第一行包含一个整数 n ,表示村庄的数量。
14 接下来 n 行,每个三个整数 x, y, h,分别表示一个村庄的横、纵坐标和高度,其中第一个村庄可以建立发电站。
15
16 输出格式
17
18 输出一行,包含一个实数,四舍五入保留 2 位小数,表示答案。
19
20 样例输入
21
22 4
23 1 1 3
24 9 9 7
25 8 8 6
26 4 5 4
27
28 样例输出
29
30 17.41
31
32 评测用例规模与约定
33
34 对于 30% 的评测用例,1 ;
35 对于 60% 的评测用例,1 ;
36 对于所有评测用例,1


1 import java.util.Scanner;
2
3 public class Main {
4 static class Node {
5 int x;
6 int y;
7 int h;
8 }
9
10 public static void main(String[] args) {
11 //输入
12 Node[] nodes = new Node[1002];
13
14 Scanner sc = new Scanner(System.in);
15 int n = sc.nextInt();
16 for (int i = 1; i ) {
17 nodes[i]=new Node();
18 nodes[i].x = sc.nextInt();
19 nodes[i].y = sc.nextInt();
20 nodes[i].h = sc.nextInt();
21 }
22 sc.close();
23 //初始化数组
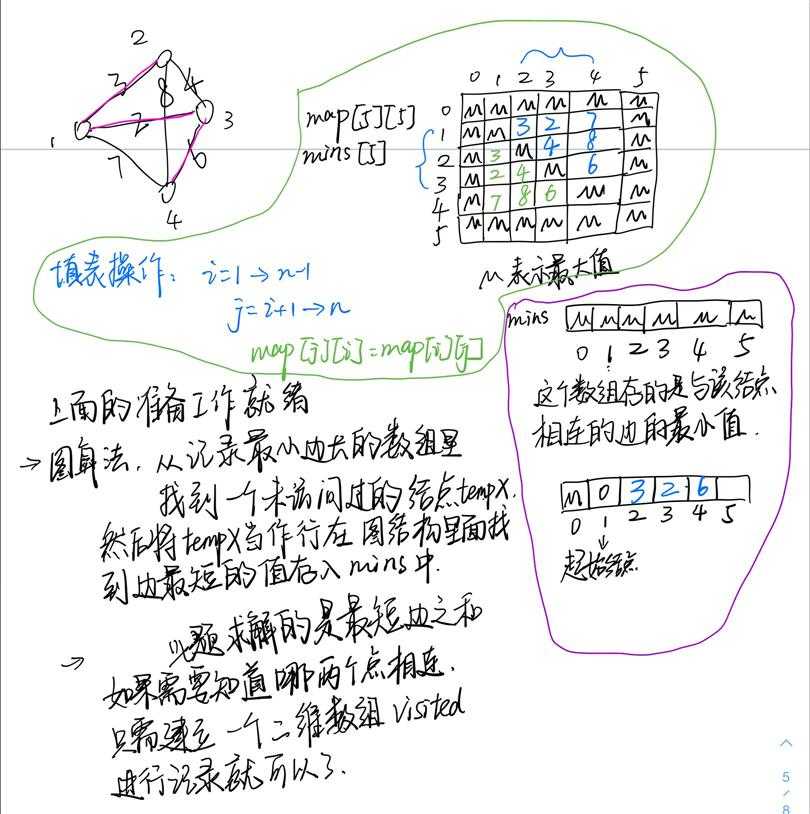
24 double[][] map = new double[n + 2][n + 2];
25 double[] mins = new double[n + 2]; //这个最后是用来保存最小值的
26 double MAX = 0x7f7f7f7f;
27 for (int i = 0; i ) {
28 for (int j = 0; j ) {
29
30
31 map[i][j]=MAX;
32
33 }
34 mins[i] = MAX;
35 }
36 //先找到每个值的最短路
37
38 for (int i = 1; i ) {
39 for (int j = i + 1; j ) {
40 double x = (nodes[i].x - nodes[j].x) * (nodes[i].x - nodes[j].x);
41 double y = (nodes[i].y - nodes[j].y) * (nodes[i].y - nodes[j].y);
42 double h = (nodes[i].h - nodes[j].h) * (nodes[i].h - nodes[j].h);
43 double temp=Math.sqrt(x+y)+h;
44 map[i][j]=Math.min(map[i][j],temp );
45 map[j][i]=map[i][j];
46 }
47 }
48 //然后图算法公式
49 boolean[] vis = new boolean[n+2];
50 mins[1]=0;
51 for (int i = 1; i


1 //该类EData 的对象实例就表示一条边
2 class EData{
3 char start;//边的一个点
4 char end;//边的另外一个点
5 int weight;//边的权值
6 public EData(char start,char end,int weight){
7 this.start = start;
8 this.end = end;
9 this.weight = weight;
10 }
11
12 //重写 toString ,便于输出
13 public String toString(){
14 return "EData[ = "+weight+"]";
15 }
16 }