Dijkstra算法（原理及python,c++实现）

2021-02-12 14:19

阅读：404

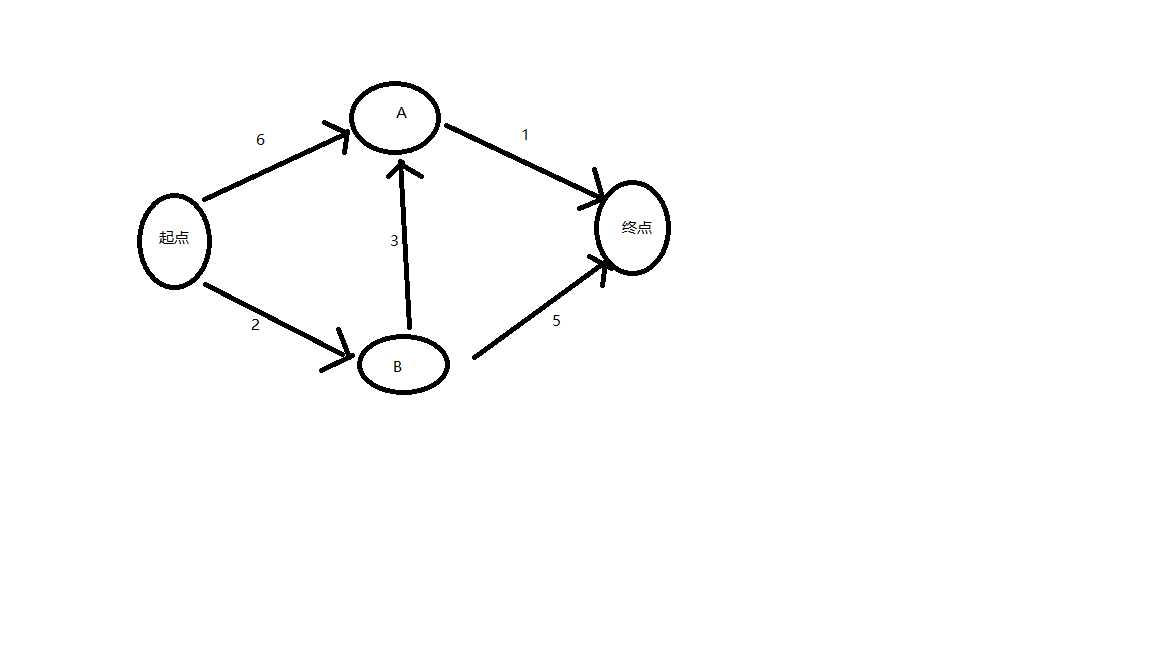
标签：初始 uil ESS 最小花费 tar 结束 app png 起点

原理及python实现

graph：保存图，类似邻接表

costs：保存从起点到某点的最小花费

parents：保存节点的父节点

processed：用于保存已经处理过的点

graph={}
graph["start"]={}
graph["start"]["a"]=6
graph["start"]["b"]=2
graph["b"]={}
graph["b"]["a"]=3
graph["b"]["fin"]=5
graph["a"]={}
graph["a"]["fin"]=1
graph["fin"]={}
infinity=float("inf")
costs={}
costs["a"]=6
costs["b"]=2
costs["fin"]=infinity
parents={}
parents["a"]="start"
parents["b"]="start"
parents["fin"]=None
processed=[]
def find_lowest_cost_node(costs):#找出还未处理过的花费最小的点
    lowest_cost=float("inf")
    lowest_cost_node=None
    for node in costs:
        cost = costs[node]
        if cost and node not in processed:
            lowest_cost=cost
            lowest_cost_node=node
    return lowest_cost_node
node=find_lowest_cost_node(costs)
while node is not None:#这个while循环在所有节点都被处理过后结束
    cost=costs[node]
    neighbors=graph[node]
    for n in neighbors.keys():#遍历当前节点的所有邻居
        new_cost=cost+neighbors[n]
        if costs[n]>new_cost:#如果进过当前节点前往该邻居更近
            costs[n]=new_cost#就更新该邻居的开销
            parents[n]=node#并将该邻居的父节点设置为当前节点
    processed.append(node)#将当前节点标记为处理过
    node=find_lowest_cost_node(costs)#找出接下来要处理的节点，并循环
print(costs[‘fin‘])

c++实现

#includeusing namespace std;
const int inf=1e6;
const int num=105;
struct edge{
    int from,to,w;
    edge(int a,int b,int c){from=a,to=b,w=c;}
};
vectore[num];//用邻接表纯图 

struct costs_node{
    int id,cost;
    costs_node(int b,int c){id=b,cost=c;}
    bool operatorconst costs_node & a) const
    {return cost>a.cost;} //优先队列花费小的节点先出队 
};
priority_queueQ;
int dis[num],vis[num]={0},fa[num];
void build(){//创建图 
    while(!Q.empty())Q.pop();
    e[0].push_back(edge(0,1,6));
    e[0].push_back(edge(0,2,2));
    e[1].push_back(edge(1,3,1));
    e[2].push_back(edge(2,3,5));
    e[2].push_back(edge(2,1,3));
    fa[1]=0;
    fa[2]=0;
    fa[3]=inf;
    dis[1]=6;//将起点的邻居节点初始化 
    dis[2]=2;
    Q.push(costs_node(1,6));
    Q.push(costs_node(2,2));
    Q.push(costs_node(3,inf));
} 
void print_path(int s,int t){//输出路径 
    if(s==t){
        printf("%d",s);return;
    }
    print_path(s,fa[t]);
    printf("%d",t);
}
void Dijkstra(){
    int s=0;
    for(int i=0;i3;i++){
        dis[i]=inf;
        vis[i]=false;
    }
    dis[0]=0;
     build(); 
    while(!Q.empty()){
        costs_node u=Q.top();
        Q.pop();
        if(vis[u.id])continue;
        vis[u.id]=1;
        for(int i=0;i){
            edge y=e[u.id][i];
            if(vis[y.to])continue;
            if(dis[y.to]>y.w+u.cost){
                dis[y.to]=y.w+u.cost;
                Q.push(costs_node(y.to,dis[y.to]));
                fa[y.to]=u.id;
            }
        }
    }
    printf("%d\n",dis[3]); 
    print_path(s,3);//输出路径 
}
int main(){
    Dijkstra();
}