数据结构和算法(Golang实现)(15)常见数据结构-列表
2021-02-13 22:19
标签:缓存数据库 信息 接口 就是 链接 使用 red val 数据结构和算法 我们又经常听到 列表 我们一般写算法进行数据计算,数据处理,都需要有个地方来存数据,我们可以使用封装好的数据结构 列表的实现有 顺序表示:指的是用一组 链式表示:指的是用一组 我们在前面已经实现过这两种表示的数据结构:先进先出的 双端列表,也可以叫双端队列 我们会用双向链表来实现这个数据结构: 设计结构体 我们实现的双端列表和 以上是对节点结构体 首先加锁实现并发安全。然后判断索引是否超出列表长度: 如果 首先,找出头部: 接着初始化新节点: 定位到的节点有三种情况,我们需要在该节点之前插入新节点: 判断定位到的节点 否则找到定位到的节点的前驱节点: 如果前驱节点为空: 新节点成为新的头部,需要将新节点的后驱设置为老头部: 如果定位到的节点的前驱节点不为空,表明定位到的节点 先将定位到的节点的前驱节点和新节点绑定,因为现在新节点插在前面了,把定位节点的前驱节点的后驱设置为新节点: 同时,定位到的节点现在要链接到新节点之后,所以新节点的后驱设置为: 最后,链表长度加一。 大部分时间花在遍历位置上,如果 操作和头部插入节点相似,自行分析。 如果索引超出或等于列表长度,那么找不到节点,返回空。 否则从头部开始遍历,拿到节点。 时间复杂度为: 操作和从头部获取节点一样,请自行分析。 首先加并发锁实现并发安全。先判断索引是否超出列表长度: 获取头部,然后遍历定位到第 定位到的并要移除的节点有三种情况发生: 查看要移除的节点的前驱和后驱: 如果前驱和后驱都为空: 如果前驱节点为空: 同理,如果后驱节点为空: 如果移除的节点处于两个节点之间,那么将这两个节点链接起来即可: 最后,列表长度减一。 主要的耗时用在定位节点上,其他的操作都是链表链接,可以知道时间复杂度为: 操作和从头部移除节点相似,请自行分析。 输出: 首先,先从列表头部插入三个新元素,然后从尾部插入两个新元素,然后用三种方式进行遍历,两种只是查看元素,一种是遍历移除元素。 我是陈星星,欢迎阅读我亲自写的 数据结构和算法(Golang实现),文章首发于 阅读更友好的GitBook。 数据结构和算法(Golang实现)(15)常见数据结构-列表 标签:缓存数据库 信息 接口 就是 链接 使用 red val 数据结构和算法 原文地址:https://www.cnblogs.com/nima/p/12724834.html列表
一、列表 List
列表 List数据结构,其实这只是更宏观的统称,表示存放数据的队列。
List:存放数据,数据按顺序排列,可以依次入队和出队,有序号关系,可以取出某序号的数据。先进先出的队列 (queue)和先进后出的栈(stack)都是列表。大家也经常听说一种叫线性表的数据结构,表示具有相同特性的数据元素的有限序列,实际上就是列表的同义词。List:顺序表示或链式表示。地址连续的存储单元依次存储线性表的数据元素,称为线性表的顺序存储结构。它以物理位置相邻来表示线性表中数据元素间的逻辑关系,可随机存取表中任一元素。顺序表示的又叫顺序表,也就是用数组来实现的列表。任意的存储单元存储线性表中的数据元素,称为线性表的链式存储结构。它的存储单元可以是连续的,也可以是不连续的。在表示数据元素之间的逻辑关系时,除了存储其本身的信息之外,还需存储一个指示其直接后继的信息,也就是用链表来实现的列表。队列 (queue)和先进后出的栈(stack)。接下来我们会来实现链表形式的双端列表,也叫双端队列,这个数据结构应用场景更广泛一点。在实际工程应用上,缓存数据库Redis的列表List基本类型就是用它来实现的。二、实现双端列表
// 双端列表,双端队列
type DoubleList struct {
head *ListNode // 指向链表头部
tail *ListNode // 指向链表尾部
len int // 列表长度
lock sync.Mutex // 为了进行并发安全pop操作
}
// 列表节点
type ListNode struct {
pre *ListNode // 前驱节点
next *ListNode // 后驱节点
value string // 值
}
DoubleList指向队列头部head和尾部tail的指针字段,方便找到链表最前和最后的节点,并且链表节点之间是双向链接的,链表的第一个元素的前驱节点为nil,最后一个元素的后驱节点也为nil。如图: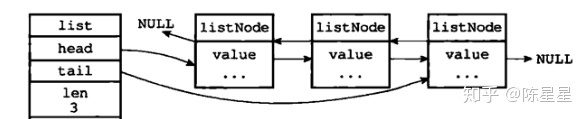
Golang标准库container/list中实现的不一样,感兴趣的可以阅读标准库的实现。2.1.列表节点普通操作
// 获取节点值
func (node *ListNode) GetValue() string {
return node.value
}
// 获取节点前驱节点
func (node *ListNode) GetPre() *ListNode {
return node.pre
}
// 获取节点后驱节点
func (node *ListNode) GetNext() *ListNode {
return node.next
}
// 是否存在后驱节点
func (node *ListNode) HashNext() bool {
return node.pre != nil
}
// 是否存在前驱节点
func (node *ListNode) HashPre() bool {
return node.next != nil
}
// 是否为空节点
func (node *ListNode) IsNil() bool {
return node == nil
}
ListNode的操作,主要判断节点是否为空,有没有后驱和前驱节点,返回值等,时间复杂度都是O(1)。2.2.从头部开始某个位置前插入新节点
// 添加节点到链表头部的第N个元素之前,N=0表示新节点成为新的头部
func (list *DoubleList) AddNodeFromHead(n int, v string) {
// 加并发锁
list.lock.Lock()
defer list.lock.Unlock()
// 索引超过列表长度,一定找不到,panic
if n > list.len {
panic("index out")
}
// 先找出头部
node := list.head
// 往后遍历拿到第 N+1 个位置的元素
for i := 1; i // 索引超过列表长度,一定找不到,panic
if n > list.len {
panic("index out")
}
n=0表示新节点想成为新的链表头部,n=1表示插入到链表头部数起第二个节点之前,新节点成为第二个节点,以此类推。node := list.head,然后往后面遍历,定位到索引指定的节点node:// 往后遍历拿到第 N+1 个位置的元素
for i := 1; i newNode := new(ListNode)。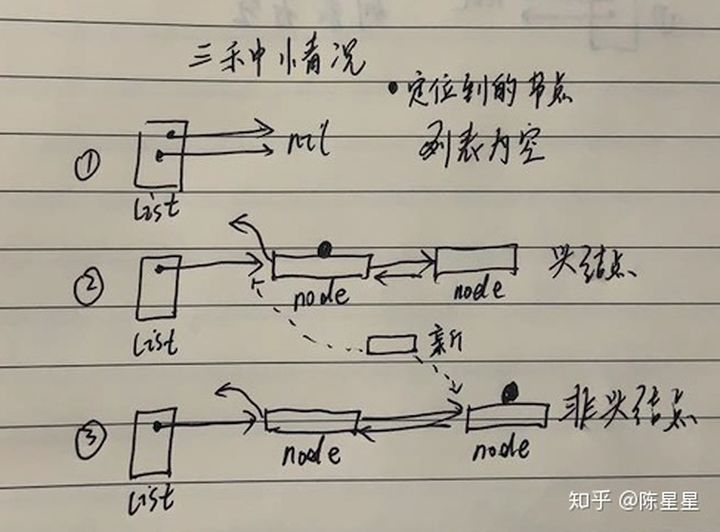
node是否为空,如果为空,表明列表没有元素,将新节点设置为新头部和新尾部。pre := node.pre。pre.IsNil(),表明定位到的节点node为头部,那么新节点要取代它,成为新的头部:if pre.IsNil() {
// 将新节点链接在老头部之前
newNode.next = node
node.pre = newNode
// 新节点成为头部
list.head = newNode
}
newNode.next = node,老头部的前驱为新头部:node.pre = newNode,并且新头部变化:list.head = newNode。node不是头部节点,那么我们只需将新节点链接到节点node之前即可:// 定位到的节点的前驱节点 pre 现在链接到新节点前
pre.next = newNode
newNode.pre = pre
// 定位到的节点链接到新节点之后
newNode.next = node
node.pre = newNode
pre.next = newNode,新节点的前驱设置为定位节点的前驱节点:newNode.pre = pre。newNode.next = node,定位到的节点的前驱设置为:node.pre = newNode。n=0,那么时间复杂度为O(1),否则为O(n)。2.3.从尾部开始某个位置后插入新节点
// 添加节点到链表尾部的第N个元素之后,N=0表示新节点成为新的尾部
func (list *DoubleList) AddNodeFromTail(n int, v string) {
// 加并发锁
list.lock.Lock()
defer list.lock.Unlock()
// 索引超过列表长度,一定找不到,panic
if n > list.len {
panic("index out")
}
// 先找出尾部
node := list.tail
// 往前遍历拿到第 N+1 个位置的元素
for i := 1; i 2.4.从头部开始某个位置获取列表节点
// 从头部开始往后找,获取第N+1个位置的节点,索引从0开始。
func (list *DoubleList) IndexFromHead(n int) *ListNode {
// 索引超过或等于列表长度,一定找不到,返回空指针
if n >= list.len {
return nil
}
// 获取头部节点
node := list.head
// 往后遍历拿到第 N+1 个位置的元素
for i := 1; i O(n)。2.5.从尾部开始某个位置获取列表节点
// 从尾部开始往前找,获取第N+1个位置的节点,索引从0开始。
func (list *DoubleList) IndexFromTail(n int) *ListNode {
// 索引超过或等于列表长度,一定找不到,返回空指针
if n >= list.len {
return nil
}
// 获取尾部节点
node := list.tail
// 往前遍历拿到第 N+1 个位置的元素
for i := 1; i 2.6.从头部开始移除并返回某个位置的节点
// 从头部开始往后找,获取第N+1个位置的节点,并移除返回
func (list *DoubleList) PopFromHead(n int) *ListNode {
// 加并发锁
list.lock.Lock()
defer list.lock.Unlock()
// 索引超过或等于列表长度,一定找不到,返回空指针
if n >= list.len {
return nil
}
// 获取头部
node := list.head
// 往后遍历拿到第 N+1 个位置的元素
for i := 1; i n >= list.len,如果超出直接返回空指针。N+1个位置的元素:node = node.next。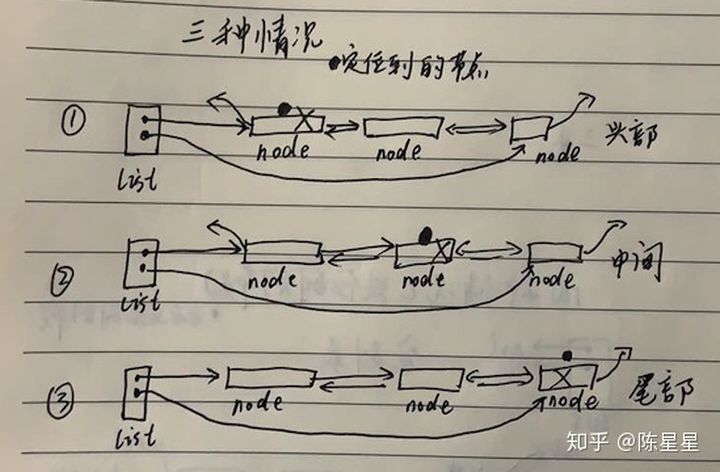
// 移除的节点的前驱和后驱
pre := node.pre
next := node.next
pre.IsNil() && next.IsNil(),那么要移除的节点是链表中唯一的节点,直接将列表头部和尾部置空即可。pre.IsNil(),表示移除的是头部节点,那么头部节点的下一个节点要成为新的头部:list.head = next,并且这时新的头部前驱要设置为空:next.pre = nil。next.IsNil(),表示移除的是尾部节点,需要将尾部节点的前一个节点设置为新的尾部:list.tail = pre,并且这时新的尾部后驱要设置为空:pre.next = nil。// 移除的是中间节点
pre.next = next
next.pre = pre
O(n)。2.7.从尾部开始移除并返回某个位置的节点
// 从尾部开始往前找,获取第N+1个位置的节点,并移除返回
func (list *DoubleList) PopFromTail(n int) *ListNode {
// 加并发锁
list.lock.Lock()
defer list.lock.Unlock()
// 索引超过或等于列表长度,一定找不到,返回空指针
if n >= list.len {
return nil
}
// 获取尾部
node := list.tail
// 往前遍历拿到第 N+1 个位置的元素
for i := 1; i 2.8.完整例子
package main
import (
"fmt"
"sync"
)
// 双端列表,双端队列
type DoubleList struct {
head *ListNode // 指向链表头部
tail *ListNode // 指向链表尾部
len int // 列表长度
lock sync.Mutex // 为了进行并发安全pop操作
}
// 列表节点
type ListNode struct {
pre *ListNode // 前驱节点
next *ListNode // 后驱节点
value string // 值
}
// 获取节点值
func (node *ListNode) GetValue() string {
return node.value
}
// 获取节点前驱节点
func (node *ListNode) GetPre() *ListNode {
return node.pre
}
// 获取节点后驱节点
func (node *ListNode) GetNext() *ListNode {
return node.next
}
// 是否存在后驱节点
func (node *ListNode) HashNext() bool {
return node.pre != nil
}
// 是否存在前驱节点
func (node *ListNode) HashPre() bool {
return node.next != nil
}
// 是否为空节点
func (node *ListNode) IsNil() bool {
return node == nil
}
// 返回列表长度
func (list *DoubleList) Len() int {
return list.len
}
// 添加节点到链表头部的第N个元素之前,N=0表示新节点成为新的头部
func (list *DoubleList) AddNodeFromHead(n int, v string) {
// 加并发锁
list.lock.Lock()
defer list.lock.Unlock()
// 索引超过列表长度,一定找不到,panic
if n > list.len {
panic("index out")
}
// 先找出头部
node := list.head
// 往后遍历拿到第 N+1 个位置的元素
for i := 1; i list.len {
panic("index out")
}
// 先找出尾部
node := list.tail
// 往前遍历拿到第 N+1 个位置的元素
for i := 1; i = list.len {
return nil
}
// 获取头部节点
node := list.head
// 往后遍历拿到第 N+1 个位置的元素
for i := 1; i = list.len {
return nil
}
// 获取尾部节点
node := list.tail
// 往前遍历拿到第 N+1 个位置的元素
for i := 1; i = list.len {
return nil
}
// 获取头部
node := list.head
// 往后遍历拿到第 N+1 个位置的元素
for i := 1; i = list.len {
return nil
}
// 获取尾部
node := list.tail
// 往前遍历拿到第 N+1 个位置的元素
for i := 1; i you
love
I
may
happy
----------
you
love
I
may
happy
----------
you
love
I
may
happy
----------
len 0
系列文章入口
文章标题:数据结构和算法(Golang实现)(15)常见数据结构-列表
文章链接:http://soscw.com/index.php/essay/54998.html