线性时间排序

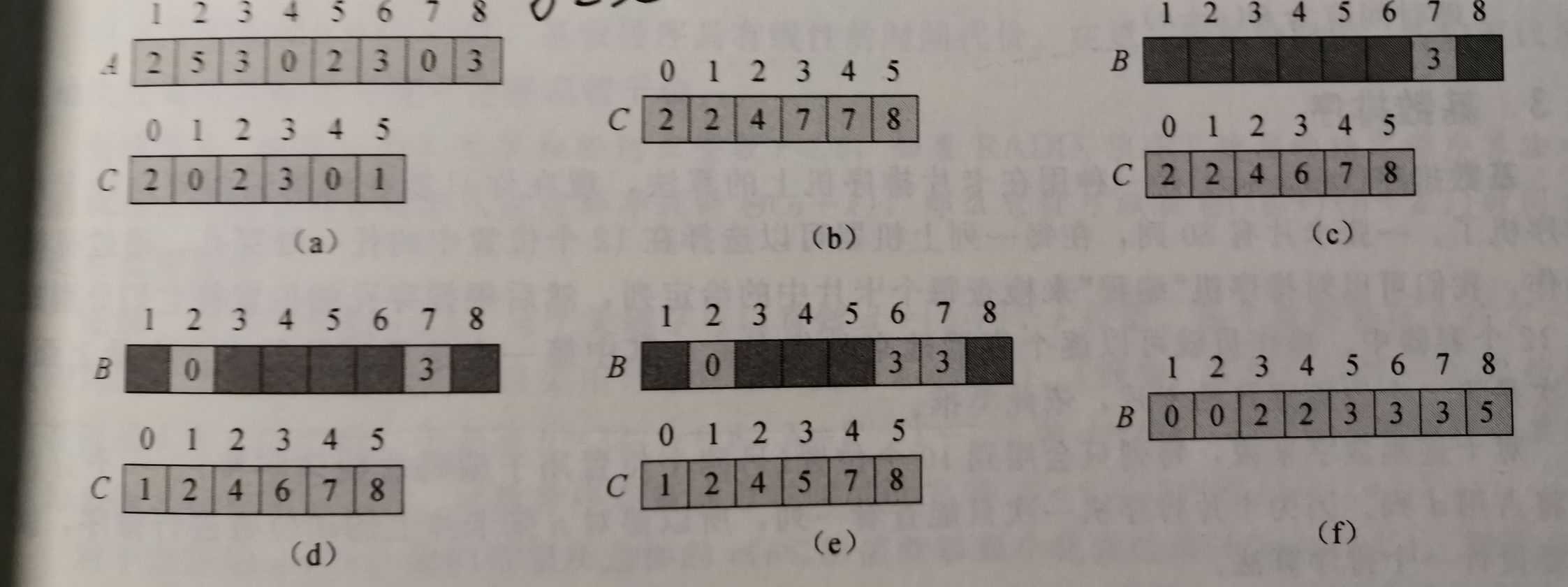
def Counting_Sort(A,B,k):
    for i in range(k+1):
        c[i]=0
    for j in range(1,len(A)):
        c[A[j]]=c[A[j]]+1
    for i in range(1,k+1):
        c[i]=c[i]+c[i-1]
    for j in range(len(A),0,-1):
        B[c[A[j]]]=A[j]
        c[A[j]]=c[A[j]]-1

#include 
#include using namespace std;
const n=10,m=4;
int Max(int B[n][m],int h)//O(n)
{//求最大k值
    int k=0;
    for (int i=0;i//O(n)
    {
        if (B[i][h]>k)
        {
           k=B[i][h];
        }
    }
    return k;
}
void COUNTING_SORT(int B[n][m],int C[n],int k,int h)//O(k)+O(n)+O(k)+O(n)=O(n+k)
{//计数排序
   
    int *D=new int[k+1];
    for (int i=0;i//O(k)
    {
        D[i]=0;
    }
    for (int j=0;j//O(n)
    {
        D[B[j][h]]=D[B[j][h]]+1;
    }
    for (i=0;i//O(k)
    {
        D[i+1]=D[i+1]+D[i];
    }
    for (j=n-1;j>=0;j--)//O(n)
    {
        C[D[B[j][h]]-1]=j;//把排好序的下标存放到数组C中以便按顺序把它存储到辅助数组E中。
        D[B[j][h]]=D[B[j][h]]-1;
    }
}
int Converted_to_Decimal(int A[],int B[][m],int i)//O(d)+O(d)=O(d)
{//此函数是将十进制数以2维数组B的形式存放。
    int x=A[i];
    for (int j=0;x>0;j++ )//O(d)循环了j    {
        B[i][j]=x%10;
        x=x/10;
    }
    if (jm)
    {
        for (int k=j;k//O(d) 循环了d-j次
        {
            B[i][k]=0;
        }
    }
    return j;
}
void Radix_sort(int A[n],int B[][m],int C[n],int E[n],int d)
{
    d=m;
    for ( int i=0;i//O(nd)
    {
        Converted_to_Decimal(A,B,i);
    }
    for ( i=0;i//O(d) d为位数
    {//因为d
        int k=Max(B,i);//O(n)
        COUNTING_SORT(B,C,k,i);//O(n+k)
        for (int i=0;i//O(n)
        {
            E[i]=A[C[i]];//每位上排好序后，将其复制到辅助数组E上。
        }
        for ( i=0;i//O(n)
        {
            Converted_to_Decimal(E,B,i);//把辅助数组E上的数转换成二维数组存放到二维数组B中。
        }
        for (i=0;i//O(n)
        {
            A[i]=E[i];//每次将按位排好序的数存放到数组A中以便在下一次循环中对下一位进行排序。
        }
    }//所以Radix_sort时间复杂度为O(d(n+k))
    //O(nd)+O(d(n+k))=O(d(n+k))
}
void main()
{
    srand( (unsigned)time( NULL ) );
    int A[n]={0};
    for (int i=0;i)
    {
        A[i]=rand()%(n);
    }
    int  B[n][m]={0},C[n]={0},E[n]={0};
    Radix_sort(A,B,C,E,m);
    for ( i=0;i)
    {
        cout" ";
    }
}

class bucketSort(object):
    def insertSort(self,a):
        n=len(a)
        if n:
            pass
        for i in range(1,n):
            key=a[i]
            j=i-1
            while keyand j>=0:
                a[j+1]=a[j]
                j-=1
            a[j+1]=key
    def sort(self,a):
        n=len(a)
        s=[[] for i in xrange(n)]
        for i in a:
            s[int(i*n)].append(i)
        for i in s:
            self.insertSort(i)
        return [i for j in s for i in j]
    def __call__(self,a):
        return self.sort(a)