素数判定Miller_Rabin 算法详解
2021-02-18 06:18
标签:代码 dom 乘法 详解 基础 string math 复杂度 根据 最简单直观简单的素数判定方法就是试除法。对于判断数n是否是素数,我们从2开始一直到sqrt(n)。如果找到一个因子则判断n不是素数,否则是素数。代码如下: 如果要找到成1~n的所有素数那么这个时间代价就变为O(n^2),很多时候是不可接受的。 但是这个算法的弊端在于,为了判断一个大数是否是素数必须从从头开始扫描,而且空间代价也受不了,故不能离散的判断。 若n是奇素数,a是任意正整数(1≤ a≤ n−1), 证明:由费马定理,可以排除大部分非素数的情况(满足费马定理是素数的必要条件),给出一个奇素数n,显然n-1为一个偶数,存在 证明过程如下: 由p为一个素数可以推出 所以根据二次探测定理,可以推断 对于一个大数n,判断n是不是素数的时候,可以先考虑a(n-1)≡ 1(mod n) 对于n-1,一定可以拆分成2s+d: 可以从x = ad开始,依次平方s次,每次平方的时候模上n,按照之前的平方根定理,如果模上n的结果为1的话,那么x一定是1,或者是n-1,如果不满足则不是素数,x=x2,再次循环。 每次随机选一个在2-n-1的数字作为a,可以重复测试。 由于mod上的是n,n是一个大数,所以快速幂中的乘法,需要用快速加法来实现。不然就算模上之后再相乘也会溢出。 部分参考:https://www.cnblogs.com/fzl194/p/9046117.html 素数判定Miller_Rabin 算法详解 标签:代码 dom 乘法 详解 基础 string math 复杂度 根据 原文地址:https://www.cnblogs.com/jaszzz/p/12693251.htmlbool isPrime( long long n )
{
for(long long i = 2; i*i
所以随着学习的深入,我们了解到了素数筛法,即从2开始,2的倍数肯定不是素数,再向右扫描,如果扫描到素数,则重复之前的过程,剔除之后的部分合数(准确的说是关于当前质数的倍数),如果扫描到合数则跳过(表示前面已经更新过这个数不是素数)。然后都扫描一遍即可把1~n的素数求解出来。这个算法的复杂度略高于O(n)。素数筛代码如下:bool isprime[MAXN];
int prime[MAXN];
int cnt = 0;//保存素数个数
void getPrime()
{
for(int i = 1; i
Miller_rabin算法
算法的理论基础:
1. Fermat定理:
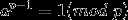
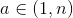 ,显然
,显然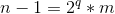 (q,m为任意整数)是成立的,所以
(q,m为任意整数)是成立的,所以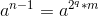 ,显然
,显然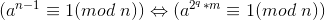 .
.2. 二次探测定理:
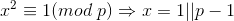
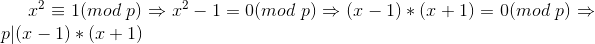
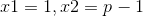 。
。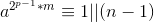 ,
,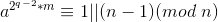 ……,
……,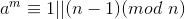 .
.3. 综上:
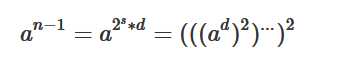
代码:
#include
上一篇:父类数组如何向下转型
下一篇:推荐算法-协同过滤推荐算法
文章标题:素数判定Miller_Rabin 算法详解
文章链接:http://soscw.com/index.php/essay/56918.html