回溯算法学习
2021-02-19 03:18
标签:决策 遍历 数字 排列 循环 return nbsp 组合 ref 解决一个回溯问题,实际上就是一个决策树的遍历过程。思考 3 个问题: 1、路径:也就是已经做出的选择。 2、选择列表:也就是你当前可以做的选择。 3、结束条件:也就是到达决策树底层,无法再做选择的条件。 回溯算法的框架: 其核心就是 for 循环里面的递归,在递归调用之前「做选择」,在递归调用之后「撤销选择」,特别简单。 排列组合, PS:为了简单清晰起见,全排列问题不包含重复数字。一般是这样: 先固定第一位为 1,然后第二位可以是 2,那么第三位只能是 3;然后可以把第二位变成 3,第三位就只能是 2 了;然后就只能变化第一位,变成 2,然后再穷举后两位…… 其实这就是回溯算法。 python代码如下,根据框架而写: 结果如下。 回溯算法学习 标签:决策 遍历 数字 排列 循环 return nbsp 组合 ref 原文地址:https://www.cnblogs.com/ljy1227476113/p/12687095.htmlresult = []
def backtrack(路径, 选择列表):
if 满足结束条件:
result.add(路径)
return
for 选择 in 选择列表:
做选择
backtrack(路径, 选择列表)
撤销选择
全排列问题
n 个不重复的数全排列共有 n! 个。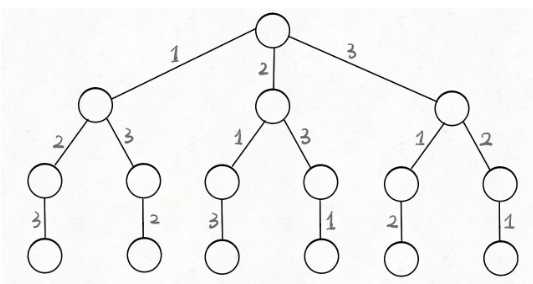
1 nums=[1,2,3]
2 result=[]
3 def backtrack(path,choices):
4 if len(path)==len(choices):
5 result.append(list(path))
6 return
7 for choice in choices:
8 if choice in path:continue
9 path.append(choice)
10 backtrack(path,choices)
11 path.pop(-1)
12
13 backtrack([],nums)
14 print(result)
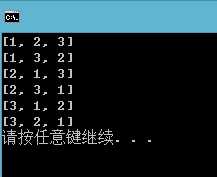
上一篇:python 三元表达式的