机器学习进度06（朴素贝叶斯算法、决策树、随机森林）

2021-03-06 05:27

阅读：472

标签：param max etc 数据集 log res 节点 otp 获取

朴素贝叶斯算法

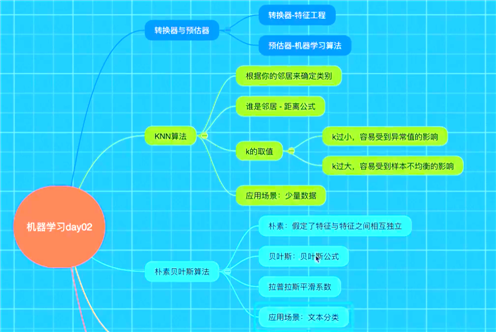
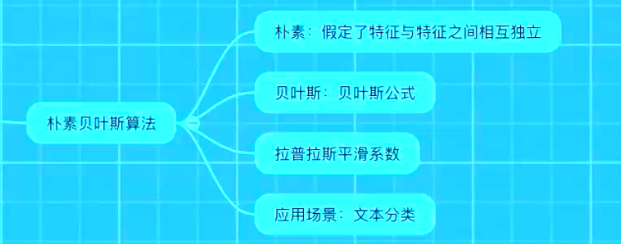
什么是朴素贝叶斯分类方法

技术图片

条件概率与联合概率

联合概率：包含多个条件，且所有条件同时成立的概率
- 记作：P(A,B)
- 特性：P(A, B) = P(A)P(B)
条件概率：就是事件A在另外一个事件B已经发生条件下的发生概率
- 记作：P(A|B)
- 特性：P(A1,A2|B) = P(A1|B)P(A2|B)

注意：此条件概率的成立，是由于A1,A2相互独立的结果(记忆)

技术图片

API

sklearn.naive_bayes.MultinomialNB(alpha = 1.0)
朴素贝叶斯分类
alpha：拉普拉斯平滑系数

技术图片

案例：20类新闻分类

技术图片

代码：

#案例：20类新闻分类

def nb_news():
    """
    用朴素贝叶斯算法对新闻进行分类
    :return:
    """
    # 1）获取数据
    news = fetch_20newsgroups(subset="all")

    # 2）划分数据集
    x_train, x_test, y_train, y_test = train_test_split(news.data, news.target)

    # 3）特征工程：文本特征抽取-tfidf
    transfer = TfidfVectorizer()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)

    # 4）朴素贝叶斯算法预估器流程
    estimator = MultinomialNB()
    estimator.fit(x_train, y_train)

    # 5）模型评估
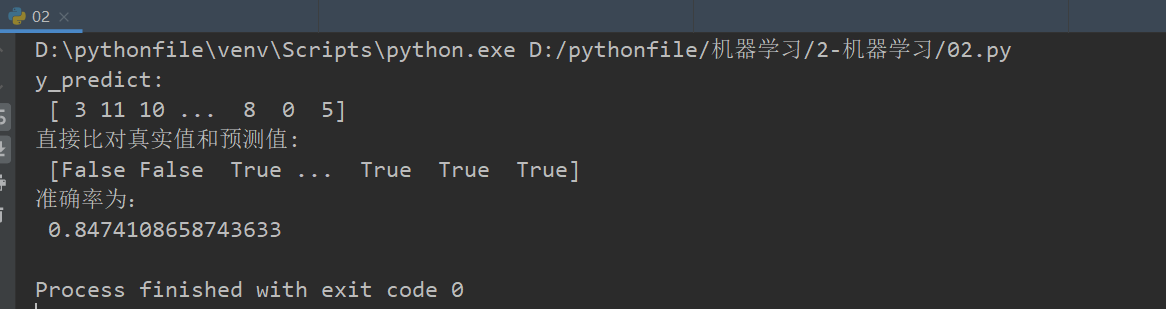
    # 方法1：直接比对真实值和预测值
    y_predict = estimator.predict(x_test)
    print("y_predict:\n", y_predict)
    print("直接比对真实值和预测值:\n", y_test == y_predict)

    # 方法2：计算准确率
    score = estimator.score(x_test, y_test)
    print("准确率为：\n", score)

    return None

if __name__=="__main__":
    nb_news()

技术图片

总结

优点：
- 朴素贝叶斯模型发源于古典数学理论，有稳定的分类效率。
- 对缺失数据不太敏感，算法也比较简单，常用于文本分类。
- 分类准确度高，速度快
缺点：
- 由于使用了样本属性独立性的假设，所以如果特征属性有关联时其效果不好

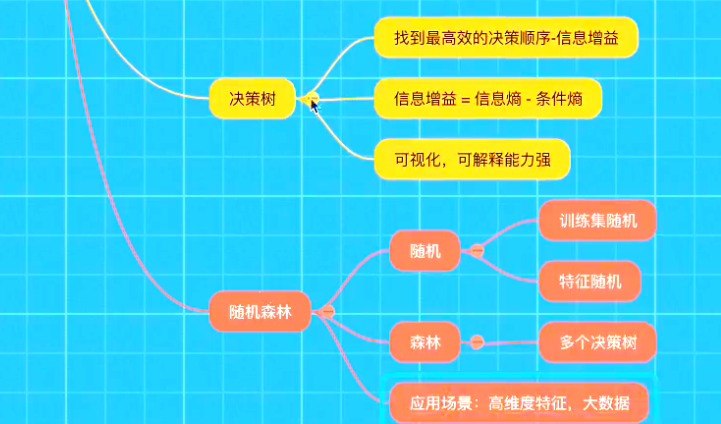
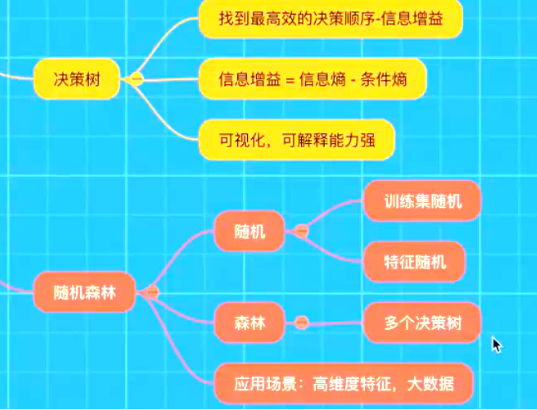
决策树

认识决策树

决策树思想的来源非常朴素，程序设计中的条件分支结构就是if-then结构，最早的决策树就是利用这类结构分割数据的一种分类学习方法

技术图片

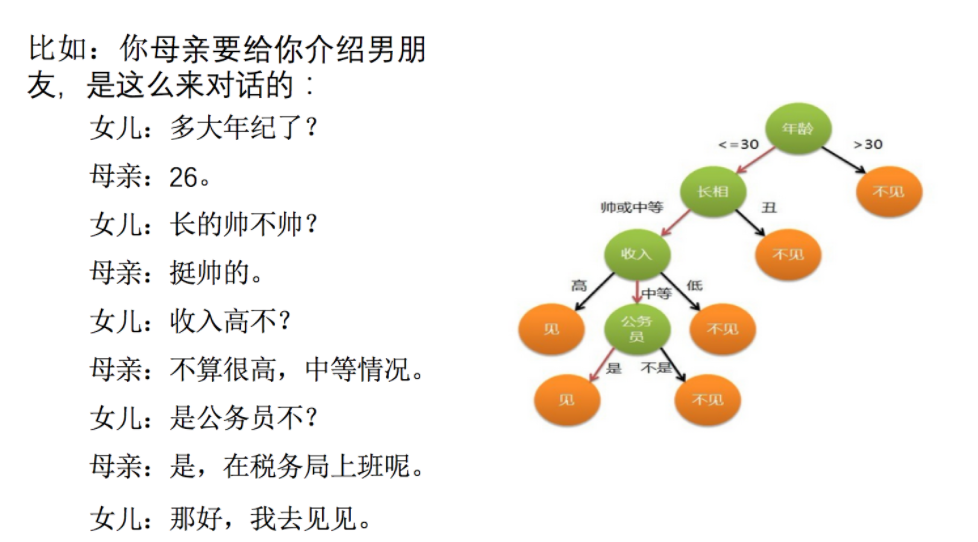
决策树分类原理详解

技术图片

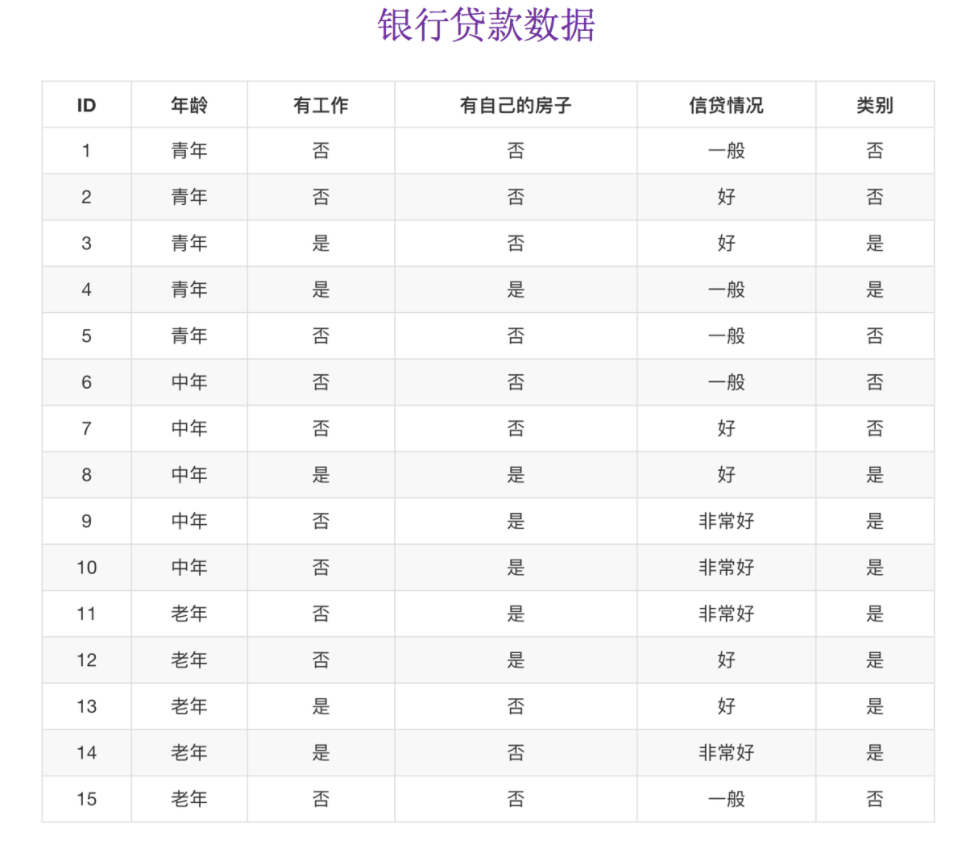
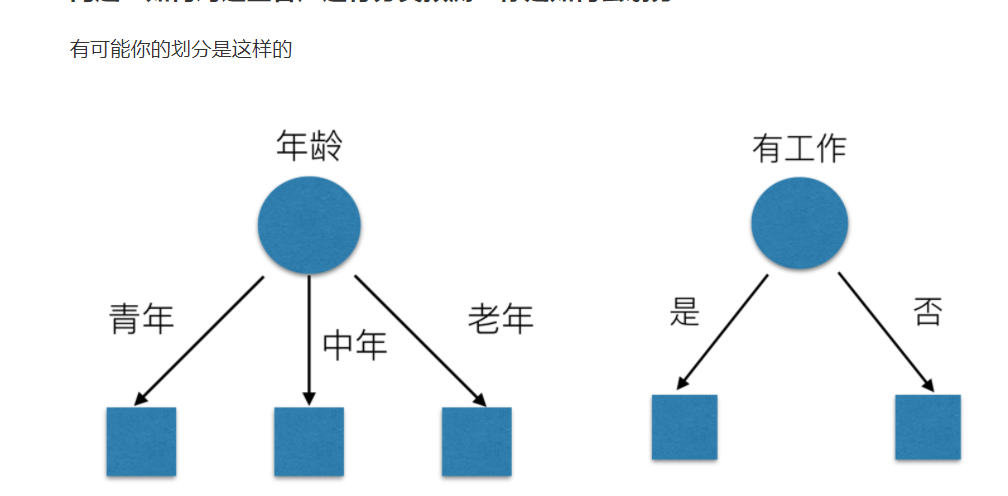
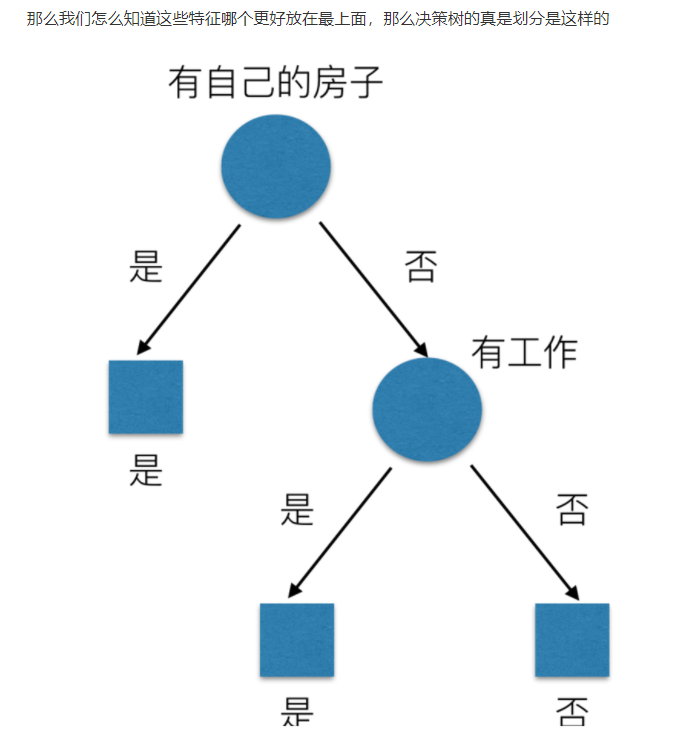
信息熵的定义

H的专业术语称之为信息熵，单位为比特。

总结（重要）
- 信息和消除不确定性是相联系的
当我们得到的额外信息（球队历史比赛情况等等）越多的话，那么我们猜测的代价越小（猜测的不确定性减小）

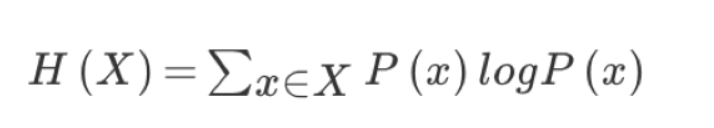
决策树的划分依据之一------信息增益

定义与公式

特征A对训练数据集D的信息增益g(D,A),定义为集合D的信息熵H(D)与特征A给定条件下D的信息条件熵H(D|A)之差，即公式为：

技术图片

决策树的三种算法实现

当然决策树的原理不止信息增益这一种，还有其他方法。但是原理都类似，我们就不去举例计算。

ID3
- 信息增益最大的准则
C4.5
- 信息增益比最大的准则
CART
- 分类树: 基尼系数最小的准则在sklearn中可以选择划分的默认原则
- 优势：划分更加细致（从后面例子的树显示来理解）

决策树API

class sklearn.tree.DecisionTreeClassifier(criterion=’gini’, max_depth=None,random_state=None)
决策树分类器
criterion:默认是’gini’系数，也可以选择信息增益的熵’entropy’
max_depth:树的深度大小
random_state:随机数种子
其中会有些超参数：max_depth:树的深度大小

其它超参数我们会结合随机森林讲解

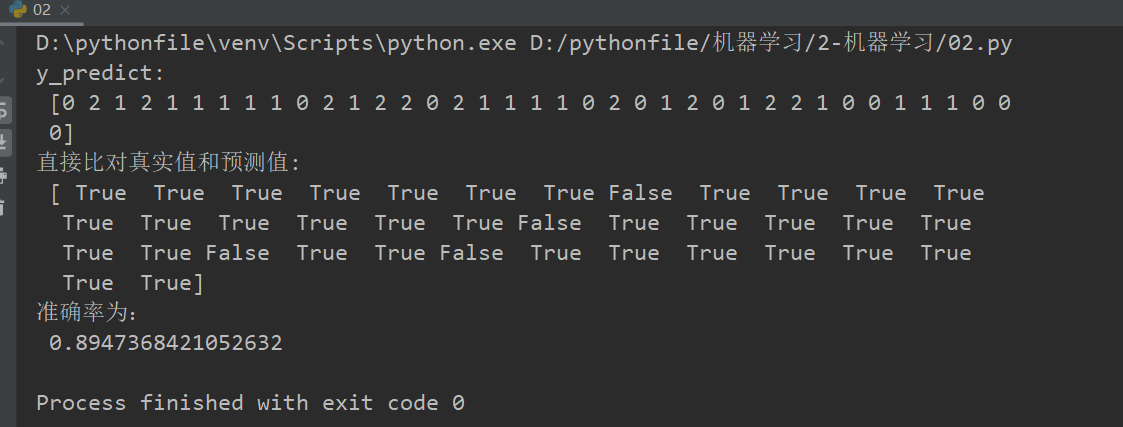
案例：用决策树对鸢尾花进行分类

#用决策树对鸢尾花进行分类
def decision_iris():
    """
    用决策树对鸢尾花进行分类
    :return:
    """
    # 1）获取数据集
    iris = load_iris()

    # 2）划分数据集
    x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=22)

    # 3）决策树预估器
    estimator = DecisionTreeClassifier(criterion="entropy")
    estimator.fit(x_train, y_train)

    # 4）模型评估
    # 方法1：直接比对真实值和预测值
    y_predict = estimator.predict(x_test)
    print("y_predict:\n", y_predict)
    print("直接比对真实值和预测值:\n", y_test == y_predict)

    # 方法2：计算准确率
    score = estimator.score(x_test, y_test)
    print("准确率为：\n", score)

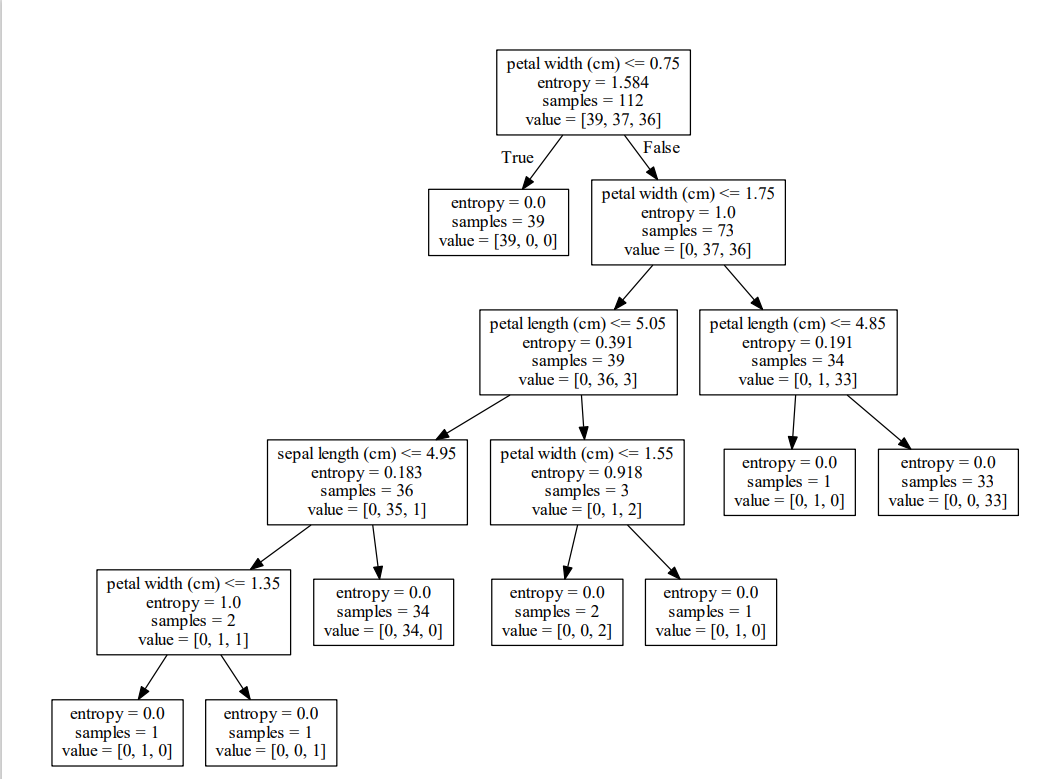
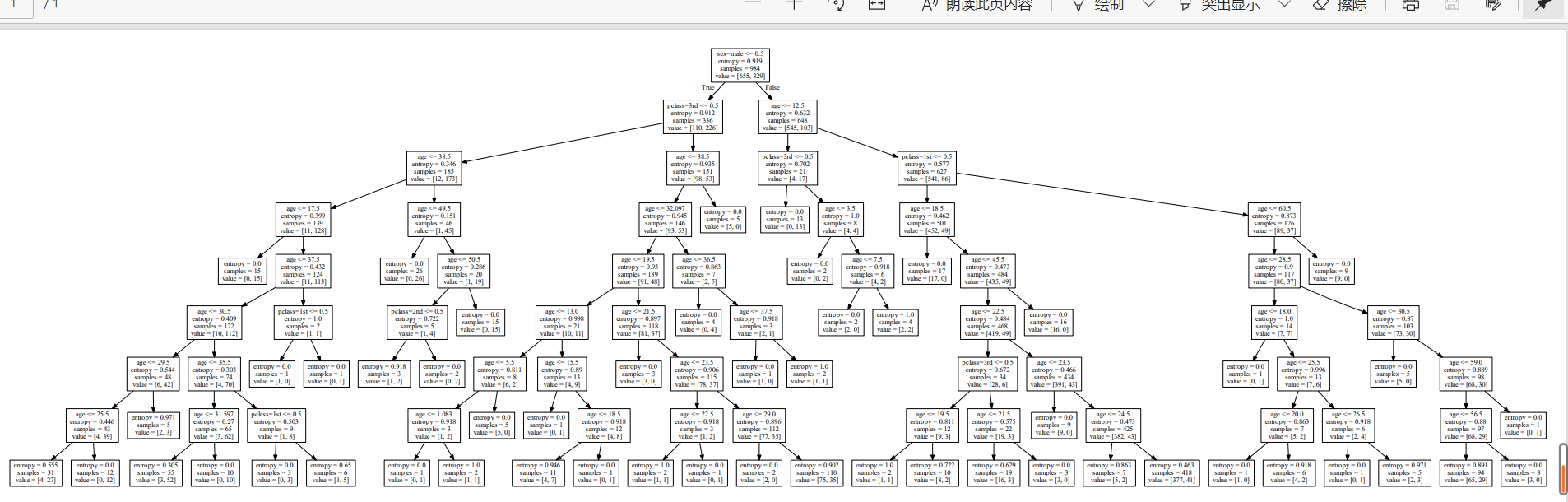
　　# 可视化决策树
　　#export_graphviz(estimator, out_file="iris_tree.dot", feature_names=iris.feature_names)
　　dot_data = export_graphviz(estimator, out_file=None, feature_names=iris.feature_names)
　　graph = pydotplus.graph_from_dot_data(dot_data)
　　graph.write_pdf("iris.pdf")

return None if __name__=="__main__": decision_iris()

技术图片

保存树的结构到dot文件

1、sklearn.tree.export_graphviz() 该函数能够导出DOT格式
tree.export_graphviz(estimator,out_file=‘tree.dot’,feature_names=[‘’,’’])
2、工具:(能够将dot文件转换为pdf、png)
安装graphviz
ubuntu:sudo apt-get install graphviz Mac:brew install graphviz
3、运行命令
然后我们运行这个命令
dot -Tpng tree.dot -o tree.png

技术图片

上边写过代码：

技术图片

总结

优点：
- 朴素贝叶斯模型发源于古典数学理论，有稳定的分类效率。
- 对缺失数据不太敏感，算法也比较简单，常用于文本分类。
- 分类准确度高，速度快
缺点：
- 由于使用了样本属性独立性的假设，所以如果特征属性有关联时其效果不好

案例：泰坦尼克号乘客生存预测

数据来源和说明：https://www.kaggle.com/zephyrzhan522/titanic-prediction-dl-vs-ml

技术图片

分析

选择我们认为重要的几个特征 [‘pclass‘, ‘age‘, ‘sex‘]
填充缺失值
特征中出现类别符号，需要进行one-hot编码处理(DictVectorizer)
- x.to_dict(orient="records") 需要将数组特征转换成字典数据
数据集划分
决策树分类预测

代码

#泰坦尼克号乘客生存预测
def titanic():
    # 1、获取数据
    path = "titanic.txt"
    titanic = pd.read_csv(path)
    # 筛选特征值和目标值
    x = titanic[["pclass", "age", "sex"]]
    y = titanic["survived"]
    # 2、数据处理
    # 1）缺失值处理
    x["age"].fillna(x["age"].mean(), inplace=True) #填充平均值
    # 2) 转换成字典
    x = x.to_dict(orient="records")
    # 3、数据集划分
    x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=22)
    # 4、字典特征抽取
    transfer = DictVectorizer()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)
    # 3）决策树预估器
    estimator = DecisionTreeClassifier(criterion="entropy", max_depth=8)
    estimator.fit(x_train, y_train)

    # 4）模型评估
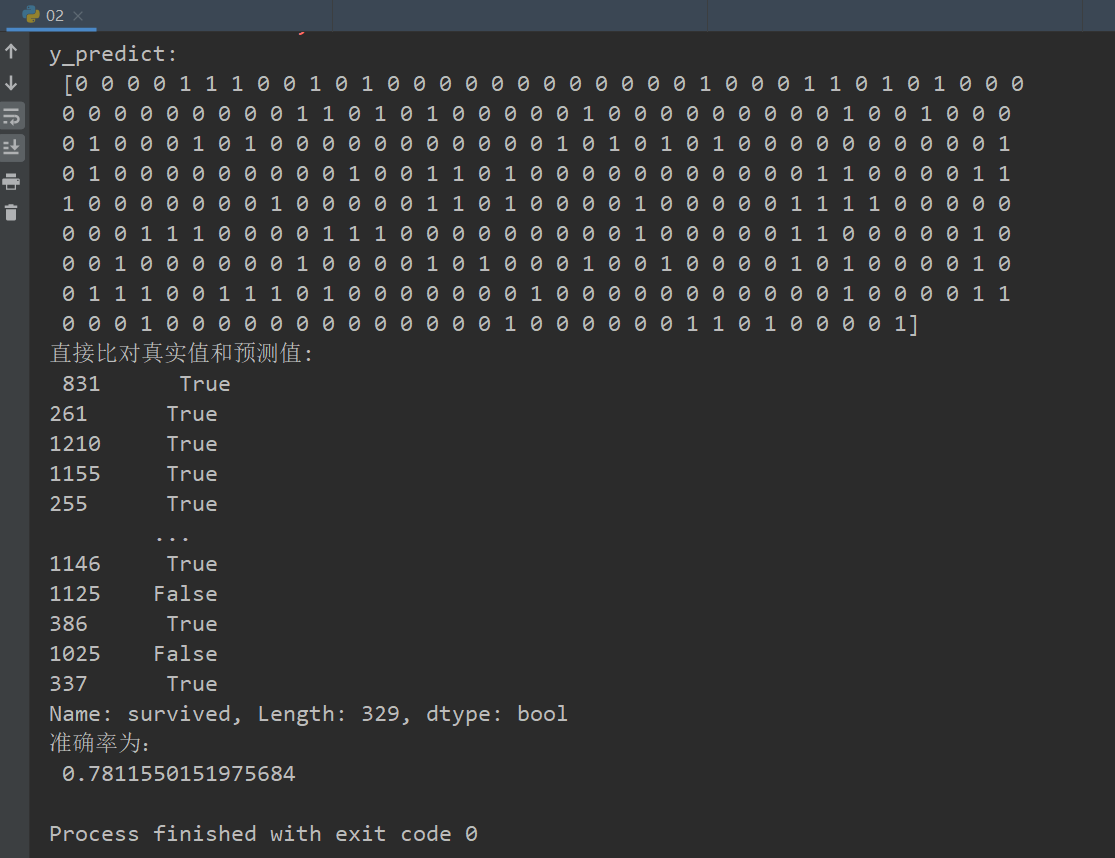
    # 方法1：直接比对真实值和预测值
    y_predict = estimator.predict(x_test)
    print("y_predict:\n", y_predict)
    print("直接比对真实值和预测值:\n", y_test == y_predict)

    # 方法2：计算准确率
    score = estimator.score(x_test, y_test)
    print("准确率为：\n", score)

    # 可视化决策树
    dot_data =export_graphviz(estimator, out_file=None, feature_names=transfer.get_feature_names())
    graph = pydotplus.graph_from_dot_data(dot_data)
    graph.write_pdf("titanic.pdf")

if __name__=="__main__":
    titanic()

技术图片

随机森林

什么是集成学习方法

集成学习通过建立几个模型组合的来解决单一预测问题。它的工作原理是生成多个分类器/模型，各自独立地学习和作出预测。这些预测最后结合成组合预测，因此优于任何一个单分类的做出预测。

什么是随机森林

在机器学习中，随机森林是一个包含多个决策树的分类器，并且其输出的类别是由个别树输出的类别的众数而定。

例如, 如果你训练了5个树, 其中有4个树的结果是True, 1个数的结果是False, 那么最终投票结果就是True。

随机森林原理过程

学习算法根据下列算法而建造每棵树：

用N来表示训练用例（样本）的个数，M表示特征数目。
- 1、一次随机选出一个样本，重复N次，（有可能出现重复的样本）
- 2、随机去选出m个特征, m
采取bootstrap抽样

为什么采用BootStrap抽样

为什么要随机抽样训练集？　　
- 如果不进行随机抽样，每棵树的训练集都一样，那么最终训练出的树分类结果也是完全一样的
为什么要有放回地抽样？
- 如果不是有放回的抽样，那么每棵树的训练样本都是不同的，都是没有交集的，这样每棵树都是“有偏的”，都是绝对“片面的”（当然这样说可能不对），也就是说每棵树训练出来都是有很大的差异的；而随机森林最后分类取决于多棵树（弱分类器）的投票表决。

API

class sklearn.ensemble.RandomForestClassifier(n_estimators=10, criterion=’gini’, max_depth=None, bootstrap=True, random_state=None, min_samples_split=2)

随机森林分类器
n_estimators：integer，optional（default = 10）森林里的树木数量120,200,300,500,800,1200
criteria：string，可选（default =“gini”）分割特征的测量方法
max_depth：integer或None，可选（默认=无）树的最大深度 5,8,15,25,30
max_features="auto”,每个决策树的最大特征数量
If "auto", then max_features=sqrt(n_features).
If "sqrt", then max_features=sqrt(n_features) (same as "auto").
If "log2", then max_features=log2(n_features).
If None, then max_features=n_features.
bootstrap：boolean，optional（default = True）是否在构建树时使用放回抽样
min_samples_split:节点划分最少样本数
min_samples_leaf:叶子节点的最小样本数
超参数：n_estimator, max_depth, min_samples_split,min_samples_leaf

代码：

#泰坦尼克号乘客生存预测随机森林
def suijisanli_demo():
    # 1、获取数据
    path = "titanic.csv"
    titanic = pd.read_csv(path)
    # 筛选特征值和目标值
    x = titanic[["pclass", "age", "sex"]]
    y = titanic["survived"]
    # 2、数据处理
    # 1）缺失值处理
    x["age"].fillna(x["age"].mean(), inplace=True)
    # 2) 转换成字典
    x = x.to_dict(orient="records")
    # 3、数据集划分
    x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=22)
    # 4、字典特征抽取
    transfer = DictVectorizer()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)

    #随机森林预估器
    estimator = RandomForestClassifier()
    # 加入网格搜索与交叉验证
    # 参数准备
    param_dict = {"n_estimators": [120, 200, 300, 500, 800, 1200], "max_depth": [5, 8, 15, 25, 30]}
    estimator = GridSearchCV(estimator, param_grid=param_dict, cv=3)
    estimator.fit(x_train, y_train)

    # 5）模型评估
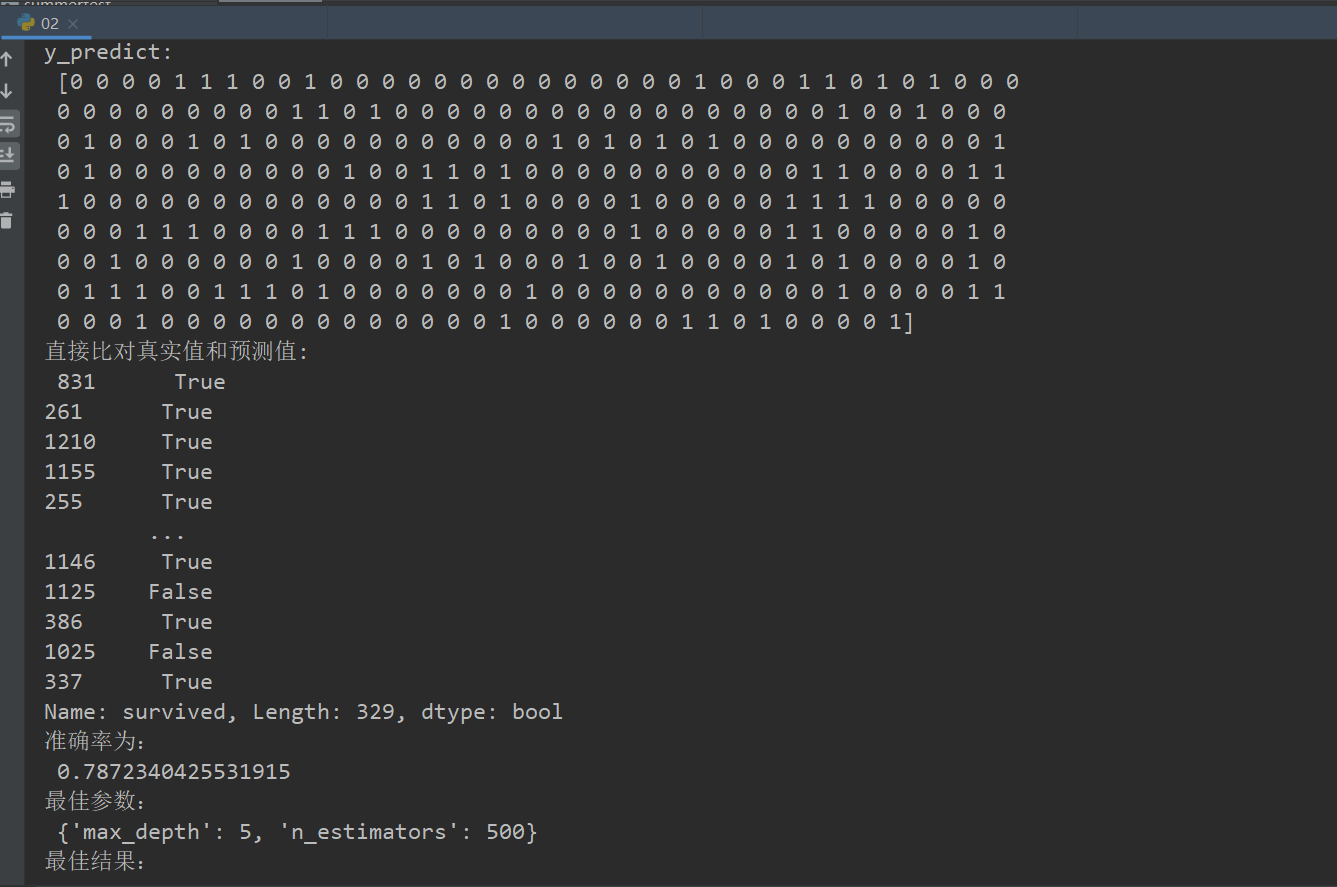
    # 方法1：直接比对真实值和预测值
    y_predict = estimator.predict(x_test)
    print("y_predict:\n", y_predict)
    print("直接比对真实值和预测值:\n", y_test == y_predict)

    # 方法2：计算准确率
    score = estimator.score(x_test, y_test)
    print("准确率为：\n", score)

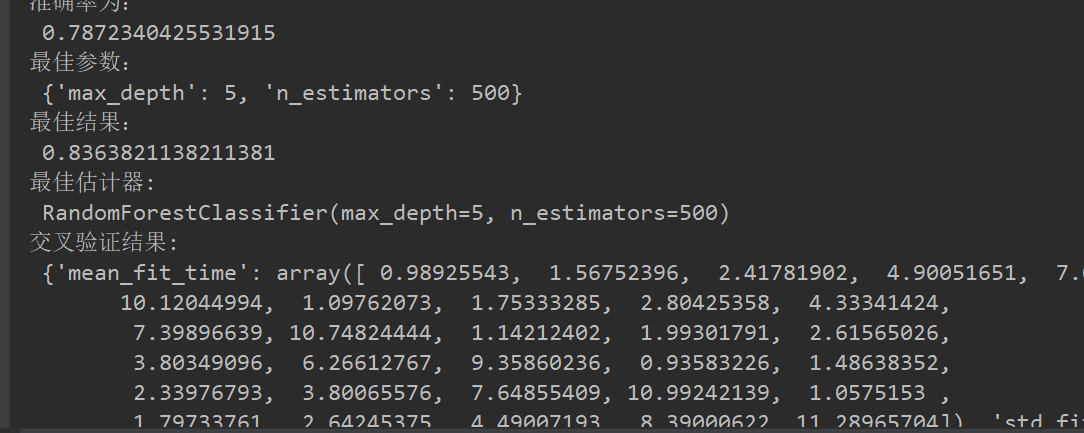
    # 最佳参数：best_params_
    print("最佳参数：\n", estimator.best_params_)
    # 最佳结果：best_score_
    print("最佳结果：\n", estimator.best_score_)
    # 最佳估计器：best_estimator_
    print("最佳估计器:\n", estimator.best_estimator_)
    # 交叉验证结果：cv_results_
    print("交叉验证结果:\n", estimator.cv_results_)
if __name__=="__main__":
    suijisanli_demo()