标签:pos init targe 图片 define ret const return mina
目录
- 2020 Petrozavodsk Winter Camp, Jagiellonian U Contest
- B. Binomial
- E. Contamination
- G. Invited Speakers
- H. Lighthouses
- I. Sum of Palindromes
- J. Space Gophers
- L. Wizards Unite
2020 Petrozavodsk Winter Camp, Jagiellonian U Contest
B. Binomial
题意:给定一个数组 \(a_n\) ,求有几对数字 \((a_i,a_j)\) 满足 \(C^{a_i}_{a_j}\) 为奇数。
分析:\(C^m_n\) 为奇数的条件是 n & m = m ,这就转化成一个经典问题,参考博客:https://codeforces.com/blog/entry/45223
#include
using namespace std;
typedef long long LL;
const int maxn = 1e6 + 5;
int p[maxn];
LL a[1
E. Contamination
#include
using namespace std;
const int maxn = 4e6 + 5;
struct Node {
int type;
int h;
int p;
int y_max;
int x_min;
int x_max;
} node[maxn];
typedef pair pii;
pii c[maxn];
namespace Segment {
const int inf = -(2e9) - 100;
int tree[maxn > 1;
build(root > 1;
if (x = stdl && right > 1;
int res = inf;
if (stdl mid)
res = max(res, query(root q_x)
swap(p_x, q_x);
node[k].x_min = p_x;
node[k].x_max = q_x;
node[k].h = y_min;
node[k].y_max = y_max;
}
int cnt = 0;
for (int i = 1; i > 1].x_max = rh;
else
node[c[j].second >> 1].x_min = rh;
}
}
}
sort(node + 1, node + 1 + k, [&](const Node& a, const Node& b) {
if (a.h == b.h)
return a.type
G. Invited Speakers
题意:给定平面上两个大小为 \(n\) 的点集,要求给出一种构造方案,使得这两个点集中的点两两匹配(两个点之间画出一条折线段将它们连接称为匹配),并且不存在任意两对折线段有交点。(给定的点集不存在三点共线,不存在任意两点的横坐标或纵坐标相同)
分析:如下图,先将点集按照水平序排序,然后画矩形绕圈。
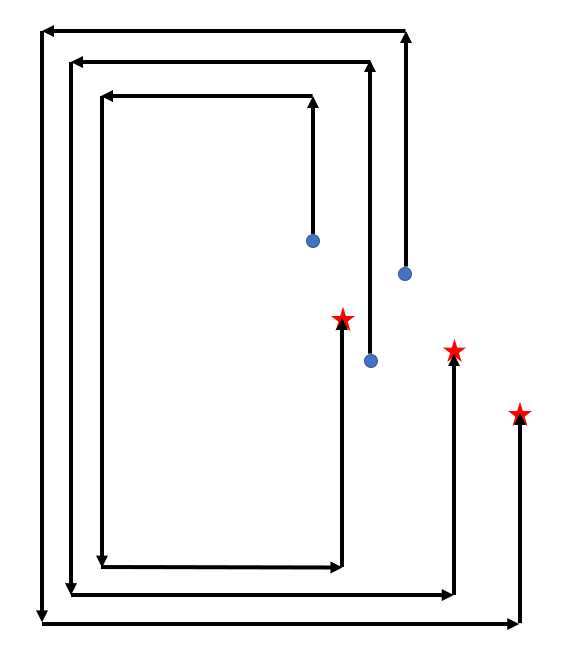
#include
using namespace std;
const int add = 500;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr); cout.tie(nullptr);
int t; cin >> t;
while (t--) {
int n; cin >> n;
vector > spot(n), table(n);
for (auto& i : spot) cin >> i.first >> i.second;
for (auto& i : table) cin >> i.first >> i.second;
sort(spot.begin(), spot.end());
sort(table.begin(), table.end());
for (int i = 0; i
H. Lighthouses
#include
using namespace std;
const int maxn = 305 * 2;
bool a[maxn][maxn];
long long x[maxn], y[maxn];
double dist(int a, int b) {
return sqrt((x[a] - x[b]) * (x[a] - x[b]) + (y[a] - y[b]) * (y[a] - y[b]));
}
double pre[maxn][maxn], suf[maxn][maxn];
int main() {
int t;
scanf("%d", &t);
while (t--) {
int n;
scanf("%d", &n);
for (int i = 1; i
I. Sum of Palindromes
题意:将一个大数拆成最多 \(25\) 个回文数。
分析:我们每次将问题规模折半,比如 \(123407897\) 就能够减去 \(123404321\) ;如果不能折半就找到一位退位,比如 \(123401234\) 可以减去 \(123393321\) (本来减去 \(123404321\) ,但是不行,因此退位)。
#include
using namespace std;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr); cout.tie(nullptr);
int t; cin >> t;
while (t--) {
string s; cin >> s;
vector a(s.length());
vector > ans;
for (int i = 0; i 1) ans.emplace_back(len - 1, 9);
ans.emplace_back(1, 1);
break;
}
}
vector tmp = a;
for (int i = 0; i > 1); ++i) tmp[i] = tmp[len - i - 1];
vector pa = a, pb = tmp;
reverse(pa.begin(), pa.end());
reverse(pb.begin(), pb.end());
if (pa > 1);
while (!tmp[pos]) tmp[pos++] = 9;
--tmp[pos];
for (int i = 0; i > 1); ++i) tmp[i] = tmp[len - i - 1];
}
ans.emplace_back(tmp);
for (int i = 0; i
J. Space Gophers
题意:在一个巨大的三维网格空间中建造 \(n\) 条垂直坐标系的隧道,\(q\) 个询问,询问两点之间是否可以通过隧道到达。
分析:考虑使用并查集维护,但是如何合并两条隧道较难处理,因为这个网格空间的量级是 \(1e6\) 的,我们不可能每次都将整条隧道中的点合并。假设建了一条 \((x,y,-1)\) 的隧道,如下图加粗蓝色柱体:
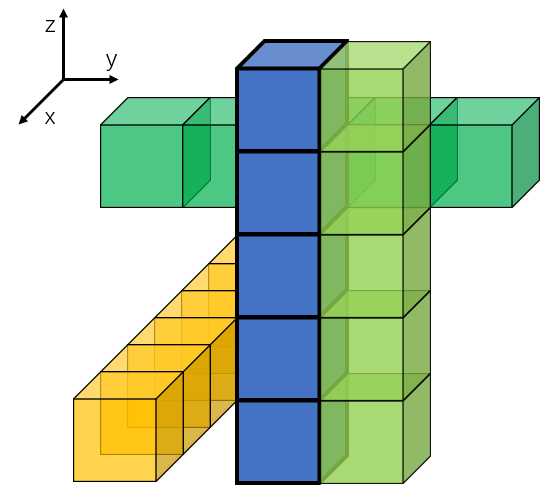
我们思考,如果建了这条 \((x,y,-1)\) 的隧道,有哪些隧道应该与之合并,显然 \(x,y,z\) 三个方向的隧道都应该被考虑到,如上图:
-
\(z\) 方向的四条相邻隧道(图中淡绿色透明隧道为这四条隧道之一)显然需要合并:\((x-1,y,-1),\ (x,y-1,-1),\ (x+1,y,-1),\ (x,y+1,-1)\) ;
-
\(y\) 方向上就比较麻烦(图中透明深绿色),因为只要满足 \(x‘\in \{x-1,x,x+1\}\) 的隧道 \((x‘,-1,z‘)\) 都应该与之合并;
-
\(x\) 方向上同理(图中透明黄色),只要满足 \(y‘\in \{y-1,y,y+1\}\) 的隧道 \((-1,y‘,z‘)\) 都应该与之合并。
实际上,我们发现对于这三个方向的隧道,我们可以分两类讨论:一类是需要合并的两个隧道方向一致的,如上方的情况 \(1\) ;另一类是需要合并的两个隧道方向不一致的,如上方的情况 \(2,3\) 。第一类情况很容易处理,我们直接用 \(std::map\) 存储三元集 \((x,y,-1)\) ,然后将 \((x-1,y,-1),\ (x,y-1,-1),\ (x+1,y,-1),\ (x,y+1,-1)\) 与其合并即可;第二类情况相对麻烦,我们考虑降维操作:将 \((x,y,-1)\) 的隧道分别投影到面 \(zOy,zOx\) ,然后分别用 \(y,x\) 坐标来指代这条隧道,然后我们就能够将 \(y‘\in\{y-1,y,y+1\},\ x‘\in\{x-1,x,x+1\}\) 的隧道合并了。
然后就写了个 TLE ,还要剪一下枝。。。
#define _CRT_SECURE_NO_WARNINGS
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")
#pragma GCC target("sse,sse2,sse3,ssse3,sse4,popcnt,abm,mmx,avx,tune=native")
#pragma comment(linker, "/stack:200000000")
#include
#define SIZE 1000010
using namespace std;
struct Triple {
int x, y, z;
Triple() {}
Triple(int x_, int y_, int z_) : x(x_), y(y_), z(z_) {}
bool operator > t;
while (t--) {
int n; cin >> n;
U.init(1000000);
vector > xy(SIZE), yz(SIZE), zx(SIZE), yx(SIZE), zy(SIZE), xz(SIZE);
map MP;
for (int i = 0; i > x >> y >> z;
if (x == -1) {
yz[y].insert(i);
zy[z].insert(i);
}
else if (y == -1) {
xz[x].insert(i);
zx[z].insert(i);
}
else {
xy[x].insert(i);
yx[y].insert(i);
}
MP[Triple(x, y, z)] = i;
}
for (auto it : MP) {
Triple tp = it.first;
int id = it.second;
if (tp.x == -1) {
for (auto y : { tp.y - 1, tp.y, tp.y + 1 }) {
for (auto i : yx[y]) {
U.union_vertices(i, id);
}
if (!yx[y].empty()) yx[y] = { *yx[y].begin() };
if (MP.count(Triple(-1, y, tp.z)))
U.union_vertices(MP[Triple(-1, y, tp.z)], id);
}
for (auto z : { tp.z - 1, tp.z, tp.z + 1 }) {
for (auto i : zx[z]) {
U.union_vertices(i, id);
}
if (!zx[z].empty()) zx[z] = { *zx[z].begin() };
if (MP.count(Triple(-1, tp.y, z)))
U.union_vertices(MP[Triple(-1, tp.y, z)], id);
}
}
else if (tp.y == -1) {
for (auto x : { tp.x - 1, tp.x, tp.x + 1 }) {
for (auto i : xy[x]) {
U.union_vertices(i, id);
}
if (!xy[x].empty()) xy[x] = { *xy[x].begin() };
if (MP.count(Triple(x, -1, tp.z)))
U.union_vertices(MP[Triple(x, -1, tp.z)], id);
}
for (auto z : { tp.z - 1, tp.z, tp.z + 1 }) {
for (auto i : zy[z]) {
U.union_vertices(i, id);
}
if (!zy[z].empty()) zy[z] = { *zy[z].begin() };
if (MP.count(Triple(tp.x, -1, z)))
U.union_vertices(MP[Triple(tp.x, -1, z)], id);
}
}
else {
for (auto x : { tp.x - 1, tp.x, tp.x + 1 }) {
for (auto i : xz[x]) {
U.union_vertices(i, id);
}
if (!xz[x].empty()) xz[x] = { *xz[x].begin() };
if (MP.count(Triple(x, tp.y, -1)))
U.union_vertices(MP[Triple(x, tp.y, -1)], id);
}
for (auto y : { tp.y - 1, tp.y, tp.y + 1 }) {
for (auto i : yz[y]) {
U.union_vertices(i, id);
}
if (!yz[y].empty()) yz[y] = { *yz[y].begin() };
if (MP.count(Triple(tp.x, y, -1)))
U.union_vertices(MP[Triple(tp.x, y, -1)], id);
}
}
}
auto getId = [&](Triple p) {
int x = p.x, y = p.y, z = p.z;
int id = -1;
if (MP.count(Triple(x, y, -1)))
id = MP[Triple(x, y, -1)];
if (MP.count(Triple(x, -1, z)))
id = MP[Triple(x, -1, z)];
if (MP.count(Triple(-1, y, z)))
id = MP[Triple(-1, y, z)];
return id;
};
int q; cin >> q;
while (q--) {
Triple a, b;
cin >> a.x >> a.y >> a.z >> b.x >> b.y >> b.z;
if (U.isSame(getId(a), getId(b))) cout
L. Wizards Unite
#include
#define ll long long
#define maxn 100100
using namespace std;
ll a[maxn];
int main() {
int t;
scanf("%d", &t);
while (t--) {
int n, k;
scanf("%d%d", &n, &k);
for (int i = 0; i
2020 Petrozavodsk Winter Camp, Jagiellonian U Contest 部分题解
标签:pos init targe 图片 define ret const return mina
原文地址:https://www.cnblogs.com/st1vdy/p/12864857.html

