贝塞尔曲线 WPF MVVM N阶实现公式详解+源代码下载

2021-03-07 07:26

阅读：299

标签：man win dff rri ace contain zip strong onclick

原文:贝塞尔曲线 WPF MVVM N阶实现公式详解+源代码下载

源代码下载

效果图：

技术图片

本程序主要实现：

N阶贝塞尔曲线（通用公式）

本程序主要使用技术

MVVM
InterAction 事件绑定
动态添加Canvas的Item

第一部分公式：

技术图片

n=有效坐标点数量
i=坐标点的下标
P是坐标
t是时间0~1之间

有效坐标点是坐标点的数量减1

计算坐标时分开计算，x，y时分别计算两边

至于括号内上n下i是组合数

计算方法是：技术图片

换成贝塞尔的公式中的组合数是：技术图片

剩下部分应该是很简单了。

因为是求和，所以先是代入公式最后相加即可

例子（摘自百度）

3阶

2阶

现在给出代码的部分

阶乘代码：

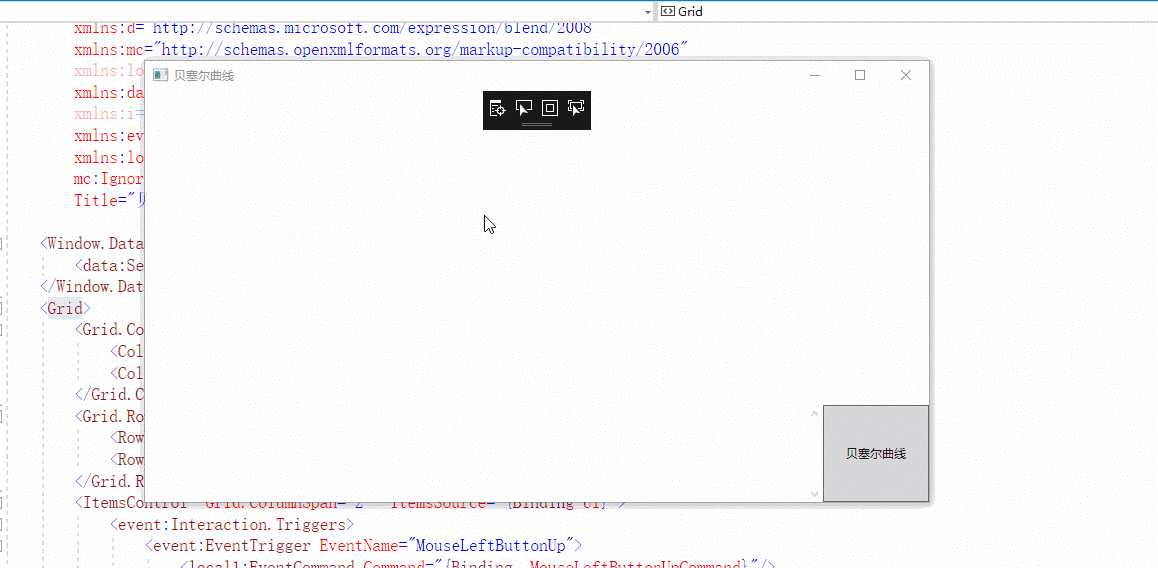
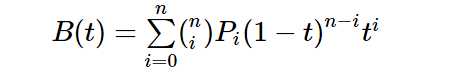
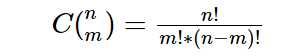
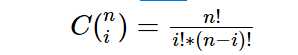
 private int Factorial(int n)
        {
            if (n == 0)
            {
                return 1;
            }
            else
            {
                return n * Factorial(n - 1);
            }

        }

组合数公式代码：

        private int GetCA(int r, int n) => Factorial(r) / (Factorial(n) * Factorial((r - n)));

贝塞尔

  /// 
        /// 求单坐标贝塞尔公式
        /// 
        /// 最大有效坐标点的数量
        /// 需要计算的坐标点的下标
        /// 时间0~1
        /// 单个坐标值（x或者y）
        /// 
        private double GetPoints(int Max, int Index, double Time, double P)
        {
            var C = GetCA(Max, Index);
            var T1 = Math.Pow(Time, Index);
            var T2 = Math.Pow((1 - Time), Max - Index);
            return (C * T1 * T2 * P);
        }

使用方式

  private void SetPoints(Polyline polyline)
        {
            polyline.Points.Clear();
            double ax = 0;
            double ay = 0;
            for (double t = 0.00; t 1.01; t += 0.01)
            {
                for (int i = 0; i )
                {
                    ax += GetPoints(Points.Count - 1, i, t, Points[i].X);
                    ay += GetPoints(Points.Count - 1, i, t, Points[i].Y);
                }
                //此处的ax ay为t时，i下标的有效Points[i].X 坐标点 和Points[i].Y坐标点的Points.Count - 1阶贝塞尔曲线
                polyline.Points.Add(new Point(ax, ay));
                ax = 0;
                ay = 0;
            }
            SetText(polyline.Points);
        }

第二部分 MVVM的事件绑定

MVVM事件绑定需要使用

System.Windwos.Interactiivity.dll

一般来说使用NuGet搜索Expression.Blend.Sdk.WPF就可以了

技术图片

使用方式为

先创建实现 TriggerAction接口类

 public class EventCommand : TriggerAction
    {
        public static readonly DependencyProperty CommandProperty =
       DependencyProperty.Register("Command", typeof(ICommand), typeof(EventCommand),
      null);
        
        public static readonly DependencyProperty CommandParameterProperty =
         DependencyProperty.Register("CommandParameter", typeof(object), typeof(EventCommand),
        null);
     
        public ICommand Command
        {
            get { return (ICommand)GetValue(CommandProperty); }
            set { SetValue(CommandProperty, value); }
        }

        public object CommandParameter
        {
            get { return GetValue(CommandParameterProperty); }
            set { SetValue(CommandParameterProperty, value); }
        }


        protected override void Invoke(object parameter)
        {
            if (this.AssociatedObject != null)
            {
                ICommand command = this.Command;
                if (command != null)
                {
                    if (this.CommandParameter != null)
                    {
                        if (command.CanExecute(this.CommandParameter))
                        {
                            command.Execute(this.CommandParameter);
                        }
                    }
                    else
                    {
                        if (command.CanExecute(parameter))
                        {
                            command.Execute(new Tupleobject, object>(this.AssociatedObject, parameter));
                        }
                    }
                }
            }
        }
        
    }

其次是在XAML页面添加引用

分别为

  
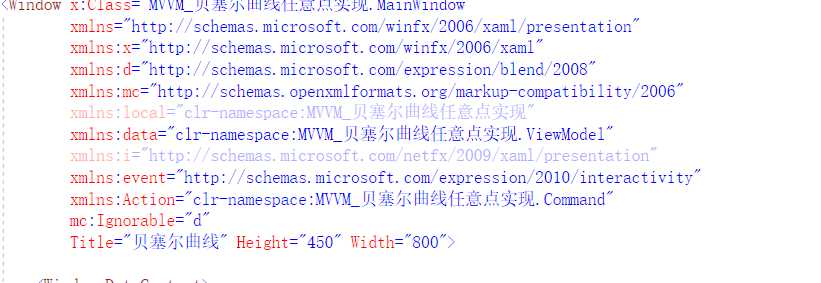
 xmlns:event="http://schemas.microsoft.com/expression/2010/interactivity"
  
xmlns:Action="clr-namespace:MVVM_贝塞尔曲线任意点实现.Command"

技术图片

使用方式：

 ItemsControl  Grid.ColumnSpan="2"  ItemsSource="{Binding UI}">
            event:Interaction.Triggers>
                
                event:EventTrigger EventName="MouseLeftButtonUp">
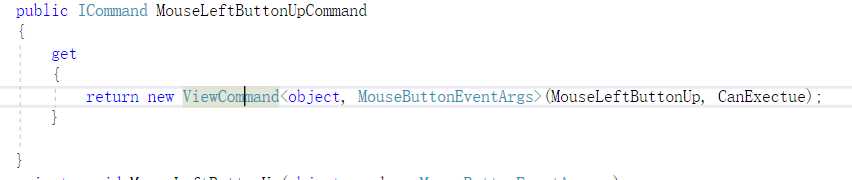
                    Action:EventCommand Command="{Binding  MouseLeftButtonUpCommand}"/>
                event:EventTrigger>
            event:Interaction.Triggers>
            ItemsControl.ItemsPanel>
                ItemsPanelTemplate>
                    Canvas  Background="Transparent"/>
                ItemsPanelTemplate>
            ItemsControl.ItemsPanel>
            ItemsControl.ItemContainerStyle>
                Style>
                    Style>
            ItemsControl.ItemContainerStyle>
            ItemsControl.ItemTemplate>
                DataTemplate>
                    ContentControl Content="{Binding UI}"/>
                DataTemplate>
            ItemsControl.ItemTemplate>
        ItemsControl>

VIewMolde部分则是正常使用即可

技术图片

剩余部分

可以看看源代码

贝塞尔曲线 WPF MVVM N阶实现公式详解+源代码下载

标签：man win dff rri ace contain zip strong onclick

原文地址：https://www.cnblogs.com/lonelyxmas/p/12833999.html

上一篇：WPF ObjectDataProvider

下一篇：WPF 背景网格图

文章来自：搜素材网的编程语言模块，转载请注明文章出处。
文章标题：贝塞尔曲线 WPF MVVM N阶实现公式详解+源代码下载
文章链接：http://soscw.com/index.php/essay/61227.html

亲，登录后才可以留言！

贝塞尔曲线 WPF MVVM N阶实现公式详解+源代码下载

评论

热门文章

推荐文章

最新文章

置顶文章

贝塞尔曲线 WPF MVVM N阶实现 公式详解+源代码下载

评论

热门文章

推荐文章

最新文章

置顶文章

贝塞尔曲线 WPF MVVM N阶实现公式详解+源代码下载