python 二叉树遍历
2021-03-07 20:28
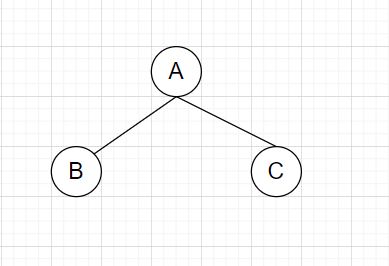
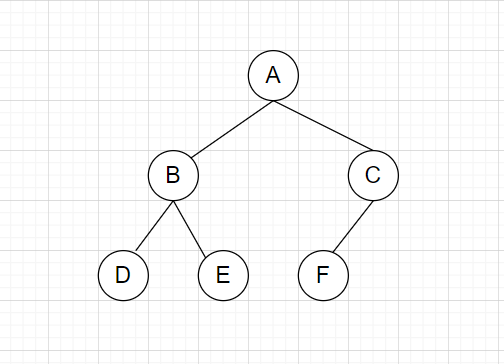
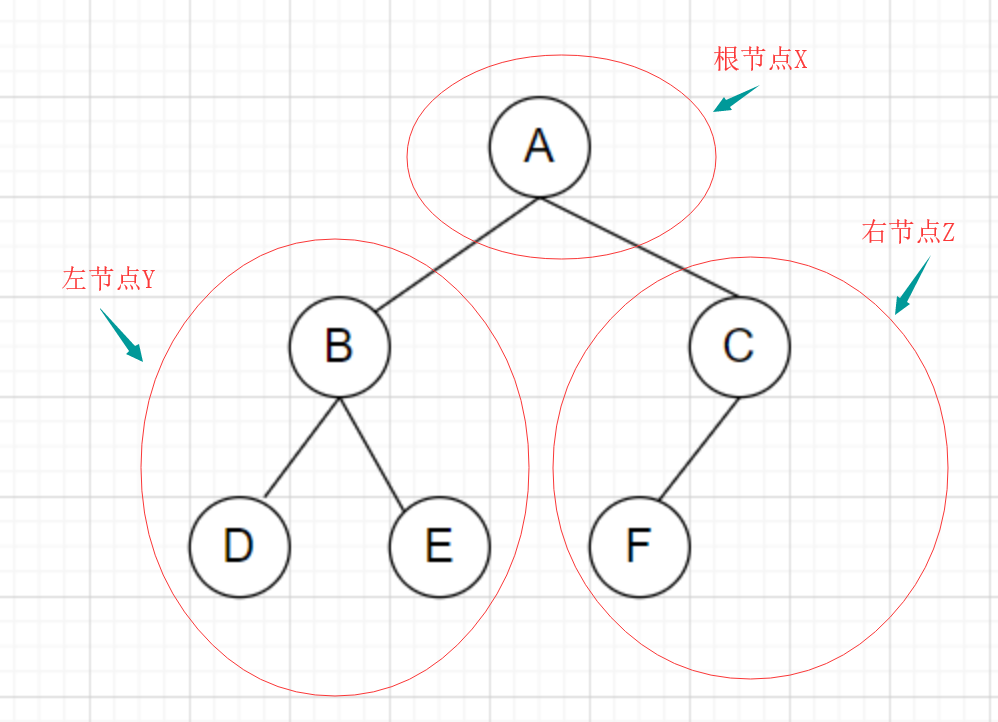
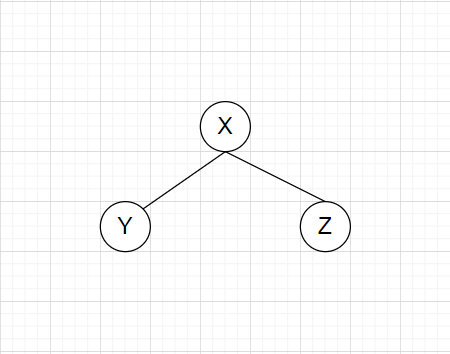
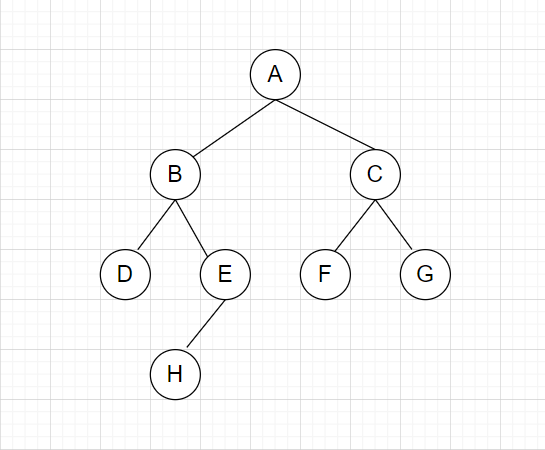
标签:alt smt block 左右 ini 并且 roo 直接 先来 这几天面试老是遇到二叉树遍历问题,之前没怎么吃透,这次尝试好好啃一下,在这记录下这次学习的过程 首先我们先来看二叉树的口述定义 二叉树是树的叶子节点的数量不大于2的树 我们就随便再看看树的口述定义 ? 树是 N (N >= 0 )个结点的有限集合,N = 0 时,称为空树,这是一种特殊情况。在任意一棵非空树中 应满足: ? 1) 有且仅有一个特定的称为根的结点。 ? 2)当 N > 1 时,其余结点可分为 m ( m > 0)个互不相交的有限集合T1 , T2 , T3 , .... Tm ,其中每一个 ? 集合本身又是一棵树,并且称为根结点的子树。 说白了就是类似这样的 二叉树说白了就是一个结点若有子节点,则节点的数量最多为2个 那我们再来复习下满二叉树和完全二叉树 满二叉树就是 一个二叉树,最下面一行的节点没有一个有子节点,其余的每个节点都有二个子节点。 直接看图 完全二叉树就是 一个满二叉树,最后一行,从右向左按顺序去除任意节点后得到的树 就像这样的 满二叉树是完全二叉树的一种特殊的情况 以上是国内对二叉树和完全二叉树的定义,国外的话定义不同 我们来看看国外 第一个的字面翻译过来是满二叉树 第二个的字面完全二叉树 第三个的字面是完美二叉树 在国外定义里面,国内的满二叉树变成了完美二叉树,完全二叉树没有改变 而满二叉树,是一个节点要么有2个叶子节点,要么没有叶子节点 二叉树的遍历主要有以下四种: 前序遍历,中序遍历,后序遍历,广度优先遍历 其中前序遍历,中序遍历和后序遍历可以统称为深度优先遍历(DFS) 这里的前中后主要是根据根节点(叶子节点)的位置来定义的,我们举个简单的例子 我们有如下一个二叉树 根节点为A,左叶子节点为B,右叶子节点为C 按照前中后来遍历 前序遍历:ABC(根节点A在前面) 中序遍历:BAC(根节点A在中间) 后序遍历:BCA(根节点A在最后面) 这里补一句,在不考虑根节点(叶子节点)这几个遍历都是先遍历左节点然后再遍历右节点的 我们再来看看稍微复杂点的二叉树遍历 假设我们有以下一个二叉树结构 我们要对其进行前中后遍历 我们可以这个二叉树添加自定义的名称 比如把A节点作为根节点X BDE作为左节点Y CD作为右节点Z 那么在划分后我们可以把上面的二叉树看成这样的 步骤一 那么前中后遍历分别是 前:XYZ 中:YXZ 后:YZX 左节点Y和右节点Z同样可以看成二叉树 步骤2 对左节点Y进行前中后遍历 前:BDE 中:DBE 后:DEB 步骤3 对右节点Z进行前中后遍历 前:CF 中:FC 后:FC 我们把步骤2和步骤3的结果放到步骤1里面 那么前中后的遍历结果为 前:X(A)Y(BDE)Z(CF) 中:Y(DBE)X(A)Z(FC) 后:Y(DEB)Z(FC)X(A) 最终的结果为: 前:ABDECD 中:DBEAFC 后:DEBFCA 对于其他的二叉树遍历可以按照上面的步骤去理解 假设我们有一个二叉树如下 前:ABDEHCFG 中:DBHEAFCG 后:DHEBFGCA 我们用python实现对二叉树的遍历 首先我们定义一个二叉树 我们以下图二叉树为例来分析下迭代方法的实现 由于先给出根节点,即A节点 先将A节点放入列表中 Node_List -> [A] (注意这个A是代表A这个节点,是TreeNode的实例) 由于列表不为空,进入while循环 首先弹出根节点A,我们将A的值放到储存结构的res列表中 res-> [‘a‘] (我们用‘a‘代表A节点的值) 然后再判断A节点的右节点是否存在,有就放到Node_List里面 Node_List -> [C] 然后我们接着判断A节点的左节点是否存在,由于A节点左边有个B节点,那么将B节点放到Node_List里面 Node_List -> [C,B] 由于Node_List非空 我们再重复上面的步骤,弹出,判断节点是否存在,若有则入表 Node_List -> [C,B]弹出B节点 Node_list -> [C] res -> [‘a‘,‘b‘] Node_List放入B节点的左右节点 Node_List -> [C,E,D] 继续重复 Node_List -> [C,E,D]弹出D节点 Node_List -> [C,E] res -> [‘a‘,‘b‘,‘d‘] 由于D没有左右节点,不进行入表操作 继续重复 Node_List -> [C,E] 弹出E点 Node_List -> [C] res -> [‘a‘,‘b‘,‘d‘,‘e‘] 由于E点没有左右节点 不进行入表操作 继续重复 Node_List -> [C] 弹出C点 Node_List -> [] res -> [‘a‘,‘b‘,‘d‘,‘e‘,‘c‘] 由于C点有F节点,入表 Node_List -> [F] 继续重复 Node_List -> [F] 弹出F点 Node_List -> [] res -> [‘a‘,‘b‘,‘d‘,‘e‘,‘c‘,‘f‘] 由于F点没有左右节点 Node_List为空,结束while循环 我们来分析下 一开始 root非空,Node_List为空,进入while循环 由于root非空,进入if语句 Node_List -> [A] root指向B 由于Node_List非空,继续while循环 由于A的左节点存在 继续if循环 Node_List -> [A B] 由于Node_List非空,继续while循环 由于B的左节点存在 继续if循环 Node_List -> [A,B,D] root指向D的左节点 由于Node_List非空,继续while循环 由于 D的左节点不存在 进入else循环 Node_List ->[A,B,D]弹出D节点 Node_List ->[A,B] res ->[‘d‘] 把root指向D的右节点 由于Node_List非空,继续while循环 由于D的右节点不存在,进入else语句 Node_List ->[A,B] 弹出B节点 Node_List -> [A] res -> [‘d‘,‘b‘] 将root指向B的右节点 由于Node_List非空,继续while循环 由于B的右节点存在,进入if语句 Node_List ->[A] 将E节点放入Node_List Node_List -> [A,E] 把root指向E的左节点 继续重复。。。,这里就不写了 这个遍历和前序遍历的迭代方法很像 首先我们要明白对最简单的二叉树ABC的后续遍历是BCA BCA=ACB[::-1] 我们只需要求出ACB就能得到ABC的后序遍历了 只需在添加左右节点的时候改变下顺序即可 python 二叉树遍历 标签:alt smt block 左右 ini 并且 roo 直接 先来 原文地址:https://www.cnblogs.com/cofish/p/14255258.html
二叉树的定义
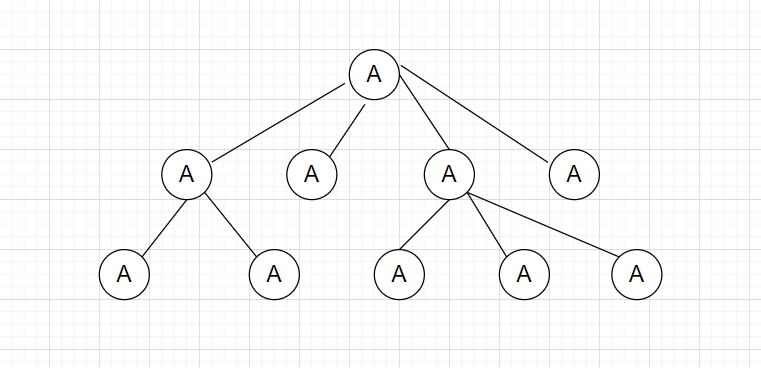
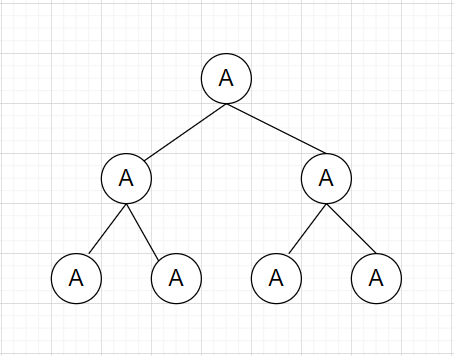
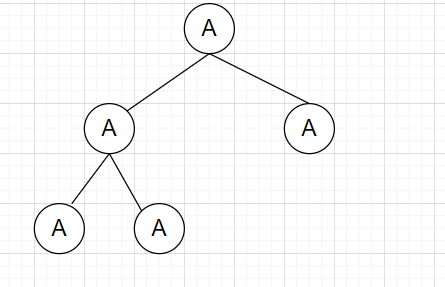
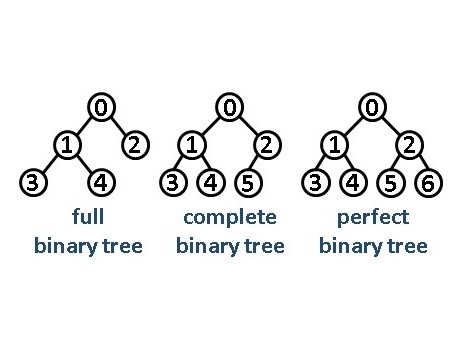
二叉树的遍历
二叉树遍历的实现
class TreeNode(object):
def __init__(self,val):
self.val=val
self.left=None
self.right=None
前序遍历
递归实现
res=[]
def pre_order(root:TreeNode):
#定义函数结束条件
if not root:
return
res.append(root.val)
#对左边的结构
pre_order(root.left)
#对右边的结构
pre_order(root.right)
迭代实现
res=[]
def preorder(root:TreeNode):
if not root:
return
node_list=[root]
while node_list:
node_popped=node_list.pop()
res.append(node_popped.val)
if node_popped.right:
node_list.append(node_popped.right)
if node_popped.left:
node_list.append(node_popped.left)

中序遍历
递归实现
res=[]
def mid_order(root:TreeNode):
if not root:
return
mid_order(root.left)
res.append(root.val)
mid_order(root.right)
迭代实现
res=[]
def mid_order(root:TreeNode):
if not root:
return
node_list=[]
while node_list or root:
if root:
node_list.append(root)
root=root.left
else:
root = node_list.pop()
res.append(root.val)
root=root.right

后序遍历
递归实现
res=[]
def back_order(root:TreeNode):
if not root:
return
back_order(root.left)
back_order(root.right)
res.append(root)
迭代实现
res=[]
def back_order(root:TreeNode):
if not root:
return
node_list=[root]
while node_list:
pop_=node_list.pop()
res.append(pop_.val)
if pop_.left:
node_list.append(pop_.left)
if pop_.right:
node_list.append(pop_.right)
real_ans=res[::-1]
广度优先遍历
迭代实现
res=[]
def BFS(root:TreeNode):
if not root:
return
node_list=[root]
while node_list:
pop_=node_list.pop(0)
res.append(pop_.val)
if pop_.left:
node_list.append(pop_.left)
if pop_.right:
node_list.append(pop_.right)