回溯算法:求子集问题(二)
2021-03-08 11:28
标签:amp mamicode 集合 track 一个 public tin int start 详细 ? 给定一个可能包含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。 说明:解集不能包含重复的子集。 示例: 思路 这道题目和回溯算法:求子集问题!区别就是集合里有重复元素了,而且求取的子集要去重。 那么关于回溯算法中的去重问题,「在40.组合总和II中已经详细讲解过了,和本题是一个套路」。 「剧透一下,后期要讲解的排列问题里去重也是这个套路,所以理解“树层去重”和“树枝去重”非常重要」。 用示例中的[1, 2, 2] 来举例,如图所示:(「注意去重需要先对集合排序」) 本题就是其实就是回溯算法:求子集问题!的基础上加上了去重,去重我们在回溯算法:求组合总和(三)也讲过了,所以我就直接给出代码了: C++代码 总结 「就酱,如果感觉融会贯通了,就把「代码随想录」介绍给自己的同学朋友吧,也许他们也需要!」 回溯算法:求子集问题(二) 标签:amp mamicode 集合 track 一个 public tin int start 详细 原文地址:https://blog.51cto.com/15069438/2576407
?
通知:我将公众号文章和学习相关的资料整理到了Github :https://github.com/youngyangyang04/leetcode-master,方便大家在电脑上学习,可以fork到自己仓库,顺便也给个star支持一波吧!
第90题.子集II
题目链接:https://leetcode-cn.com/problems/subsets-ii/
输入: [1,2,2]
输出:
[
[2],
[1],
[1,2,2],
[2,2],
[1,2],
[]
]
做本题之前一定要先做78.子集。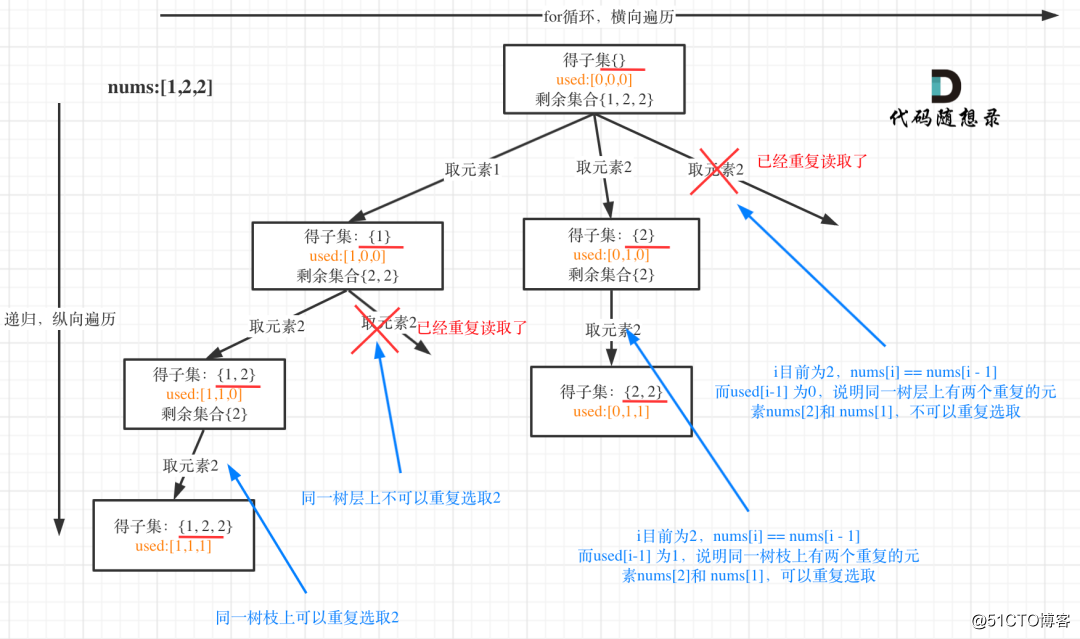
从图中可以看出,同一树层上重复取2 就要过滤掉,同一树枝上就可以重复取2,因为同一树枝上元素的集合才是唯一子集!
class Solution {
private:
vector
其实这道题目的知识点,我们之前都讲过了,如果之前讲过的子集问题和去重问题都掌握的好,这道题目应该分分钟AC。
上一篇:回溯算法:递增子序列
下一篇:本周小结!(回溯算法系列二)