算法基础<二>

标签：exe   就是   strong   less   优先   算法   elm   dispose   prim   

堆

堆：当一棵二叉树的每个结点都大于等于它的两个子结点时，它被称为堆有序。

命题O:根结点是堆有序的二叉树中的最大结点

二叉堆：一组能够用堆有序的完全的二叉树排序的元素，并在数组中按照层级存储（不使用数组的第一个位置）。

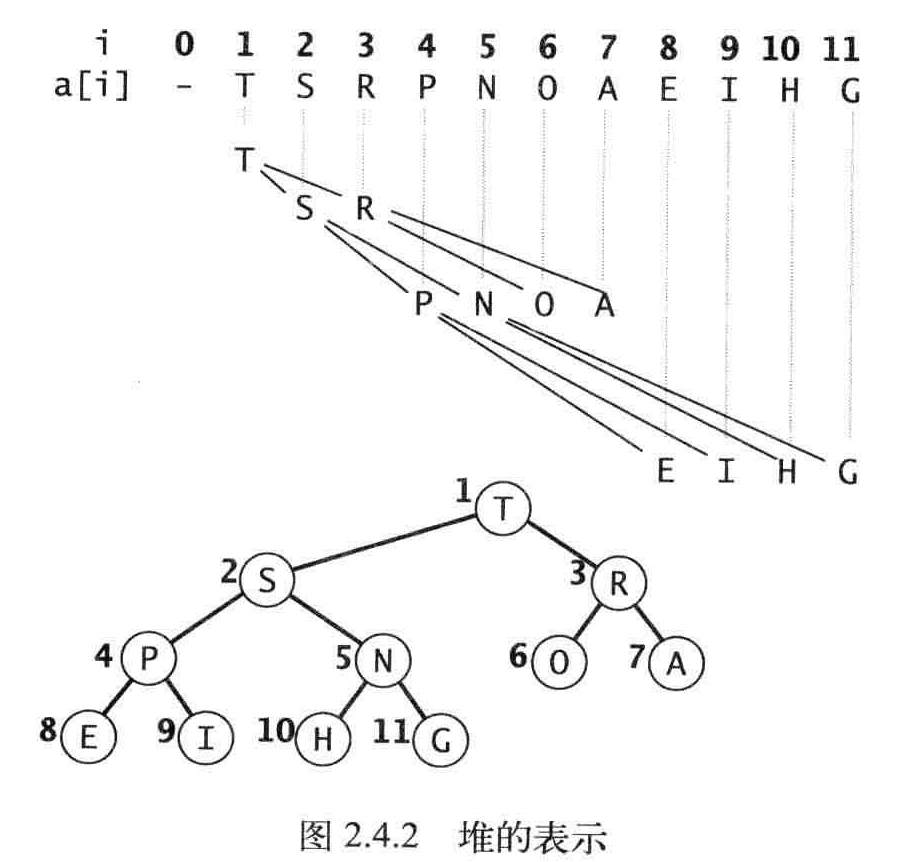
命题P:一棵大小为N的完全二叉树的高度为lgN。

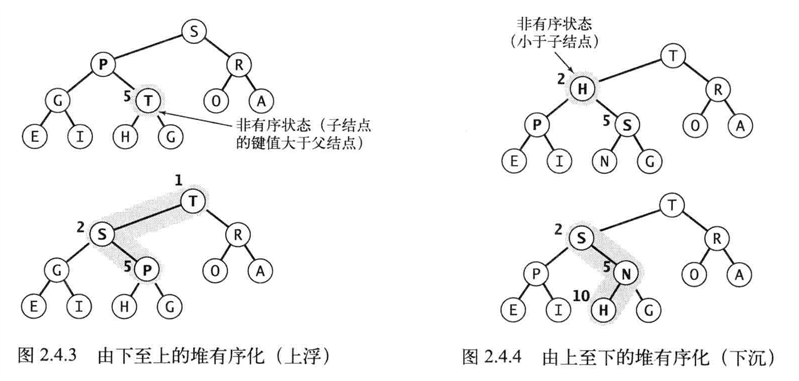
堆有序上浮

由下至上的堆有序（上浮）实现

private void swim(int k)
{
	while(k>1&&less(k/2,k))
	{
		exch(k/2,k);
		k=k/2;
	}
}

堆有序下沉

由上至下的堆有序（下沉）实现。

命题R:用下沉操作由N个元素构造堆只需少于2N次比较以及小于N次交换。

private void sink(int k)
{
	while(2*k 

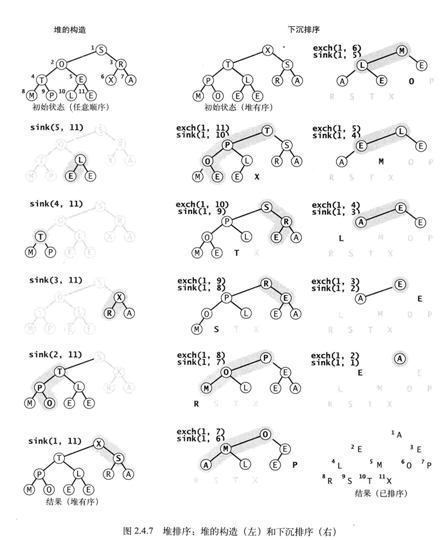
堆有序排序

    public class HeapSortNet where TItem : IComparable
    {
		///注意这边有一个Bug忽略了数组的第一个元素。下面的优先队列消除了这个Bug
        public static void Sort(TItem[] items)
        {
            int n = items.Length;
            // 左边堆构造
            for (int k = n / 2; k >= 1; k--)
                Sink(items, k, n);//K的值需要比N的大
            // 右边堆排序
            while (n > 1)
            {
                Exch(items, 1, n--);//将最大的放到最后
                Sink(items, 1, n);//将最大之前的那个找出来放到第一个
            }
        }
        /// 

        /// 下沉
        /// 
        /// 
        /// 
        /// 
        private static void Sink(TItem[] items, int k, int n)
        {
            while (2 * k 

命题S:将N个元素排序，堆排序只需要少于（2NlgN+2N）次比较（以及一半次数的交换）

改进：大多数在下沉排序期间重新插入堆的元素会被直接加入到堆底。

Floyd在1964年观察发现，可以通过免去检查元素是否到达正确位置来节省时间，

下沉中总是直接提升较大的子节点直至到达堆底，然后再使元素上浮到正确的位置，可以将比较次数减少一半

唯一能够同时最优地利用空间和时间的方法，最坏情况下也能保证~2NlgN次比较和恒定的额外空间。在嵌入式或底成本的移动设备中很流行，无法利用缓存，很少于其他元素进行比较。

优先队列

就是用堆的方式排列的数组。支持查找最大最小元素和插入元素

最大优先队列

最大优先队列：支持删除最大元素和插入元素

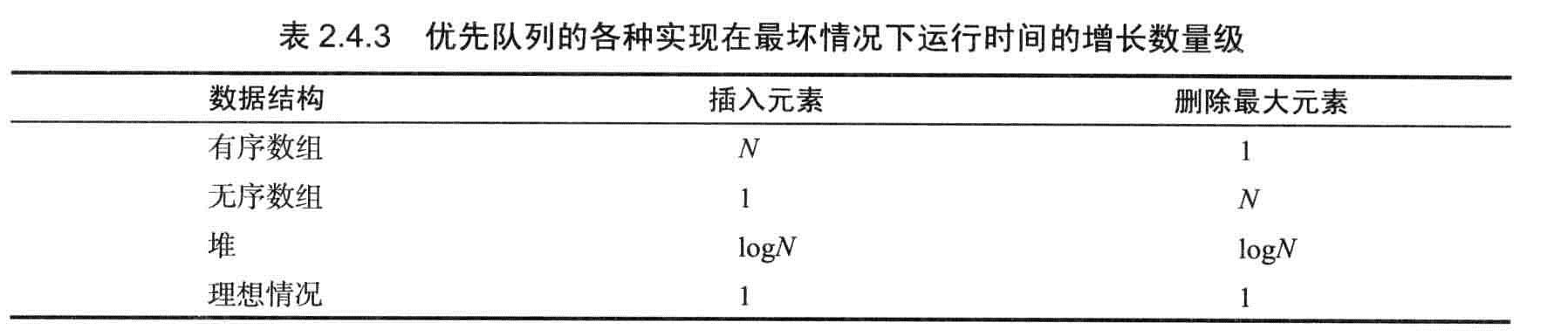
基于堆的优先队列：存储在数组[1……N]中，数组[0]没有使用。

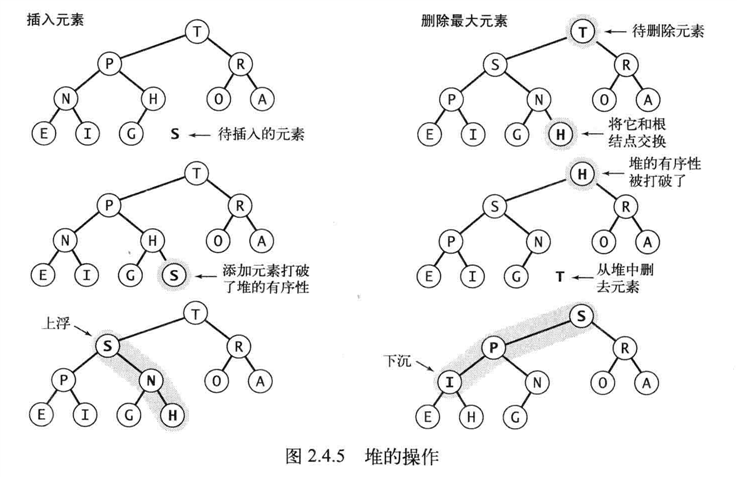
命题Q:对于一个含有N个元素的基于堆的优先队列，插入元素操作只需要不超过（lgN+1）次比较，删除最大元素的操作需要不超过2lgN次比较。

    /// 

    /// 优先队列
    /// 
    /// 
    public interface IMaxHeapQueue : IEnumerable, IDisposable
    {
        bool IsEmpty { get; }
        int Length { get; }
        void Insert(TItem x);
        TItem DeleteMax();
        TItem Max();
    }

?

    public class MaxPQNet : IMaxHeapQueue where TItem : IComparable
    {
        private TItem[] _items;
        private int _length;
        private IComparer _comparer;
        public MaxPQNet(int capacity)
        {
            _items=new TItem[capacity+1];
            _length = 0;
        }

        public MaxPQNet():this(1)
        {

        }

        public MaxPQNet(int capacity, IComparer comparer):this(capacity)
        {
            _comparer = comparer;
        }


        public MaxPQNet(TItem[]  items)
        {
            _length = items.Length;
            _items = new TItem[items.Length + 1];
            for (int i = 0; i = 1; k--)
                sink(k);
        }

        private void sink(int k)
        {
            while (k*2 1 && less(k / 2, k))
            {
                exch(k,k/2);
                k = k / 2;
            }
        }
        private bool less(int i, int j)
        {
            if (_comparer == null)
            {
                return _items[i].CompareTo(_items[j])  GetEnumerator()
        {
            if (!IsEmpty)
            {
                var temitem = new TItem[_length-1];
                for (int i = 0; i (temitem);

                while (!temmaxpq.IsEmpty())
                {
                    yield return temmaxpq.DelMax();
                }
            }
            

        }

        IEnumerator IEnumerable.GetEnumerator()
        {
            return GetEnumerator();
        }
        protected  virtual void Dispose(bool disposing)
        {
            if (disposing)
            {
                if (!IsEmpty)
                {
                    for (int i = 1; i  Length == 0;
        public int Length => _length;
        public void Insert(TItem item)
        {
            if(_length==_items.Length-1) resize(_length*2);
            _items[++_length] = item;
            swim(_length);
        }

        public TItem DeleteMax()
        {
            if (IsEmpty) return default;
            var item = _items[1];
            exch(1,_length--);//把最小值交换到第一个重新堆排序
            _items[_length + 1] = default;
            sink(1);
            if(_length>0&&_length==(_items.Length-1)/4) resize(_items.Length/2);
            return item;
        }

        public TItem Max()
        {
            if (IsEmpty)
                return default;
            return _items[1];
        }
    }

堆上优先队列

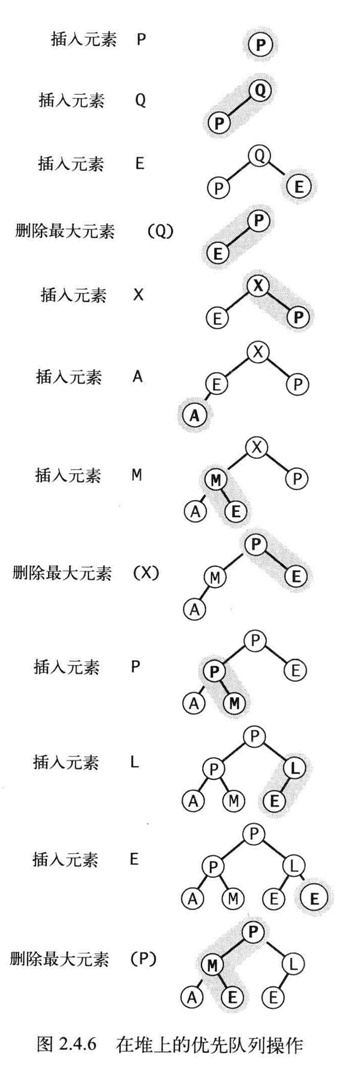
最小优先队列

根结点是最小值，其他相同

    public class MinPQNet : IMinHeapQueue where TItem : IComparable
    {
        private TItem[] _items;
        private int _length;
        private IComparer _comparer;
        public MinPQNet(int capacity)
        {
            _items = new TItem[capacity + 1];
            _length = 0;
        }

        public MinPQNet() : this(1)
        {

        }

        public MinPQNet(int capacity, IComparer comparer) : this(capacity)
        {
            _comparer = comparer;
        }


        public MinPQNet(TItem[] items)
        {
            _length = items.Length;
            _items = new TItem[items.Length + 1];
            for (int i = 0; i = 1; k--)
                sink(k);
        }

        private void sink(int k)
        {
            while (k * 2  1 && greater(k / 2, k))
            {
                exch(k, k / 2);
                k = k / 2;
            }
        }

        private bool greater(int i, int j)
        {
            if (_comparer == null)
            {
                return _items[i].CompareTo(_items[j]) > 0;
            }
            else
            {
                return _comparer.Compare(_items[i], _items[j]) > 0;
            }
        }

        private void exch(int i, int j)
        {
            var item = _items[i];
            _items[i] = _items[j];
            _items[j] = item;
        }

        private void resize(int capacity)
        {
            if (capacity  GetEnumerator()
        {
            if (!IsEmpty)
            {
                var temitem = new TItem[_length - 1];
                for (int i = 0; i (temitem);

                while (!temmaxpq.IsEmpty())
                {
                    yield return temmaxpq.DelMin();
                }
            }


        }

        IEnumerator IEnumerable.GetEnumerator()
        {
            return GetEnumerator();
        }
        protected virtual void Dispose(bool disposing)
        {
            if (disposing)
            {
                if (!IsEmpty)
                {
                    for (int i = 1; i  Length == 0;
        public int Length => _length;
        public void Insert(TItem item)
        {
            if (_length == _items.Length - 1) resize(_length * 2);
            _items[++_length] = item;
            swim(_length);
        }

        public TItem DeleteMin()
        {
            if (IsEmpty) return default;
            var item = _items[1];
            exch(1, _length--);//把最小值交换到第一个重新堆排序
            _items[_length + 1] = default;
            sink(1);
            if (_length > 0 && _length == (_items.Length - 1) / 4) resize(_items.Length / 2);
            return item;
        }

        public TItem Min()
        {
            if (IsEmpty)
                return default;
            return _items[1];
        }
    }

索引优先队列

可以快速访问已经插入队列中的项。

不会改变插入队列中项的数据结构

命题Q(续):在一个大小为N的索引优先队列中，插入(insert)元素，改变优先级，删除，删除最小元素和删除最大元素操作所需要的比较次数和LogN成正比。

示例为最大索引优先队列，简单改写就可以变成最小索引优先队列

   /// 

    /// 增加一个key，key对应一个索引，实际交换排序是控制key对应的索引
    /// 
    /// 
    public class KeyMaxPQNet : IMaxKeyHeap where TItem:IComparable
    {

        private int _length;
        private int _capacity;
        /// 

        /// key对应的索引
        /// 
        private int[] _keysIndex;
        /// 

        /// 索引对应的key
        /// 
        private int[] _indexesKey;
        /// 

        /// key对应的item
        /// 
        private TItem[] _items;
        public bool IsEmpty => _length == 0;

        public int Length => _length;

        public int Capacity => _capacity;

        public KeyMaxPQNet(TItem[] items)
        {
            if (items == null || !items.Any()) throw new ArgumentNullException("items is empty");
            _length = 0;
            _capacity = items.Length;
            _items = new TItem[_capacity + 1];
            _keysIndex = new int[_capacity + 1];
            _indexesKey = new int[_capacity + 1];
            for (int i = 0; i 
        /// if Empty,throw exception
        /// 
        /// 
        public TItem DeleteMax()
        {
            if (IsEmpty) throw new NullReferenceException("this is empty queue");
            int max = _indexesKey[1];
            var item = _items[max];
            exch(1,_length--);
            sink(1);
            _keysIndex[max] = -1;
            _items[max] = default;
            _indexesKey[_length + 1] = -1;
            return item;
        }

        public void Delete(int key)
        {
            validateKey(key);
            if(!Contains(key)) throw new ArgumentException("this index is not in this queue");
            var k = _keysIndex[key];
            exch(k,_length--);//这边已经排除最后一项
            swim(k);
            sink(k);
            _items[key] = default;
            _keysIndex[key] = -1;

        }
        public void Replace(int key, TItem item)
        {
            validateKey(key);
            if(!Contains(key)) throw new NullReferenceException("this key not in queue");
            _items[key] = item;
            swim(_keysIndex[key]);
            sink(_keysIndex[key]);
        }


        public TItem KeyOf(int key)
        {
            validateKey(key);
            if(!Contains(key)) return default;
            return _items[key];

        }

        public int MaxKey()
        {
            if(IsEmpty)
                throw new ArgumentException("this is null queue");
            return _indexesKey[1];
        }

        public TItem Max()
        {
            if(IsEmpty)
                throw new ArgumentException("this is null queue");
            return _items[_indexesKey[1]];
        }
        public bool Contains(int key)
        {
            validateKey(key);
            return _keysIndex[key] != -1;
        }

        public IEnumerator GetEnumerator()
        {
            if (!IsEmpty)
            {
                var queue=new KeyMaxPQNet(_items);
                for (int i = 1; i  _capacity) throw new ArgumentException("this key is invalid");
        }

        private void swim(int index)
        {
            while (index>1 && less(index/2,index))
            {
                exch(index, index / 2);
                index = index / 2;
            }
        }

        private void sink(int index)
        {
            while (2 * index 

排序算法应用

多向并归

索引优先队列用例解决多向归并问题：它将多个有序的输入流归并成一个有序的输出流。

输入可能来自于多种科学仪器的输出（按时间排序）

多个音乐网站或电影网站的信息列表（名称或艺术家名字）

商业交易（按时间排序）

使用优先队列，无论输入有多长都可以把它们全部读入并排序

交易数据按照日期排序

商业计算

信息搜索

运筹学：调度问题，负载均衡

事件驱动模拟

数值计算：浮点数来进行百万次计算，一些数值的计算使用优先队列和排序来计算精确度，曲线下区域的面积，数值积分方法就是使用一个优先队列来存储一组小间隔中每段的近似精确度。积分的过程就是山区精确度最低的间隔并将其分为两半。

组合搜索：一组状态演化成另一组状态可能的步骤和步骤的优先级。

Prim算法和Dijkstra算法:

Kruskal算法:

霍夫曼压缩：

字符串处理：

排序特点

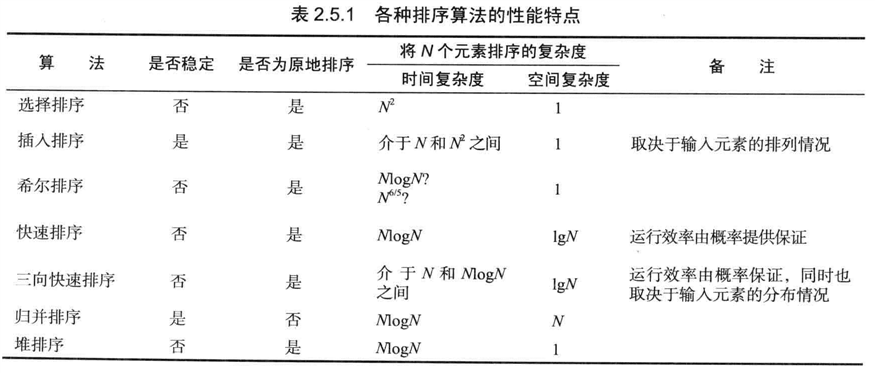
性质T:快速排序是最快的通用排序算法。

对原始数据类型使用（三向切分）快速排序，对引用类型使用归并排序。

命题U:平均来说，基于切分的选择算法的运行时间是线性级别的。

算法基础

标签：exe   就是   strong   less   优先   算法   elm   dispose   prim   

原文地址：https://www.cnblogs.com/lovexinyi/p/14126838.html