Prim 算法(浙江大学数据结构 陈越老师) 完整实现(含测试)

标签：else   相等   测试   包含   lan   版本   有向图   父节点   无向图   

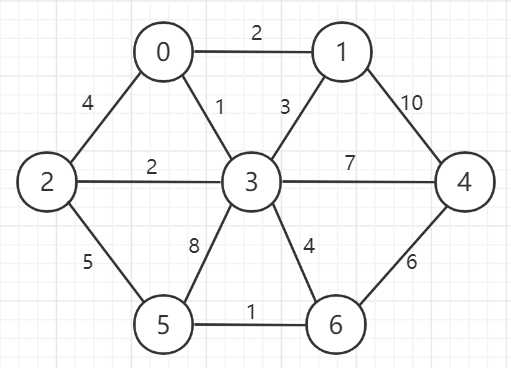
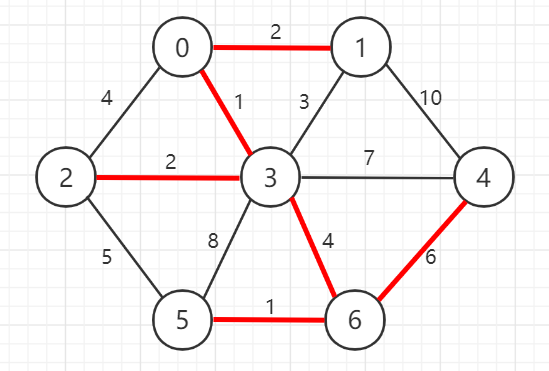
根据上图, 构造出来的最小生成树的权值和应为 16.

主要部分代码:

/**
 * 将最小生成树保存为邻接表存储的图 MST, 返回最小权重和
 * @param Graph
 * @param MST 即 Minimun-cost Spanning Tree 最下生成树
 * @return
 */
int Prim(MGraph Graph, LGraph * MST)
{
    WeightType dist[MaxVertexNum], TotalWeight;
    Vertex parent[MaxVertexNum], V, W;
    int VCount;
    Edge E;

    // 初始化. 默认初始点下标是 0
    for (V = 0; V Nv; V++)
    {
        // 这里假设若 V 到 W 没有直接的边, 则 Graph->G[V][W] 定义为 INFINITY
        dist[V] = Graph->G[0][V]; // 初始时 dist 数组中的值设置为顶点 0 与 其它顶点之间的边的权重
        parent[V] = 0; // 暂且定义所有顶点的父节点都是初始点 0
    }
    TotalWeight = 0; // 初始化权重和
    VCount = 0; // 初始化收录的顶点数
    // 创建包含所有顶点但没有边的图. 注意用邻接表版本
    *MST = CreateLGraph(Graph->Nv);
    E = (Edge)malloc(sizeof(struct ENode)); // 建立空的边节点

    // 将初始点 0 收录进 MST
    dist[0] = 0;
    VCount++;
    parent[0] = -1; // 当前树根是 0

    while (1)
    {
        V = FindMinDist(Graph, dist);
        // 未被收录顶点中 dist 最小者
        if (V == ERROR) // 若这样的 V 不存在
            break;

        // 将 V 及相应的边  收录进 MST
        E->V1 = parent[V];
        E->V2 = V;
        E->Weight = dist[V];
        InsertLEdge(*MST, E);
        TotalWeight += dist[V];
        dist[V] = 0;
        VCount++;


        for (W = 0; W Nv; W++) // 对图中的每个节点
        {
            if (dist[W] != 0 && Graph->G[V][W] G[V][W] G[V][W]; // 更新 dist[W]
                    parent[W] = V; // 更新树
                }
            }
        }
    } // while 结束

    /* 测试 */
    // PrintLGraph(*MST);
    /* 测试 */

    if (VCount Nv) // MST 中收录的顶点不到 |V| 个
        TotalWeight = ERROR;
    return TotalWeight; // 算法执行完毕, 返回最小权重或错误标记
}

/**
 * 返回未被收录顶点中 dist 最小者
 * @param Graph
 * @param dist
 * @return
 */
Vertex FindMinDist(MGraph Graph, WeightType dist[])
{
    Vertex MinV, V; // Min 表示 dist 中的最小者, V 是临时变量
    WeightType MinDist = INFINITY; // 用来存储顶点 dist 最小的值

    for (V = 0; V Nv; V++)
    {
        if (dist[V] != 0 && dist[V] 

按 : 这里的代码主要是参考了《数据结构》(第2版 陈越) 图那一章的代码. 略有改动.

完整实现及测试

#include 
#include 
#include 
#include 
#include "queue.h"

#define ERROR -1

/*---------- 邻接矩阵和邻接表的公共部分 ----------*/
#define MaxVertexNum 100 // 最大顶点数设为 100
#define INFINITY 65535 // 无穷大设为双字节无符号整数的最大值 65535
typedef int Vertex; // 用顶点下标表示顶点, 为整型
typedef int WeightType; // 边的权值设为整型
typedef char DataType; // 顶点存的数据类型设为字符型

// 全局变量 Visited[], 初始化为 false
bool Visited[MaxVertexNum]; // 0 代表 false, 1 代表 true

static void init()
{
    memset(Visited, 0, MaxVertexNum);
}

// 边的定义
typedef struct ENode * PtrToENode;
struct ENode {
    Vertex V1, V2; // 有向边 
    WeightType Weight; // 权重
};
typedef PtrToENode Edge;

void Visit(Vertex V)
{
    printf("正在访问顶点%d\n", V);
}
/*---------- 邻接矩阵和邻接表的公共部分 ----------*/


/*---------- 邻接矩阵方式存储图 ----------*/
#define MaxSize 100 // 创建空队列时用到, 代表空队列的数组的最大长度

// 图节点的定义
typedef struct MGNode * PtrToMGNode;
struct MGNode {
    int Nv; // 顶点数
    int Ne; // 边数
    WeightType G[MaxVertexNum][MaxVertexNum]; // 邻接矩阵
    DataType Data[MaxVertexNum]; // 存顶点的数据
    /* 注意: 若顶点无数据, 此时 Data[] 可以不用出现 */
};
typedef PtrToMGNode MGraph;


MGraph CreateMGraph(int VertexNum)
{
    // 初始化一个有 VertexNum 个顶点但没有边的图
    Vertex V, W;
    MGraph Graph;

    Graph = (MGraph) malloc(sizeof(struct MGNode)); // 建立图
    Graph->Nv = VertexNum;
    Graph->Ne = 0;
    // 初始化邻接矩阵, 并设置所有的边的权值为 INFINITY
    // 注意: 这里默认顶点编号是从 0 开始, 到 (Graph->Nv - 1)
    for (V = 0; V Nv; V++)
        for (W = 0; W Nv; W++)
            Graph->G[V][W] = INFINITY;

    return Graph;
}

void InsertMEdge(MGraph Graph, Edge E)
{
    // 插入边 
    Graph->G[E->V1][E->V2] = E->Weight;
    // 若是无向图, 还要插入边 
    Graph->G[E->V2][E->V1] = E->Weight;
}

MGraph BuildMGraph()
{
    MGraph Graph;
    Edge E;
    // Vertex V;
    int Nv, i;

    scanf("%d", &Nv); // 读入顶点个数
    Graph = CreateMGraph(Nv); // 初始化有 Nv 个顶点但没有边的图

    scanf("%d", &(Graph->Ne)); // 读入边数
    if (Graph->Ne != 0) // 如果有边
    {
        E = (Edge)malloc(sizeof(struct ENode)); // 建立边节点
        // 读入边, 格式为 "起点 终点 权重", 插入邻接矩阵
        for (i = 0; i Ne; i++) {
            scanf("%d %d %d", &E->V1, &E->V2, &E->Weight);
            // 注意: 如果权重不是整型, Weight 的读入格式要改
            InsertMEdge(Graph, E);
        }
    }
    // 如果顶点有数据的话, 读入数据
    /*for (V = 0; V Nv; V++)
        scanf("%c", &(Graph->Data[V]));*/

    return Graph;
}

// 简单遍历图
void PrintMGraph(MGraph G)
{
    int i, j;

    for (i = 0; i Nv; i++)
    {
        for (j = 0; j Nv; j++)
        {
            if (G->G[i][j] == INFINITY)
            {
                printf("∞ ");
                continue;
            }
            printf("%d ", G->G[i][j]);
        }
        printf("\n");
    }
}

// 判断是否是邻接矩阵图的边
bool IsMEdge(MGraph Graph, Vertex V, Vertex W)
{
    return Graph->G[V][W] Nv; W++) // 对图中的每个顶点
        {
            // 若 W 是 V 的邻接点并且未访问过
            if (!Visited[W] && IsMEdge(Graph, V, W)) {
                // 访问顶点 W
                Visit(W);
                Visited[W] = true; // 标记 W 已访问
                AddQ(Q, W); // W 入队
            }
        }
    }
}
/*---------- 邻接矩阵方式存储图 ----------*/

/*-------------------------------------------------------------------------------------------*/

/*---------- 邻接表方式存储图 ----------*/
// 邻接点的定义
typedef struct AdjVNode *PtrToAdjVNode; // Adjacency list --> 邻接表
struct AdjVNode
{
    Vertex AdjV; // 邻接点下标
    WeightType Weight; // 边权重
    PtrToAdjVNode Next; // 指向下一个邻接点的指针
};

// 顶点表头节点的定义
typedef struct VNode
{
    PtrToAdjVNode FirstEdge; // 边表头指针
    DataType Data; // 存顶点的数据
    // 注意, 很多情况下, 顶点无数据, 此时 Data 可以不用出现
} AdjList[MaxVertexNum]; // AdjList 是邻接表类型

// 图节点的定义
typedef struct LGNode *PtrToLGNode;
struct LGNode
{
    int Nv; // 顶点数
    int Ne; // 边数
    AdjList G; // 邻接表, 用数组方式存储每一个顶点的表头节点
};
typedef PtrToLGNode LGraph; // 以邻接表的方式存储的图类型

// 初始化一个有 VertexNum 个顶点但没有边的图
LGraph CreateLGraph(int VertexNum)
{
    Vertex V;
    LGraph Graph;

    Graph = (LGraph) malloc(sizeof(struct LGNode)); // 建立图
    Graph->Nv = VertexNum; // 顶点数为 VertexNum
    Graph->Ne = 0; // 边数为 0
    // 初始化邻接表头指针
    // 注意: 这里默认顶点编号从 0 开始, 到(Graph->Nv - 1)
    for (V = 0; V Nv; V++)
        Graph->G[V].FirstEdge = NULL;

    return Graph;
}

// 插入边, LEdge 中的 L 表示是邻接表
void InsertLEdge(LGraph Graph, Edge E)
{
    PtrToAdjVNode NewNode;
    // 插入边 
    // 为 V2 建立新的邻接点
    NewNode = (PtrToAdjVNode) malloc(sizeof(struct AdjVNode));
    NewNode->AdjV = E->V2;
    NewNode->Weight = E->Weight;
    // 将 V2 插入 V1 的表头(插入表头比插入表尾明显容易实现)
    NewNode->Next = Graph->G[E->V1].FirstEdge;
    Graph->G[E->V1].FirstEdge = NewNode;

    // 若是无向图, 还有插入边 
    // 为 V1 建立新的邻接点
    NewNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
    NewNode->AdjV = E->V1;
    NewNode->Weight = E->Weight;
    // 将 V1 插入 V2 的表头
    NewNode->Next = Graph->G[E->V2].FirstEdge;
    Graph->G[E->V2].FirstEdge = NewNode;
}

// 建图
LGraph BuildLGraph()
{
    LGraph Graph;
    Edge E;
    // Vertex V;
    int Nv, i;

    scanf("%d", &Nv); // 读入顶点个数
    Graph = CreateLGraph(Nv); // 初始化有 Nv 个顶点但没有边的图

    scanf("%d", &(Graph->Ne)); // 读入边数
    if (Graph->Ne != 0)
    { // 如果有边
        E = (Edge) malloc(sizeof(struct ENode));
        // 读入边, 格式为 "起点, 终点, 权重", 插入邻接表
        for (i = 0; i Ne; i++)
        {
            scanf("%d %d %d", &E->V1, &E->V2, &E->Weight);
            // 注意: 如果权重不是整型, Weight 的读入格式要改
            InsertLEdge(Graph, E);
        }
    }

    // 如果顶点有数据的话, 读入数据
    /*for (V = 0; V Nv; V++)
    {
        scanf("%c", &(Graph->G[V].Data));
    }*/

    return Graph;
}

// 简单遍历图
void PrintLGraph(LGraph Graph)
{
    if (!Graph->G[0].FirstEdge) // 邻接表为空
        return;

    int i;
    for (i = 0; i Nv; i++)
    {
        printf("%d: | ", i);

        PtrToAdjVNode tmp = Graph->G[i].FirstEdge;

        while (tmp)
        {
            printf("%d %d | ", tmp->AdjV, tmp->Weight);
            tmp = tmp->Next;
        }
        printf("\n");
    }
}


// Visited[] 为全局变量， 已经初始化为 false
// 以 V 为出发点对邻接表存储的图 Graph 进行 DFS 搜索
void DFS(LGraph Graph, Vertex V, void(*Visit)(Vertex))
{
    PtrToAdjVNode W;

    Visit(V); // 访问第 V 个顶点
    Visited[V] = 1; // 标记 V 已访问

    for (W = Graph->G[V].FirstEdge; W; W = W->Next) // 对 V 的每个邻接点 W->AdjV
        if (!Visited[W->AdjV]) // 若 W->AdjV 为被访问
            DFS(Graph, W->AdjV, Visit); // 则递归访问之
}

/*---------- 邻接表方式存储图 ----------*/

/* 前面都是准备工作, 下面才是重点 --> Prim 算法 */

Vertex FindMinDist(MGraph Graph, WeightType dist[]); // 先声明一下然后 Prim 算法才能用

/**
 * 将最小生成树保存为邻接表存储的图 MST, 返回最小权重和
 * @param Graph
 * @param MST 即 Minimun-cost Spanning Tree 最下生成树
 * @return
 */
int Prim(MGraph Graph, LGraph * MST)
{
    WeightType dist[MaxVertexNum], TotalWeight;
    Vertex parent[MaxVertexNum], V, W;
    int VCount;
    Edge E;

    // 初始化. 默认初始点下标是 0
    for (V = 0; V Nv; V++)
    {
        // 这里假设若 V 到 W 没有直接的边, 则 Graph->G[V][W] 定义为 INFINITY
        dist[V] = Graph->G[0][V]; // 初始时 dist 数组中的值设置为顶点 0 与 其它顶点之间的边的权重
        parent[V] = 0; // 暂且定义所有顶点的父节点都是初始点 0
    }
    TotalWeight = 0; // 初始化权重和
    VCount = 0; // 初始化收录的顶点数
    // 创建包含所有顶点但没有边的图. 注意用邻接表版本
    *MST = CreateLGraph(Graph->Nv);
    E = (Edge)malloc(sizeof(struct ENode)); // 建立空的边节点

    // 将初始点 0 收录进 MST
    dist[0] = 0;
    VCount++;
    parent[0] = -1; // 当前树根是 0

    while (1)
    {
        V = FindMinDist(Graph, dist);
        // 未被收录顶点中 dist 最小者
        if (V == ERROR) // 若这样的 V 不存在
            break;

        // 将 V 及相应的边  收录进 MST
        E->V1 = parent[V];
        E->V2 = V;
        E->Weight = dist[V];
        InsertLEdge(*MST, E);
        TotalWeight += dist[V];
        dist[V] = 0;
        VCount++;


        for (W = 0; W Nv; W++) // 对图中的每个节点
        {
            if (dist[W] != 0 && Graph->G[V][W] G[V][W] G[V][W]; // 更新 dist[W]
                    parent[W] = V; // 更新树
                }
            }
        }
    } // while 结束

    /* 测试 */
    // PrintLGraph(*MST);
    /* 测试 */

    if (VCount Nv) // MST 中收录的顶点不到 |V| 个
        TotalWeight = ERROR;
    return TotalWeight; // 算法执行完毕, 返回最小权重或错误标记
}

/**
 * 返回未被收录顶点中 dist 最小者
 * @param Graph
 * @param dist
 * @return
 */
Vertex FindMinDist(MGraph Graph, WeightType dist[])
{
    Vertex MinV, V; // Min 表示 dist 中的最小者, V 是临时变量
    WeightType MinDist = INFINITY; // 用来存储顶点 dist 最小的值

    for (V = 0; V Nv; V++)
    {
        if (dist[V] != 0 && dist[V] 

输出结果:

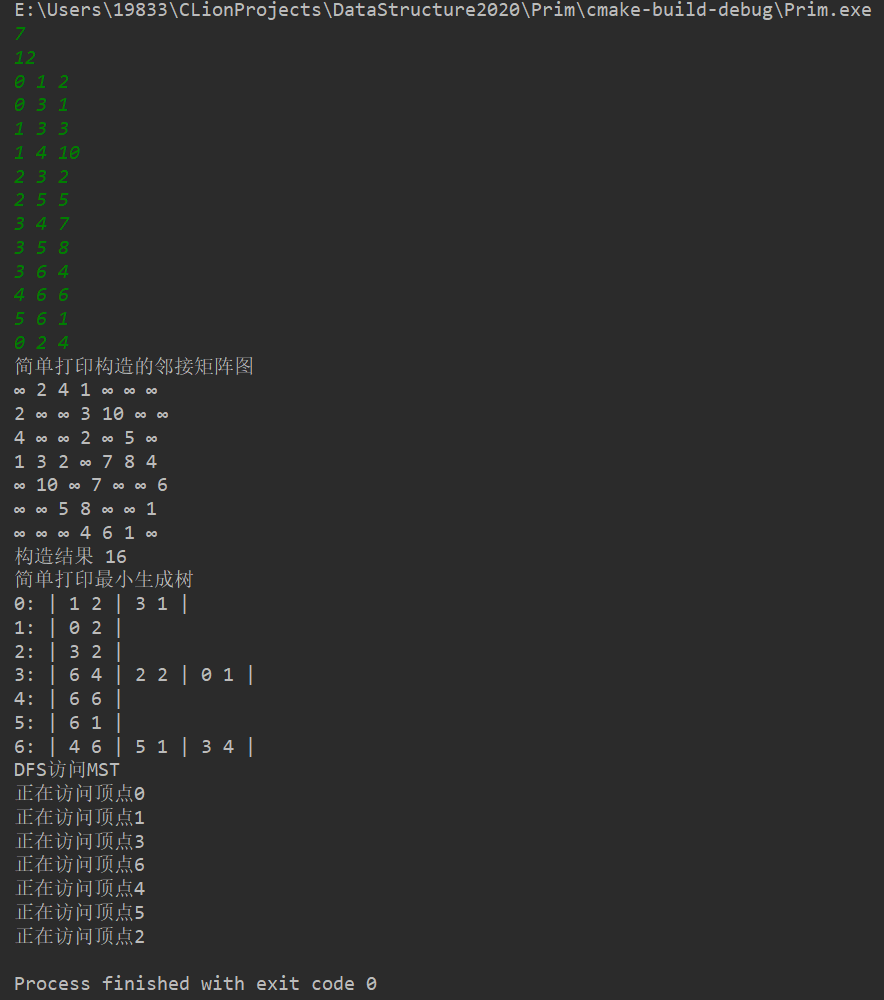
按 1 : 测试数据附在了上面的 main 函数的最后. 且测试所用数据与本文开头的两幅图保持一致.

按 2 : 由于上面的代码基本上是直接复用之前的图的邻接矩阵实现和图的邻接表实现的, 故, 上面的 BFS 代码中还需要用到另外一种数据结构 -- 队列. 代码如下:

queue.h

#ifndef PRIM_QUEUE_H
#define PRIM_QUEUE_H
#include 
typedef int ElementType;
typedef int Position;
typedef struct QNode * PtrToQNode;
struct QNode {
    ElementType * Data; // 存储元素的数组
    Position Front, Rear; // 队列的、尾指针
    int MaxSize; // 队列的最大容量
};
typedef PtrToQNode Queue;

Queue CreateQueue(int MaxSize);
bool IsFull(Queue Q);
bool AddQ(Queue Q, ElementType X);
bool IsEmpty(Queue Q);
ElementType DeleteQ(Queue);

#endif //PRIM_QUEUE_H

queue.c

#include "queue.h"
#include 
#include 

#define ERROR -1

Queue CreateQueue(int MaxSize)
{
    Queue  Q = (Queue)malloc(sizeof(struct QNode));
    Q->Data = (ElementType *)malloc(MaxSize * sizeof(ElementType));
    Q->Front = Q->Rear = 0;
    Q->MaxSize = MaxSize;
    return Q;
}

bool IsFull(Queue Q)
{
    return ((Q->Rear + 1) % Q->MaxSize == Q->Front); // 这里我们选择少用一个空间, 当队列尾指针加 1 就会从后面赶上头指针时 --> 队满
}

bool AddQ(Queue Q, ElementType X)
{
    if (IsFull(Q)) {
        printf("队列满");
        return false;
    } else {
        Q->Rear = (Q->Rear + 1) % Q->MaxSize; // 尾指针向后移动一个位置
        Q->Data[Q->Rear] = X;
        return true;
    }
}

bool IsEmpty(Queue Q)
{
    return (Q->Front == Q->Rear); // 头指针和尾指针相等时, 队列为空, 注意与队列满的时候作区分
}

ElementType DeleteQ(Queue Q)
{
    if (IsEmpty(Q)) {
        printf("队列空");
        return ERROR;
    } else {
        Q->Front = (Q->Front + 1) % Q->MaxSize;
        return Q->Data[Q->Front]; // 虽然这里 Q->Front 位置上的数据还在, 但是其实它已经被删除了, 因为我们是选择的少用一个空间
    }
}

按 3 : 这里的队列代码也是基本复用陈越老师教材中的代码.

按 4 : 千万要注意, 这里的图用的是无向图, 在复用之前有向图的时候, 我没有注意, 导致找了很长时间的 Bug!!

Prim 算法(浙江大学数据结构 陈越老师) 完整实现(含测试)

标签：else   相等   测试   包含   lan   版本   有向图   父节点   无向图   

原文地址：https://www.cnblogs.com/fanlumaster/p/14033105.html