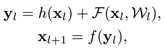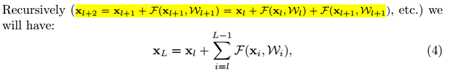经典网络结构(六)ResNet
2021-03-17 01:25
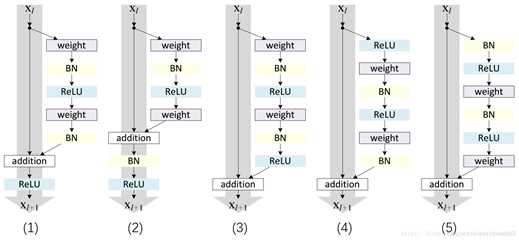
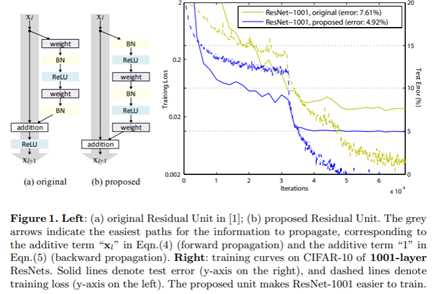
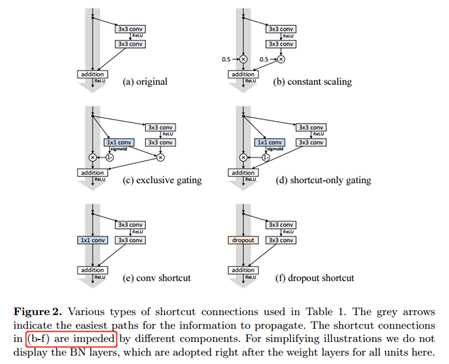
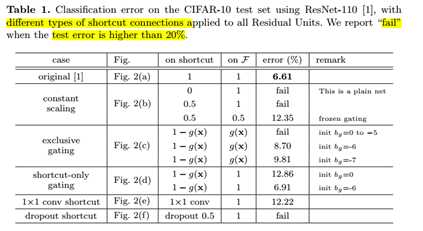
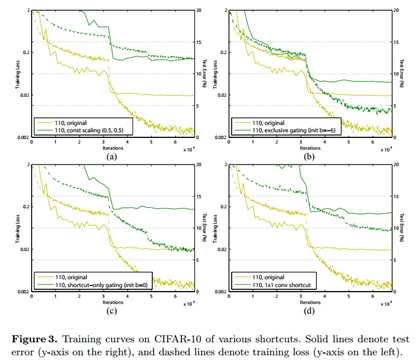
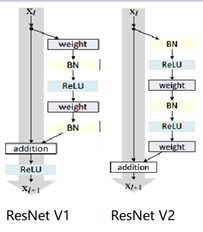
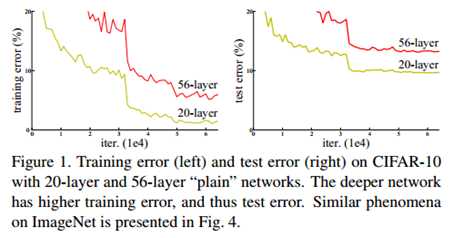
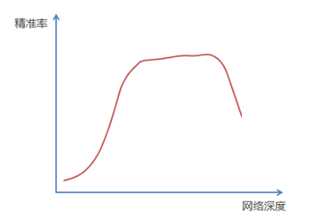
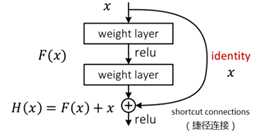
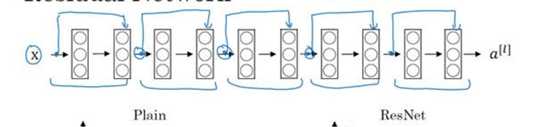
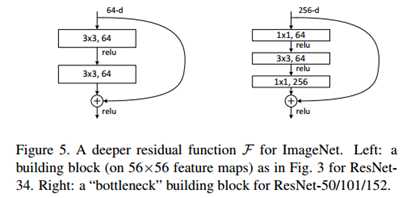
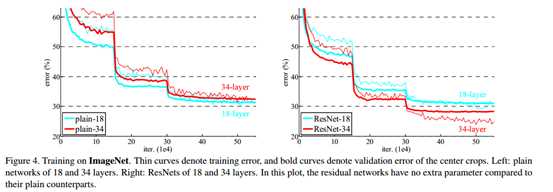
标签:bat 网络层 asi ping c函数 获得 改变 引入 实验 论文题目:Deep Residual Learning for Image Recognition 文献地址:https://arxiv.org/pdf/1512.03385.pdf 源码地址:https://github.com/KaimingHe/deep-residual-networks 论文题目:Identity Mappings in Deep Residual Networks 文献地址:https://arxiv.org/pdf/1603.05027.pdf 源码地址:https://github.com/KaimingHe/resnet-1k-layers ResNet v1: DBL结构 ResNet v2: post-activation or pre-activation BLD的结构, 先使用BN进行预激活。 深度学习最显著的特点就是它的网络深。之前在卷积神经网络中也提到过,浅层的卷积层只能提取一些诸如纹理等比较简单,抽象的特征,而比较深层的卷积层可以提取到诸如器官、人脸等比较复杂、具体的特征。 直观的感受:深的网络一般会比浅的网络好,想要提升模型的准确率,最直接的方法就是加深模型网络的深度。 然而,从之前介绍的经典深度网络(LeNet, AlexNet, VGG, GooLeNet)中可以看出,虽然网络深度有所增加,并且越深的效果越好,但总体网络层数并不大。如下图所示,最深的GooLeNet不过也就22层。为什么不直接搞个成百上千层呢? 对于一个常规网络,如下图所示,通过实验验证可得,当网络层数比较深的时候,模型的效果却越来越差(模型的误差越来越高)。如果对于神经网络有一定基础的话,其实不难理解,随着网络层数的加深,反向传播的过程中,靠后的网络参数可以获得比较好的训练更新,而比较靠前的网络,由于链式求导法则连乘的性质,梯度信号越来越弱,网络参数更新越来越难。 也就是说,随着网络的加深,网络将会遇到梯度弥散(梯度消失)的问题,深度网络变得难以训练,不同深度的层训练不同步。【举一个直观的例子,假如采用Sigmoid函数,对于幅度为1的信号,每向后传递一层,梯度就衰减为原来的0.25,层数越多,衰减越厉害】。 前面的实验描述的是,当网络比较深时,模型的准确率会不如浅层的神经网络。下面的实验描述的是随着网络层数的增加,模型的准确率会先上升,然后达到饱和,如果网络深度继续加深时,会导致准确率的下降,如下图所示: ResNet引入了残差网络结构(residual network),通过这种残差网络结构,可以把网络层弄的很深(据说目前可以达到1000多层),并且最终的分类效果也非常好,残差网络的基本结构如下图所示,很明显,该图是带有跳跃结构的: 从上述结构中可以看出,Residual network中包含一条捷径,可以直接将前两层的信息x传输到后两层,(其结构会想到过控当中的前馈控制)这种结构实际上是想让x无损失的传递到更深层的网络当中,也就是说,让模型自己去选择接受x的量。当第二层的权重和偏执为0时,就相当于只走了捷径,即a[l]直接将信息传到了a[l+2]。但如果仅这样理解,会感觉有种深层的网络好像也只是浅层的网络的错觉,你给它开辟了捷径,走捷径就好了。 实际上,这样种理解只是为了描述残差块具有学习恒等式函数的能力,也是证明当信息经过很深的层进行转换后,信息不会丢失。这是基于前向信息转换过程的理解。基于反向误差的传播过程的理解,其将深层的网络截成一小段、一小段的网络,并且能够保证误差在各段之间几乎无衰减的传播,而残差块中层数比较少,误差传播起来衰减的程度在可以接受的范围之内。这样也就有效的解决了深层网络中,梯度消失的问题。 深度学习中的问题不仅仅是随着网络层数的增加,误差的反向传播可能会消失弥散的问题,还有信息经过正向传播至网络输出时,信息也会有弥散丢失的问题。 【DenseNet】一文中有相应的描述: As CNNs become increasingly deep, a new research problem emerges: as information about the input or gradient passes through many layers, it can be vanish and "wash out" by the time it reaches the end (or begining) of the network. 从上述34层的结构图中可以看出,在网络的捷径中,有实线的捷径,也有虚线的捷径。 残差块有两层残差学习单元,也有三层残差学习单元,如下图所示yolo中用的就是三层的残差学习块。 三层的残差学习单元的结构与优化的Inception V1中的思想一致,首先由于输入的feature map的通道数量可能比较大,直接进行3*3卷积可能会造成卷积核参数数量过大。需要首先降低输入的feature map的通道数量,再进行3*3的same卷积,最后,为了与捷径进行很好的加和,需要采用1*1卷积将通道数量提升至256。 由于做的都是same卷积,但为了减少输入的尺寸,网络中会不定期的选择池化操作,或者步长为大于1的卷积操作 进行降采样。 以下是实验对比,可以看出加了残差块的深层网络能够获得更好的效果。 ResNet v2 和 ResNet v1 的主要区别在于, 以下有5张与Residual Network很像的图,一起来辨别真伪吧! 其中,weight为conv层; addition表示相加。 根据之前Residual Network v1的描述,仿佛这5种结构都能够满足要求。 那么2016年ResNet原文是哪一个结构呢?而且其他四组结构的设计是否可行? 首先, 2016年ResNet原文中使用的是结构(1),其特点包括: 【如果将右侧的部分称为residual分支,左侧的部分称为identity分支。】 按照常规,把两个DBL都放在residual分支中不更好么?就是(3)中的结构。那么(3)是否OK? 在(3)中,ReLU作为residual分支的结束,则residual分支得到的结果永远非负,这样前向的时候输入会单调递增,从而影响特征的表达能力。也就是说,希望residual分支的结果是(-∞, +∞)的。图(3)不OK!图(3)会使得前向过程输出单调递增,影响模型对于特征的表达。 那如果把BN和ReLU均移到addition后面呢?图(2)是否OK? 将BN也放在addition外面,BN将会改变identity分支的分布,影响了整个的信息传递,在训练的时候会阻碍loss的下降。 ----- 它的存在会有损反向传播过程中identity误差的传播。(它是一层,会对其进行链式法则的求导,会有衰减,会对后续的identity分支产生影响。层数多了,依旧会有梯度消失的可能) 因此,图(2)不OK! 图(2)会阻碍反向传播时梯度信息无障碍的传递。 综上ResNet的特点: 总之,就是让identity在反向的过程中,梯度信息可以无障碍的传递。 再来看图(1)~图(3)与图(4)~图(5)的区别,图(1)~图(3)是典型的"post-activation",而图(4)~图(5)是"pre-activation"。也就是激活函数是在conv层之前,还是之后。 【"post-activation"】 xl表示第l个残差单元的输入特征,Wl表示 作者将ResNet v1中相同形状连接堆叠的模块称之为残差单元(Residual Units)。 那实际上,残差网络可以表示为一个递归的运算: 也就是说,任意深层L的单元xL都可以表示成所有的残差输出的总和再加上x0。 对于Eq.4 其反向传播的可以表示为: Eq.5中,描述了在ResNet中,梯度可以分解为两个部分: 作者又分析了,如果在identity分支中增加一些东西的话(如下图的(b-f)),都会影响误差的反向传递。即使是一个因子λ,都会因反向传播时λ的连乘而导致误差信号的衰减。 Table 1 显示的实验结果验证了 short-cut中的操作 (缩放、门控、1×1 的卷积以及 dropout) 会阻碍误差信息的传递,以致于对优化造成困难。【门控与LSTM中的门一样,就是一个logistic函数】 接下来,才是关于ResNet V2的描述: 使用了He2016中的ResNet-110和164层瓶颈结构进行实验,残差单元包含一个1×1的层来降维,一个3×3的层,还有一个1×1的层来恢复维度。【之前提到的3层残差结构】 其在original的基础上,提出了4种变体,并论证其可能性:(前文详细的介绍过了) 从Table 2的实验结果上,我们可以发现图(4)的结构与ResNet原结构伯仲之间,稍稍逊色,然而图(5)的结构却好于ResNet原结构。 图5的结构好的原因在于两点: 1)反向传播基本符合假设,信息传递无阻碍; 2)BN层作为pre-activation,起到了正则化的作用; 经典网络结构(六)ResNet 标签:bat 网络层 asi ping c函数 获得 改变 引入 实验 原文地址:https://www.cnblogs.com/monologuesmw/p/13041632.html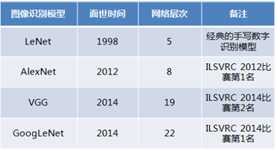
Residual Network v1


Residual Network v2