R语言-岭回归及lasso算法
2021-03-20 12:26
标签:lam let rgb complete min code gauss edit family 前文我们讲到线性回归建模会有共线性的问题,岭回归和lasso算法都能一定程度上消除共线性问题。 岭回归 我们可以看到这次模型的收入和支出是正相关了。 lasso算法 看模型数据,我们得知并没有解决income为负相关的情况,而且并没有筛选变量,那么我们尝试取lambda.1se*0.5的值 看结果,可知把一些变量删去了,消除共线性的问题,接下来我们看看lambda.1se的值 这次结果只留了一个变量,由此可知当lambda越大,变量保留的越少,一般我们在误差最小和一倍标准差内选择合适的λ。 R语言-岭回归及lasso算法 标签:lam let rgb complete min code gauss edit family 原文地址:https://www.cnblogs.com/ye20190812/p/13925000.html> #########正则化方法消除共线性
> ###岭回归
> ###glmnet只能处理矩阵
> library(glmnet)
> library(mice)
> creditcard_expcreditcard_exp[complete.cases(creditcard_exp),]
> x)])
> y])
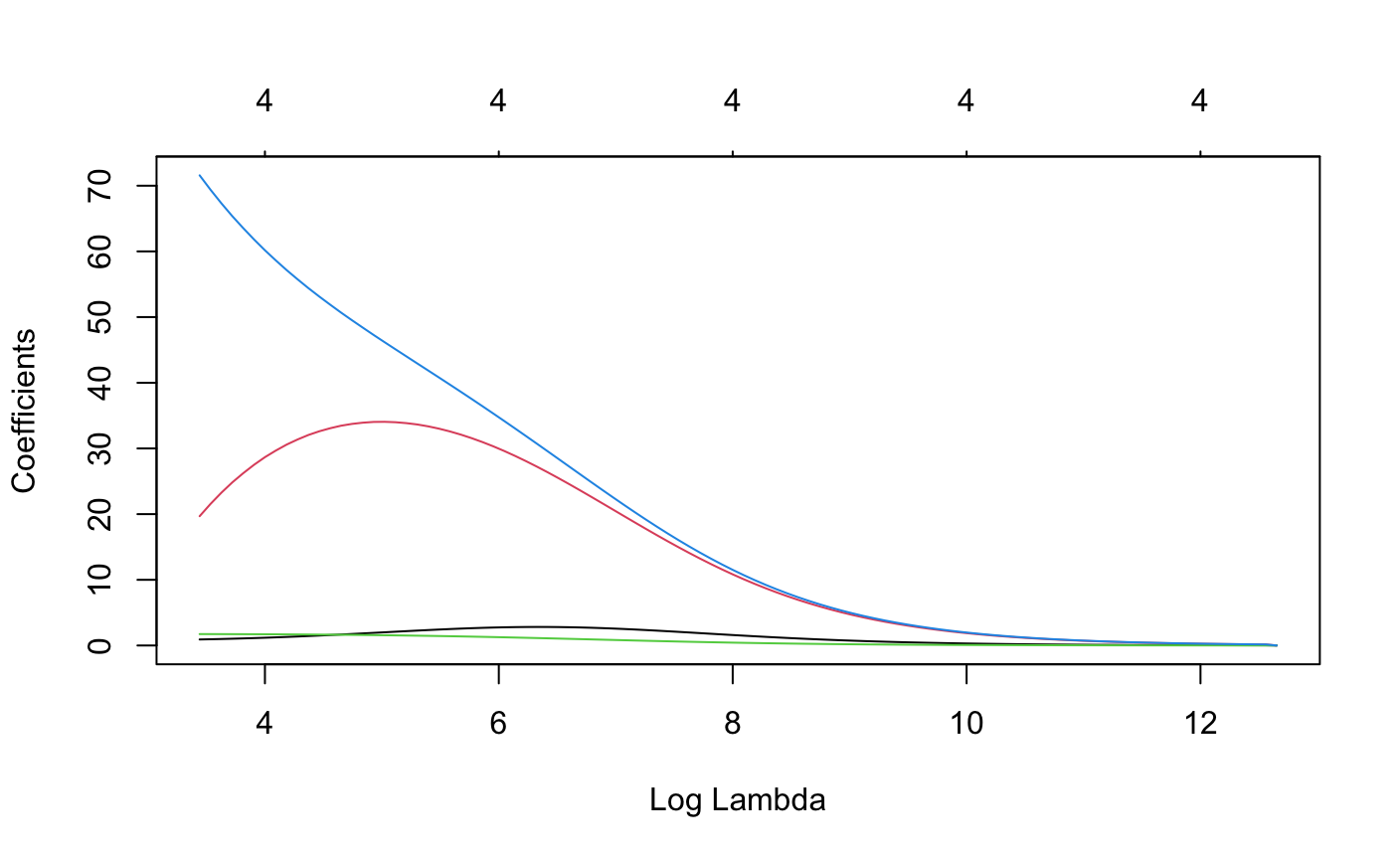
> #看一下岭脊图
> r1"gaussian",alpha = 0)#alpha = 0表示岭回归,x,y不能有缺失值
> plot(r1,xvar="lambda")
> r1cv"gaussian",alpha=0,nfolds = 10)#用交叉验证得到lambda
> plot(r1cv)
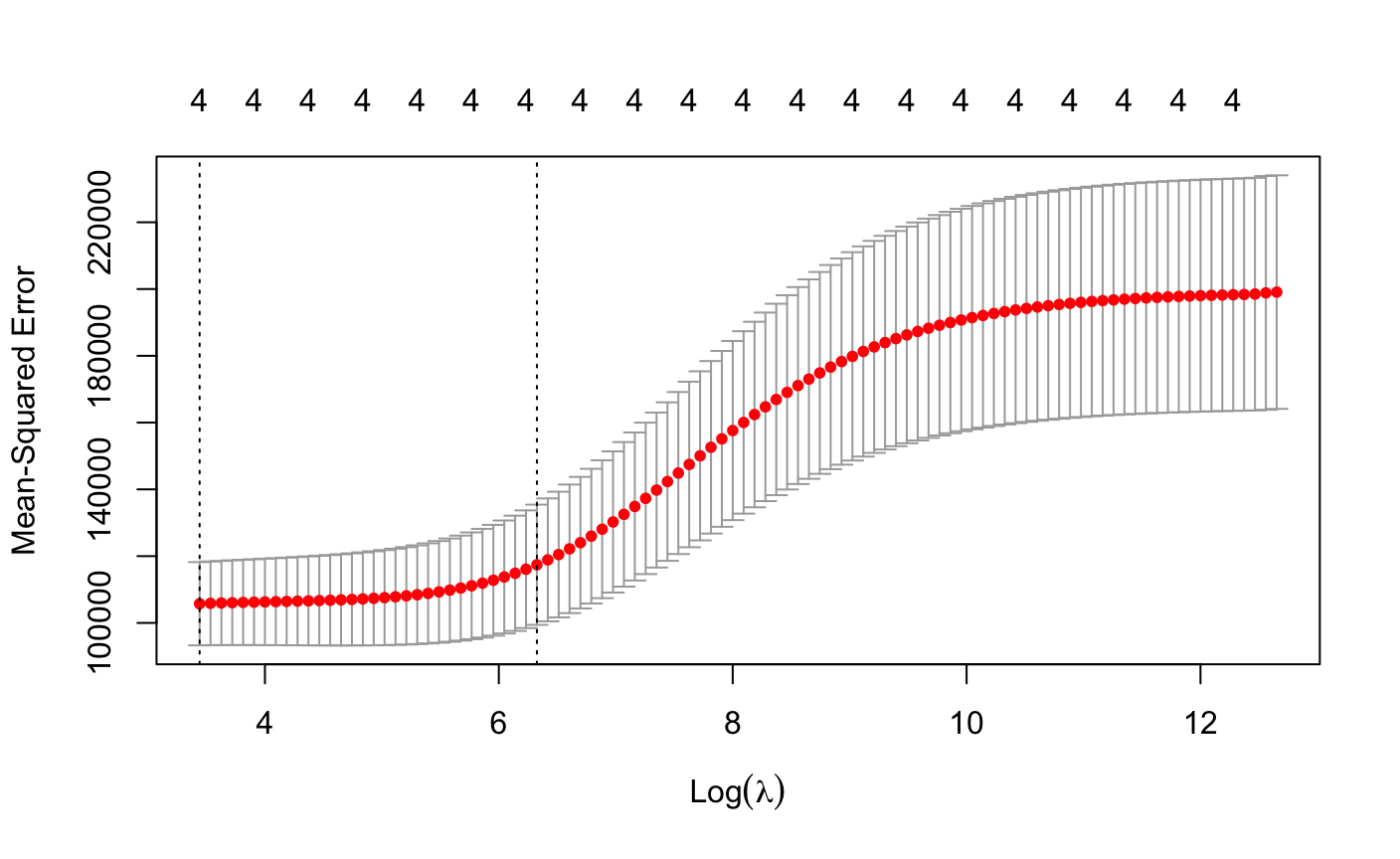
> rimin"gaussian",alpha = 0,lambda = r1cv$lambda.min)#取误差平方和最小时的λ
> coef(rimin)
5 x 1 sparse Matrix of class "dgCMatrix"
s0
(Intercept) 106.5467017
Age 0.9156047
Income 19.6903291
dist_home_val 1.7357213
dist_avg_income 71.5765458
#####Lasson算法:有变量筛选功效
r1l"gaussian",alpha=1,nfolds = 10)
plot(r1l)
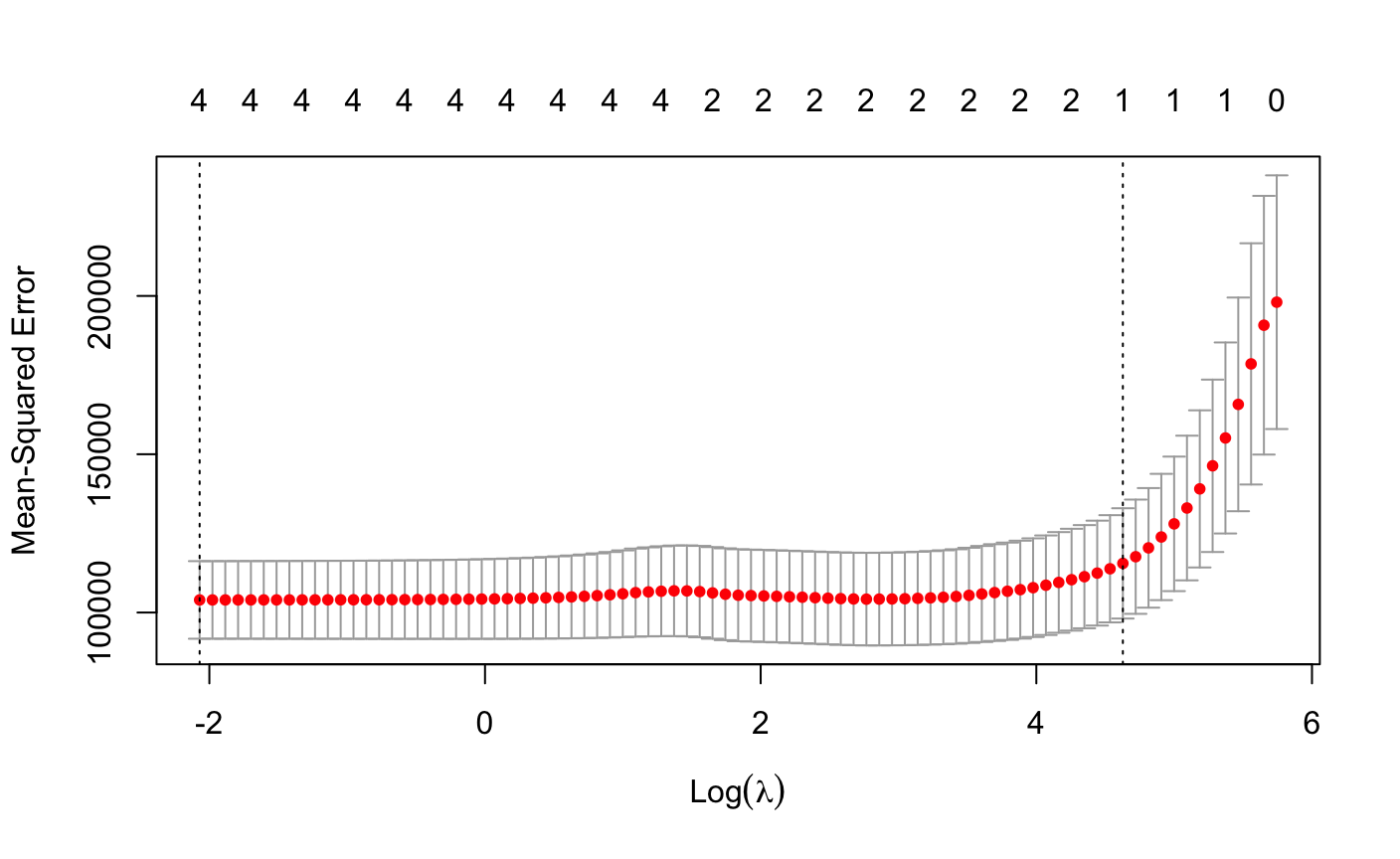
> r1l1"gaussian",alpha = 1,lambda = r1l$lambda.min)#取λ最小值看建模情况
> coef(r1l1)
5 x 1 sparse Matrix of class "dgCMatrix"
s0
(Intercept) -27.169039
Age 1.314711
Income -160.195837
dist_home_val 1.538823
dist_avg_income 255.395751
> r1l2"gaussian",alpha = 1,lambda = r1l$lambda.1se*0.5)#0.5倍标准误差的λ
> coef(r1l2)
5 x 1 sparse Matrix of class "dgCMatrix"
s0
(Intercept) 267.0510318
Age .
Income .
dist_home_val 0.6249539
dist_avg_income 83.6952253
1 > r1l3"gaussian",lambda = r1l$lambda.1se)
2 > coef(r1l3)
3 5 x 1 sparse Matrix of class "dgCMatrix"
4 s0
5 (Intercept) 432.00684
6 Age .
7 Income .
8 dist_home_val .
9 dist_avg_income 68.90894