反向传播算法
2021-03-30 00:27
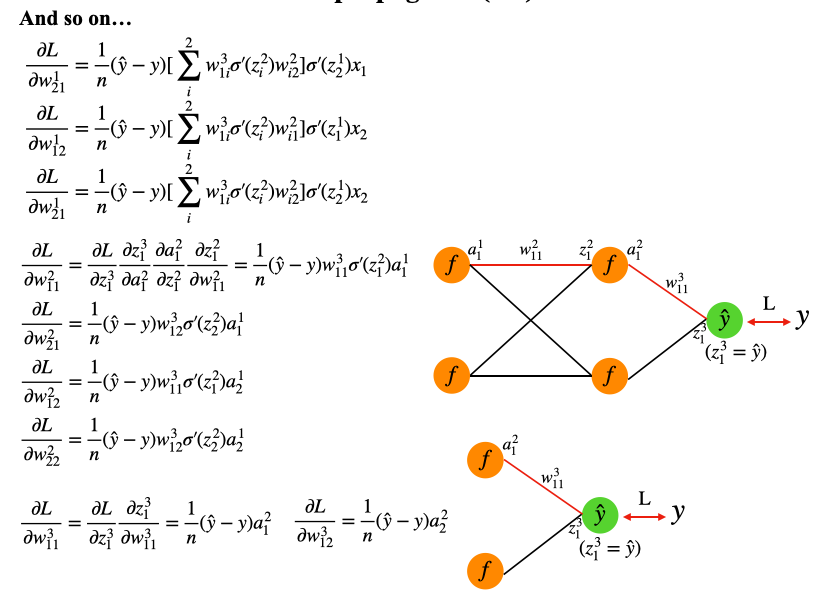
标签:通过 line math 一个 图片 网络图 sigma image 箭头 bp算法通过loss计算得到的误差,从最后的输出层,通过loss不断的向后,对能影响到loss变化的传播路径中各个隐藏层的神经元的输入和输出函数求偏导,更新目标权重的一个过程。 接下来我们看一下求BP的时候,需要的一些公式和知识点,loss我们使用mse代替,因为好算 我们以求解第1层第一个神经元的权重\(w_{11}^{1}\)为例子,红色箭头表示其会通过那些路径影响倒loss,反过来,loss也是通过原路径去影响到这个权重 对于其他层的权重,链式求导方式为 反向传播算法 标签:通过 line math 一个 图片 网络图 sigma image 箭头 原文地址:https://www.cnblogs.com/zhouyc/p/13589917.htmlBP公式推导
具体的计算方式如下。
先来构建一个网络图,然后我们定义一些数学符号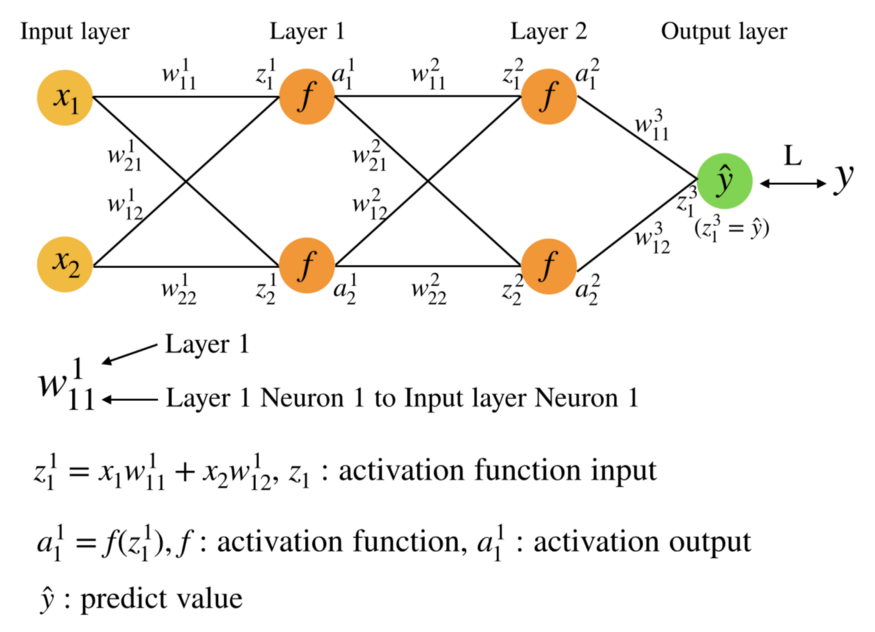
其中
其中需要注意的是,每一个神经元内部的结构有输入和输出,求偏导的时候,要分别考虑到它的输入和输出。如下所示: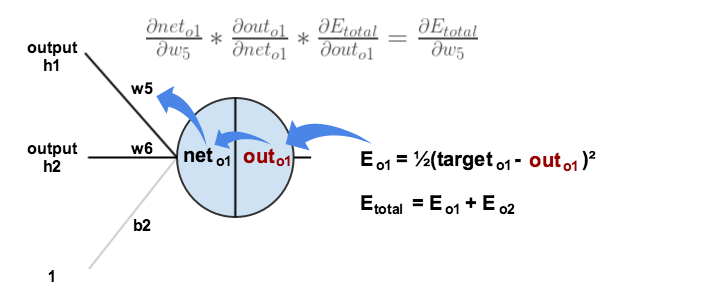

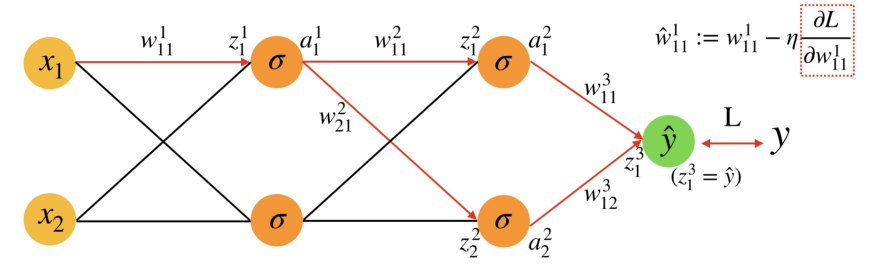
那么链式求导的公式为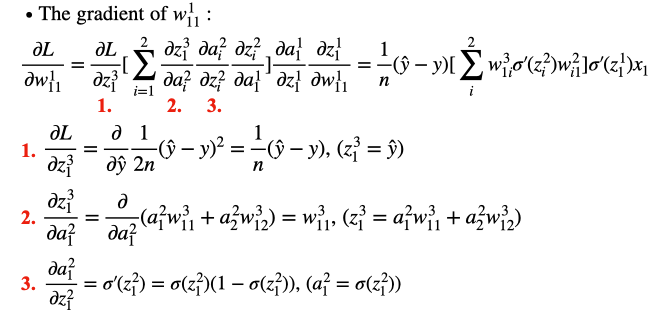
注意此处输出层并未被激活,所以我们忽略loss对输出的求导,否则loss还需要对\(\sigma(z)\) 求一次导