C#数据结构—图
2021-03-30 23:27
标签:1.2 个数 定义 连线 complete rect 因此 enc 大量 图状结构简称图,是另一种非线性结构,它比树形结构更复杂。树形结构中的结点是一对多的关系,结点间具有明显的层次和分支关系。每一层的结点可以和下一层的多个结点相关,但只能和上一层的一个结点相关。而图中的顶点(把图中的数据元素称为顶点)是多对多的关系,即顶点间的关系是任意的,图中任意两个顶点之间都可能相关。也就是说,图的顶点之间无明显的层次关系,这种关系在现实世界中大量存在。因此,图的应用相当广泛,在自然科学、社会科学和人文科学等许多领域都有着非常广泛的应用。 图(Graph)是由非空的顶点(Vertex)集合和描述顶点之间的关系——边(Edge)或弧(Arc)的集合组成。其形式化定义为: G=(V,E) V={v i |v i ∈某个数据元素集合} 其中,G 表示图,V 是顶点的集合,E 是边或弧的集合。在集合 E 中,P(vi,vj)表示顶点 vi 和顶点 vj 之间有边或弧相连。下图给出了图的示例。 在图 (a)中,V={v 1 ,v 2 ,v 3 ,v 4 ,v 5 }E={(v 1 ,v 2 ),(v 1 ,v 3 ),(v 2 ,v 4 ),(v 2 ,v 5 ),(v 3 ,v 4 ),(v 4 ,v 5 )} 在图 (b)中,V={v 1 ,v 2 ,v 3 ,v 4 ,v 5 }E={ 注:无向边用小括号“()”表示,而有向边用尖括号“”表示。 1、无向图:在一个图中,如果任意两个顶点v i 和v j 构成的偶对(v i ,v j )∈E是无序的,即顶点之间的连线没有方向,则该图称为无向图(Undirected Graph)。图 (a)是一个无向图。 2、有向图:在一个图中,如果任意两个顶点v i 和v j 构成的偶对 3、边、弧、弧头、弧尾:无向图中两个顶点之间的连线称为边(Edge),边用顶点的无序偶对(v i ,v j )表示,称顶点v i 和顶点v j 互为邻接点(Adjacency Point),(v i ,v j )边依附与顶点v i 和顶点v j 。有向图中两个顶点之间的连线称为弧(Arc),弧用顶点的有序偶对 4、无向完全图:在一个无向图中,如果任意两个顶点之间都有边相连,则称该图为无向完全图(Undirected Complete Graph)。可以证明,在一个含有 n 个顶点的无向完全图中,有 n(n-1)/2 条边。 5、有向完全图:在一个有向图中,如果任意两个顶点之间都存在方向互为相反的两条弧,则称该图为有向完全图(Directed Complete Graph)。可以证明,在一个含有 n 个顶点的有向完全图中,有 n(n-1)条弧。 6、顶点的度、入度、出度:在无向图中,顶点 v 的度(Degree)是指依附于顶点 v 的边数,通常记为 TD(v)。在有向图中,顶点的度等于顶点的入度(In Degree)与顶点的出度之和。顶点v的入度是指以该顶点v为弧头的弧的数目,记为ID(v);顶点 v 的出度(Out Degree)是指以该顶点 v 为弧尾的弧的数目,记为 OD(v)。所以,顶点 v 的度 TD(v)= ID(v)+ OD(v)。 例如,在无向图 (a)中有: TD(v 1 )=2 TD(v 2 )=3 TD(v 3 )=2 TD(v 4 )=3 TD(v 5 )=2 C#数据结构—图 标签:1.2 个数 定义 连线 complete rect 因此 enc 大量 原文地址:https://www.cnblogs.com/SimplePoint/p/9270805.html一:图
1.1:图的基本概念
1.1.1:图的定义
E={(v i ,v j )|v i ,v j ∈V∧P(v i ,v j )}或E={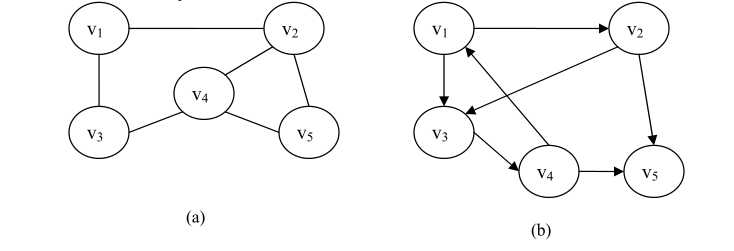
1.1.2:图的基本术语
在有向图 (b)中有:
ID(v 1 )=1 OD(v 1 )=2 TD(v 1 )=3
ID(v 2 )=1 OD(v 2 )=2 TD(v 2 )=3
ID(v 3 )=2 OD(v 3 )=1 TD(v 3 )=3
ID(v 4 )=1 OD(v 4 )=2 TD(v 4 )=3
ID(v 5 )=2 OD(v 5 )=0 TD(v 5 )=2