数据结构--二叉树(Java)
2021-04-06 10:28
标签:== block 常用 Fix 满二叉树 子节点 tor 最大 总结 博客说明 文章所涉及的资料来自互联网整理和个人总结,意在于个人学习和经验汇总,如有什么地方侵权,请联系本人删除,谢谢! 能提高数据存储,读取的效率, 比如利用 二叉排序树(Binary Sort Tree),既可以保证数据的检索速度,同时也可以保证数据的插入,删除,修改的速度 每个节点最多只能有两个子节点的一种形式称为二叉树 二叉树的子节点分为左节点和右节点 如果该二叉树的所有叶子节点都在最后一层,并且结点总数= 2^n -1 , n 为层数,则我们称为满二叉树。 如果该二叉树的所有叶子节点都在最后一层或者倒数第二层,而且最后一层的叶子节点在左边连续,倒数第二层的叶子节点在右边连续,我们称为完全二叉树 感谢 尚硅谷 万能的网络 以及勤劳的自己 关注公众号: 归子莫,获取更多的资料,还有更长的学习计划 数据结构--二叉树(Java) 标签:== block 常用 Fix 满二叉树 子节点 tor 最大 总结 原文地址:https://www.cnblogs.com/guizimo/p/13401192.html数据结构--二叉树(Java)
树的常用术语(结合示意图理解)
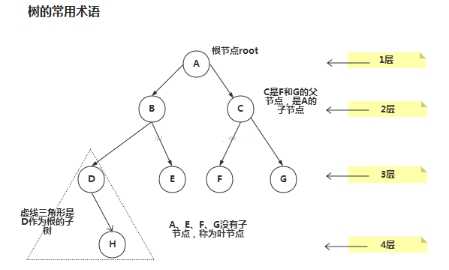
树存储方式优势
二叉树的概念
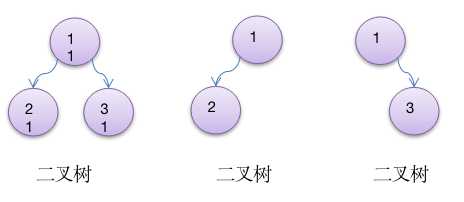
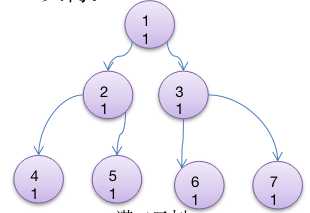
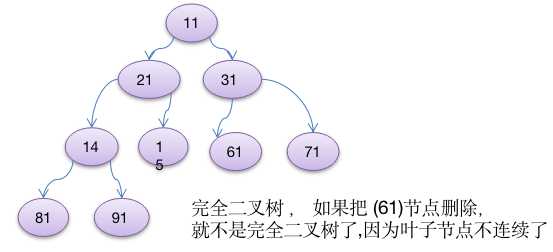
遍历
代码
package cn.guizimo.tree;
/**
* @author guizimo
* @date 2020/7/29 8:03 下午
*/
public class TreeDemo {
public static void main(String[] args) {
BinaryTree binaryTree = new BinaryTree();
HeroNode root = new HeroNode(1, "宋江");
HeroNode node2 = new HeroNode(2, "李逵");
HeroNode node3 = new HeroNode(3, "卢俊义");
HeroNode node4 = new HeroNode(4, "吴用");
HeroNode node5 = new HeroNode(5, "林冲");
HeroNode node6 = new HeroNode(6, "鲁智深");
//创建二叉树
root.setLeft(node2);
root.setRight(node3);
node2.setLeft(node4);
node3.setLeft(node5);
node3.setRight(node6);
binaryTree.setRoot(root);
//前序遍历
// HeroNode heroNode = binaryTree.preOrderSearch(5);
// System.out.println(heroNode);
}
}
/**
* 二叉树
*/
class BinaryTree {
//根节点
private HeroNode root;
public void setRoot(HeroNode root) {
this.root = root;
}
//删除二叉树的节点
public void delNode(int no) {
if (root != null) {
if (root.getNo() == no) {
root = null;
} else {
root.delNode(no);
}
} else {
System.out.println("二叉树为空");
}
}
//前序
public void preOrder() {
if (this.root != null) {
this.root.preOrder();
} else {
System.out.println("二叉树为空");
}
}
//中序
public void infixOrder() {
if (this.root != null) {
this.root.infixOrder();
} else {
System.out.println("二叉树为空");
}
}
//后序
public void postOrder() {
if (this.root != null) {
this.root.postOrder();
} else {
System.out.println("二叉树为空");
}
}
//前序查找
public HeroNode preOrderSearch(int no) {
if (root != null) {
return root.preOrderSearch(no);
} else {
return null;
}
}
//中序查找
public HeroNode infixOrderSearch(int no) {
if (root != null) {
return root.infixOrderSearch(no);
} else {
return null;
}
}
//后序查找
public HeroNode postOrderSearch(int no) {
if (root != null) {
return this.root.postOrderSearch(no);
} else {
return null;
}
}
}
/**
* 节点
*/
class HeroNode {
private int no;
private String name;
private HeroNode left;
private HeroNode right;
public HeroNode(int no, String name) {
this.no = no;
this.name = name;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public HeroNode getLeft() {
return left;
}
public void setLeft(HeroNode left) {
this.left = left;
}
public HeroNode getRight() {
return right;
}
public void setRight(HeroNode right) {
this.right = right;
}
@Override
public String toString() {
return "HeroNode{" +
"no=" + no +
", name=‘" + name + ‘\‘‘ +
‘}‘;
}
//删除节点
public void delNode(int no) {
//判读左节点是否为空,找到
if (this.left != null && this.left.no == no) {
this.left = null;
return;
}
//判断右节点,找到
if (this.right != null && this.right.no == no) {
this.right = null;
return;
}
//判断左节点,未找到,递归
if (this.left != null) {
this.left.delNode(no);
}
//判断右节点,未找到,递归
if (this.right != null) {
this.right.delNode(no);
}
}
//前序
public void preOrder() {
System.out.println(this);
if (this.left != null) {
this.left.preOrder();
}
if (this.right != null) {
this.right.preOrder();
}
}
//中序
public void infixOrder() {
if (this.left != null) {
this.left.infixOrder();
}
System.out.println(this);
if (this.right != null) {
this.right.infixOrder();
}
}
//后序
public void postOrder() {
if (this.left != null) {
this.left.postOrder();
}
if (this.right != null) {
this.right.postOrder();
}
System.out.println(this);
}
//前序遍历查找
public HeroNode preOrderSearch(int no) {
if (this.no == no) {
return this;
}
HeroNode resNode = null;
//判断左子树
if (this.left != null) {
resNode = this.left.preOrderSearch(no);
}
if (resNode != null) {
return resNode;
}
//判断右子树
if (this.right != null) {
resNode = this.right.preOrderSearch(no);
}
return resNode;
}
//中序遍历查找
public HeroNode infixOrderSearch(int no) {
HeroNode resNode = null;
if (this.left != null) {
resNode = this.left.infixOrderSearch(no);
}
if (resNode != null) {
return resNode;
}
if (this.no == no) {
return this;
}
if (this.right != null) {
resNode = this.right.infixOrderSearch(no);
}
return resNode;
}
//后序遍历查找
public HeroNode postOrderSearch(int no) {
HeroNode resNode = null;
if (this.left != null) {
resNode = this.left.postOrderSearch(no);
}
if (resNode != null) {
return resNode;
}
if (this.right != null) {
resNode = this.right.postOrderSearch(no);
}
if (resNode != null) {
return resNode;
}
if (this.no == no) {
return this;
}
return resNode;
}
}