数据结构与算法(23)——表达式解析
2021-04-08 10:27
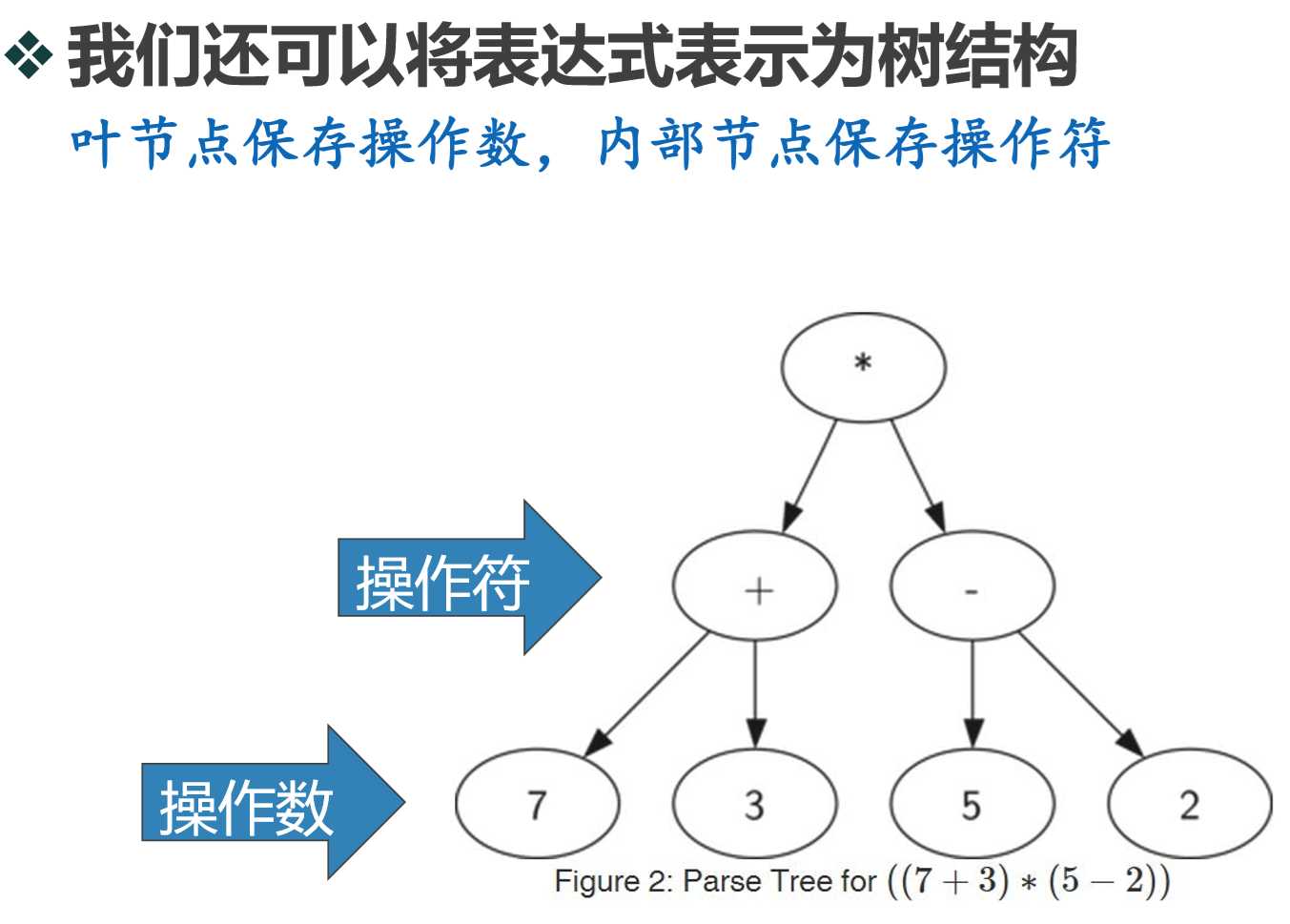
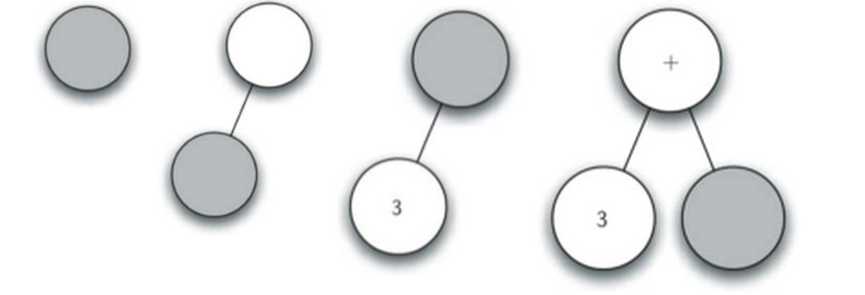
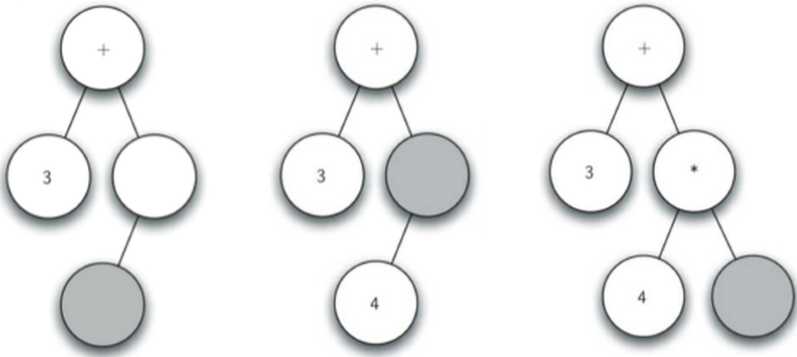
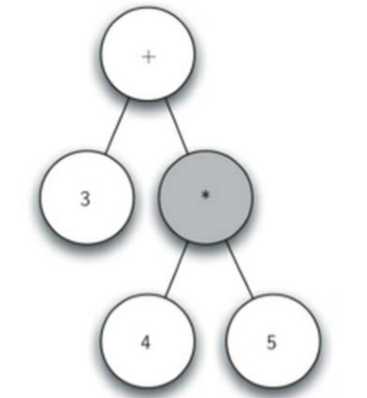
标签:font imp from 递归算法 return pstack int 左右 设置 解析全括号表达式:(3+(4*5)) 创建空树,当前节点为根节点 读入‘(‘,创建了左子节点,当前节点下降 读入‘3‘,当前节点设置为3,上升到父节点 读入‘+‘,当前节点设置为+,创建右子节点,当前节点下降。 读入‘(‘,创建左子节点,当前节点下降 读入‘4‘,当前节点设置为4,上升到父节点 读入‘*‘,当前节点设置为*,创建右子节点,当 前节点下降 读入‘5‘,当前节点设置为5,上升到父节点 读入‘)‘,上升到父节点 读入‘)‘,再上升到父节点 总结下:如果当前单词是"(":为当前节点添加一个新节 点作为其左子节点,当前节点下降为这个新节点 如果当前单词是操作符"+,-,/,*":将当前节点 的值设为此符号,为当前节点添加一个新节点作 为其右子节点,当前节点下降为这个新节点 如果当前单词是操作数:将当前节点的值设为此 数,当前节点上升到父节点 如果当前单词是")":则当前节点上升到父节点。 创建左右子树可调用insertLeft/Right 当前节点设置值,可以调用setRootVal 下降到左右子树可调用getLeft/RightChild 创建一个栈来跟踪父节点:当前节点下降时,将下降前的节点push入栈 当前节点需要上升到父节点时,上升到pop出栈的节点即可! 创建了表达式解析树,可用来进行求值。由于二叉树BinaryTree是一个递归数据 结构,自然可以用递归算法来处理。由前述对子表达式的描述,可从树的底层子树开 始,逐步向上层求值,最终得到整个表达式的值。 求值函数evaluate的递归三要素: 基本结束条件:叶节点是最简单的子树,没有左 右子节点,其根节点的数据项即为子表达式树的值 缩小规模:将表达式树分为左子树、右子树,即为缩小规模 调用自身:分别调用evaluate计算左子树和右 子树的值,然后将左右子树的值依根节点的操作 符进行计算,从而得到表达式的值 这里引用函数引用包 operator。 数据结构与算法(23)——表达式解析 标签:font imp from 递归算法 return pstack int 左右 设置 原文地址:https://www.cnblogs.com/yeshengCqupt/p/13372910.html

from Stack import Stack
from Binary_Tree import BinaryTree
def buildParseTree(fpexp):
fplist = fpexp.split()
pStack = Stack()
eTree = BinaryTree(‘‘) #创建一个空树
pStack.push(eTree)
currentTree = eTree
for i in fplist:
if i == "(":
currentTree.insertLeft(‘‘)
pStack.push(currentTree) #将老的当前节点入栈下降
currentTree = currentTree.getLeftChild()
elif i not in [‘+‘, ‘-‘, ‘*‘, ‘/‘, ‘)‘]:
currentTree.setRootVal(int(i)) #设置当前节点的值,为操作数
parent = pStack.pop() #出栈上升
currentTree = parent #上升
elif i in [‘+‘, ‘-‘, ‘*‘, ‘/‘]:
currentTree.setRootVal(i) #将当前阶段设置成操作符
currentTree.insertRight(‘‘) #创建右子树
pStack.push(currentTree) #把老的当前节点push到栈中
currentTree = currentTree.getRightChild()
elif i == ")":
currentTree = pStack.pop()
else:
raise ValueError
return eTree
flist = buildParseTree(‘( 3 + ( 4 * 5 ) )‘)
from Stack import Stack
from Binary_Tree import BinaryTree
def buildParseTree(fpexp):
fplist = fpexp.split()
pStack = Stack()
eTree = BinaryTree(‘‘) #创建一个空树
pStack.push(eTree)
currentTree = eTree
for i in fplist:
if i == "(":
currentTree.insertLeft(‘‘)
pStack.push(currentTree) #将老的当前节点入栈下降
currentTree = currentTree.getLeftChild()
elif i not in [‘+‘, ‘-‘, ‘*‘, ‘/‘, ‘)‘]:
currentTree.setRootVal(int(i)) #设置当前节点的值,为操作数
parent = pStack.pop() #出栈上升
currentTree = parent #上升
elif i in [‘+‘, ‘-‘, ‘*‘, ‘/‘]:
currentTree.setRootVal(i) #将当前阶段设置成操作符
currentTree.insertRight(‘‘) #创建右子树
pStack.push(currentTree) #把老的当前节点push到栈中
currentTree = currentTree.getRightChild()
elif i == ")":
currentTree = pStack.pop()
else:
raise ValueError
return eTree
flist = buildParseTree(‘( 3 + ( 4 * 5 ) )‘)
文章标题:数据结构与算法(23)——表达式解析
文章链接:http://soscw.com/index.php/essay/72825.html