标签:基础 std mamicode print sig ant 其它 否则 ret
一、边双连通分量
边双连通分量
边双连通图:若一个无向图中的去掉任意一条边都不会改变此图的连通性,即不存在桥,则称作边双连通图。
边双连通分量:无向图中,删除任意边后仍然能连通的块。简记为“e-DCC”。(无向连通图的极大边双连通分量)
定理:一张无向连通图是“边双连通图”,当且仅当任意一条边都包含在至少一个简单环中。
性质:桥把整张图拆成了若干个 e-DCC,并且桥不在任意一个 e-DCC。
Tarjan算法求边双连通分量
求出所有的桥以后,把桥边删除,原图变成了多个连通块,则每个连通块就是一个边双连通分量。先用 Tarjan 算法标记处所有的桥边,再对整个无向图 DFS 一遍(遍历的过程中不访问桥边),划分出每个连通块。
模板题链接 参考代码如下:
#include#define int long long
using namespace std;
const int N=5e4+5,M=3e5+5;
int n,m,x,y,cnt=1,hd[N],to[M1],nxt[M1],dfn[N],low[N],num,c[N],dcc;
bool g[M1];
void add(int x,int y){
to[++cnt]=y,nxt[cnt]=hd[x],hd[x]=cnt;
}
void tarjan(int x,int fa){
dfn[x]=low[x]=++num;
for(int i=hd[x];i;i=nxt[i]){
int y=to[i];
if(!dfn[y]){
tarjan(y,i);
low[x]=min(low[x],low[y]);
if(low[y]>dfn[x]) g[i]=g[i^1]=1;
}
else if(i!=(fa^1)) low[x]=min(low[x],dfn[y]);
}
}
void dfs(int x){
c[x]=dcc;
for(int i=hd[x];i;i=nxt[i]){
int y=to[i];
if(c[y]||g[i]) continue;
dfs(y);
}
}
signed main(){
scanf("%lld%lld",&n,&m);
for(int i=1;i){
scanf("%lld%lld",&x,&y);
add(x,y),add(y,x);
}
for(int i=1;i)
if(!dfn[i]) tarjan(i,0);
for(int i=1;i)
if(!c[i]) ++dcc,dfs(i);
printf("%lld\n",dcc);
return 0;
}
dcc 为 e-DCC 的数量,c[x] 为节点 x 所属的“边双连通分量”的编号。
边双连通分量缩点
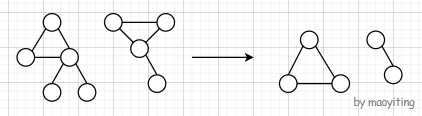
将所有的边双连通分量都缩成一个点,把边 (x,y) 看作连接编号 c[x] 和 c[y] 的边双连通分量对应结点的无向边,则原图会变成一棵树(若原来的无向图不连通,则产生森林)。
int cnt2=1,hd2[N],to2[N1],nxt2[N1];
void add2(int x,int y){
to2[++cnt2]=y,nxt2[cnt2]=hd2[x],hd2[x]=cnt2;
}
/*.......*/
int main(){
/*.......*/
for(int i=2;i){
int x=to[i^1],y=to[i];
if(c[x]!=c[y]) add2(c[x],c[y]);
}
//dcc 为缩点后森林的点数,cnt2/2 为缩点后森林的边数
for(int i=2;i2)
printf("%lld %lld\n",to2[i^1],to2[i]);
}
有桥图加边变成边双连通图
一个有桥的连通图,通过加边变成边双连通图:求出所有的桥以后,把桥边删除,原图变成了多个连通块,则每个连通块就是一个边双连通分量。把每个双连通分量都缩成一个点,得到一棵树。统计出树中度为 1 的结点的个数,即叶节点的个数,记为 leaf。则至少在树上添加 (leaf+1)/2 条边。
结论:当叶子数为 1 时,将一个有桥图通过加边变成边双连通图至少要添加的边数为0;否则为 (叶子数+1)/2。
[USACO06JAN]Redundant Paths G
要求任意两点间至少有两条没有公共边的路,也就是说所要求的图是一个边双连通图。总结为,给定一个图,求需要添加几条边使其变成边双连通图。根据上面提到的,将一个有桥图通过加边变成边双连通图,至少要加 (leaf+1)/2 条边。
#include#define int long long
using namespace std;
const int N=5e3+5,M=1e4+5;
int n,m,x,y,cnt=1,hd[N],to[M1],nxt[M1],dfn[N],low[N],num,dcc,c[N],du[N],leaf;
bool g[M1];
void add(int x,int y){
to[++cnt]=y,nxt[cnt]=hd[x],hd[x]=cnt;
}
void tarjan(int x,int fa){
dfn[x]=low[x]=++num;
for(int i=hd[x];i;i=nxt[i]){
int y=to[i];
if(!dfn[y]){
tarjan(y,i);
low[x]=min(low[x],low[y]);
if(low[y]>dfn[x]) g[i]=g[i^1]=1;
}
else if(i!=(fa^1)) low[x]=min(low[x],dfn[y]);
}
}
void dfs(int x){
c[x]=dcc;
for(int i=hd[x];i;i=nxt[i]){
int y=to[i];
if(c[y]||g[i]) continue;
dfs(y);
}
}
signed main(){
scanf("%lld%lld",&n,&m);
for(int i=1;i){
scanf("%lld%lld",&x,&y);
add(x,y),add(y,x);
}
for(int i=1;i)
if(!dfn[i]) tarjan(i,0);
for(int i=1;i)
if(!c[i]) ++dcc,dfs(i);
for(int i=2;i2){
int x=to[i^1],y=to[i];
if(c[x]!=c[y]) du[c[x]]++,du[c[y]]++;
}
for(int i=1;i)
if(du[i]==1) leaf++;
printf("%lld\n",(leaf+1)/2);
return 0;
}
二、点双连通分量
点双连通分量
点双连通:若一个无向图中的去掉任意一个节点都不会改变此图的连通性,即不存在割点,则称作点双连通图。
点双连通分量:无向图中,删除任意点后仍然能连通的块。简记为“v-DCC”。(无向图的极大点双连通子图)
定理:一张无向连通图是“点双连通图”,当且仅当满足下列两个条件之一:
- 图的顶点数不超过2
- 图中任意两点都同时包含在至少一个简单环中。(简单环:不自交的环)
性质:
- v-DCC 中没有割点。
- 若 v-DCC 间有公共点,则公共点为原图的割点。
- 对于图G,割点可能同时属于多个 v-DCC,其它点只可能属于一个 v-DCC。
- 割点将整张图分成若干个点 v-DCC。
Tarjan算法求点双连通分量
若某个节点为孤立点,则它自己单独构成一个 v-DCC。除了孤立点之外,点双连通分量的大小至少为 2。根据 v-DCC 定义中的“极大”性,虽然桥不属于任何 e-DCC,但是割点可能属于多个 v-DCC。
对于点双连通分量,实际上在求割点的过程中就能顺便求出每个点双连通分量。建立一个栈,存储当前双连通分量,在搜索图时,每找到一条树枝边或后向边(非横叉边),就把这条边加入栈中。如果遇到满足 dfn[x]≤low[y],说明 x 是一个割点,同时把边从栈顶一个个取出,直到遇到边 (x,y) 为止。取出的这些边与其相连的点,组成一个 v-DCC。对于两个 v-DCC,最多只有一个公共点即割点。
模板题链接 参考代码如下:
#include#define int long long
using namespace std;
const int N=5e4+5,M=3e5+5;
int n,m,x,y,cnt=1,hd[N],to[M1],nxt[M1],dfn[N],low[N],num,root,top,tot,st[N];
bool g[N];
vectorint>dcc[N];
void add(int x,int y){
to[++cnt]=y,nxt[cnt]=hd[x],hd[x]=cnt;
}
void tarjan(int x){
dfn[x]=low[x]=++num,st[++top]=x;
if(x==root&&!hd[x]) return (void)(dcc[++tot].push_back(x)); //孤立点
int flag=0;
for(int i=hd[x];i;i=nxt[i]){
int y=to[i];
if(!dfn[y]){
tarjan(y),low[x]=min(low[x],low[y]);
if(low[y]>=dfn[x]){
flag++;
if(x!=root||flag>1) g[x]=1;
dcc[++tot].push_back(st[top]);
while(st[top]!=y) dcc[tot].push_back(st[--top]);
--top,dcc[tot].push_back(x);
}
}
else low[x]=min(low[x],dfn[y]);
}
}
signed main(){
scanf("%lld%lld",&n,&m);
for(int i=1;i){
scanf("%lld%lld",&x,&y);
if(x==y) continue;
add(x,y),add(y,x);
}
for(int i=1;i)
if(!dfn[i]) root=i,tarjan(i);
for(int i=1;i)
for(int j=0;j)
printf("%lld%c",dcc[i][j],j==dcc[i].size()-1?‘\n‘:‘ ‘);
return 0;
}
在求出割点的同时,计算出 vector 数组 dcc,dcc[i] 保存编号为 i 的 v-DCC 中的所有节点。
点双连通分量缩点
因为一个割点可能属于多个 v-DCC,所以 v-DCC 的缩点比 e-DCC 要复杂一些。设图中共有 p 个割点和 t 个 v-DCC。我们建立一张包含 p+t 个节点的新图,把每个 v-DCC 和每个割点都作为新图中的节点,并在每个割点与包含它的所有 v-DCC 之间两边。容易发现,这张新图其实是一棵树(或森林)。
以下代码建立在 Tarjan 求个点和 v=DCC 的代码 main 函数的基础上,对 v-DCC 缩点,构成一棵新的树(或森林),存储在另一个邻接表中。
int cnt2=1,hd2[N],to2[N1],nxt2[N1];
void add2(int x,int y){
to2[++cnt2]=y,nxt2[cnt2]=hd2[x],hd2[x]=cnt2;
}
/*.......*/
int main(){
/*.......*/
//给每个割点一个新的编号(编号从 tot+1 开始)
num=tot;
for(int i=1;i)
if(g[i]) k[i]=++num;
//建新图,从每个 v-DCC 到它包含的所有割点连边
for(int i=1;i)
for(int j=0;j){
int x=dcc[i][j];
if(g[x]) add2(i,k[x]),add2(k[x],i);
else c[x]=i; //除割点外,其他点仅属于 1 个 v-DCC
}
//缩点之后的森林,点数为 num,边数为 cnt2/2
//编号 1~tot 的为原图的 v-DCC,编号 >tot 的为原图割点
for(int i=2;i2)
printf("%lld %lld\n",to2[i^1],to2[i]);
return 0;
}
Tarjan算法 双连通分量
标签:基础 std mamicode print sig ant 其它 否则 ret
原文地址:https://www.cnblogs.com/maoyiting/p/12674092.html
