AutoEncoder
2021-04-11 09:26
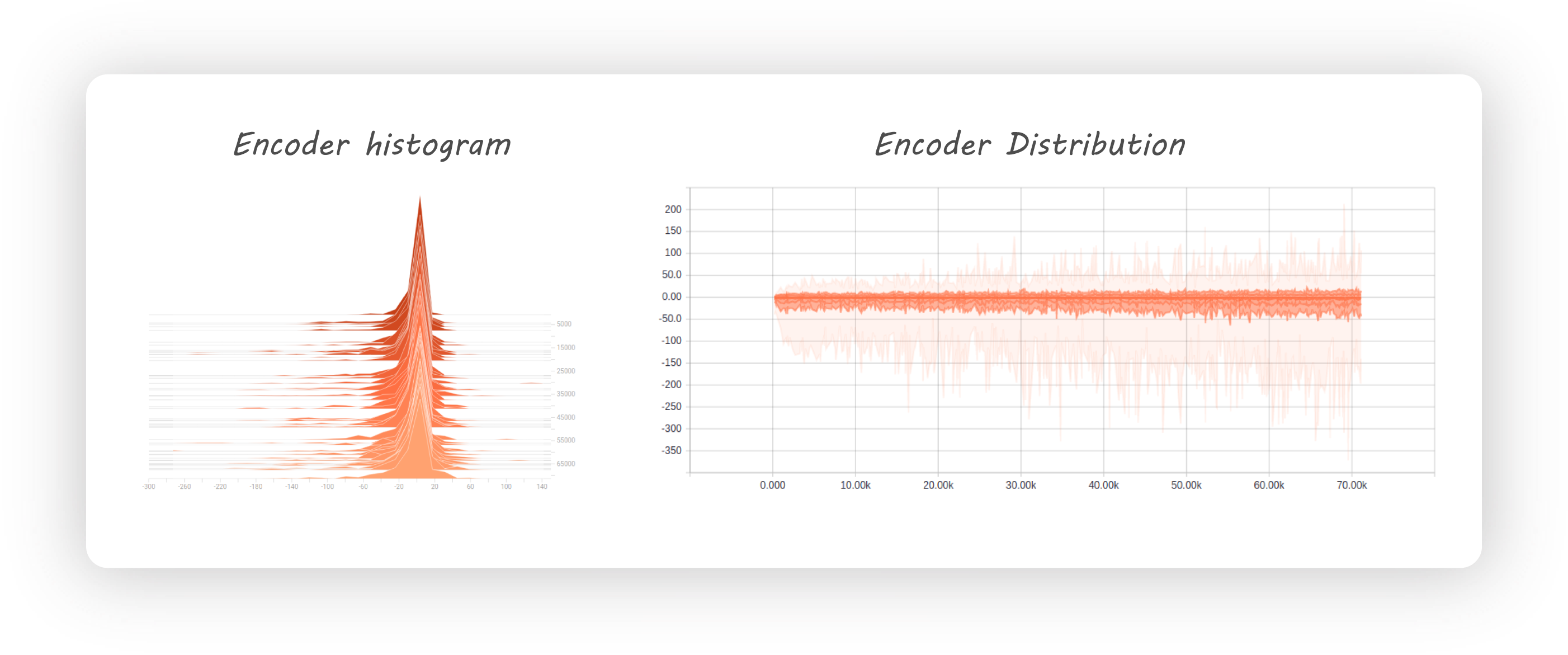
标签:属性 pen 等于 方法 使用 ram 现在 NPU 实验 自编码AutoEncoder是一种无监督学习的算法,他利用反向传播算法,让目标值等于输入值。什么意思呢,下面举个例子 有一个神经网络,它在做的事情是,输入一张图片,通过一个Encoder神经网络,输出一个比较"浓缩的"feature map。之后将这个feature map通过一个Decoder网络,结果又将这张图片还原回去了 你也可以这么理解,整个Encoder+Decoder是一个神经网络,中间的code只是暂存的数据 感觉就像是,现在有一锅红糖水,你不停的煮它,最终水都被煮干了,只剩下红糖,这个红糖就是上图的"Code"。然后你再向红糖里面注水、加热,结果又还原回了一锅红糖水 假设上面的神经网络展开如下图所示,可以看出,图片经过了一个压缩,再解压的工序。当压缩的时候,原有的图片质量被缩减。解压时,用信息量少却包含所有关键信息的文件恢复出了原本的图片。为什么要这样做呢? 因为有时候神经网络要接受大量的输入信息,比如说输入信息是高清图片时,信息量可能高达上千万,让神经网络直接从上千万个信息中进行学习是很吃力的。所以,为何不压缩一下,提取出原图片中最具代表性的信息,缩减输入信息量,再把缩减后的信息带入进行网络学习。这样学习起来就轻松多了 下图是一个AutoEncoder的三层模型,其中\(W^*=W^T\),\(W^*\)没有什么含义,仅仅是个变量名字而已,用来区分\(W\),你也可以管\(W^*\)叫\(W'\) Vincent在2010年的论文中做了研究,发现只要单组\(W\)就可以了,即\(W^*=W^T\)。\(W^*\)和\(W^T\)称为Tied Weights(绑定的权重),实验证明,\(W^*\)真的只是在打酱油,完全没有必要去训练 如果是实数作为输入,Loss function就是 同样都是降维,PCA和AutoEncoder谁的效果更好呢? 首先从直觉上分析,PCA本质上是线性的变换,所以它是有局限性的。而AutoEncoder是基于DNN的,由于有activation function的存在,所以可以进行非线性变换,使用范围更广 下图展示了MNIST数据集分别经过PCA和AutoEncoder降维再还原后的效果。第二行是是使用AutoEncoder的方法,可以看到几乎没什么太大变化;而第四行的图片很多都变得非常模糊了。说明PCA的效果是不如AutoEncoder的 Vincent在2008的论文中提出了AutoEncoder的改良版——dA,论文标题叫"Extracting and Composing Robust Features",译成中文就是"提取、编码出具有鲁棒性的特征" 首先我们考虑,为什么会产生这样的变种AutoEncoder。如果我们仅仅只是在像素级别对一张图片进行Encode,然后再重建,这样就无法发现更深层次的信息,很有可能会导致网络记住了一些特征。为了防止这种情况产生,我们可以给输入图片加一些噪声,比方说生成和图片同样大小的高斯分布的数据,然后和图像的像素值相加(见下图)。如果这样都能重建原来的图片,意味着这个网络能从这些混乱的信息中发现真正有用的特征,此时的Code才能代表输入图片的"精华" 关键是,这样胡乱给原始图片加噪声真的科学吗?Vincent从大脑认知角度给了解释。Paper中说到: 人类具有认识被阻挡的破损图像的能力,源于我们高等的联想记忆感受机能 就是说,我们能以多种形式去记忆(比如图像、声音),所以即便是数据破损丢失,我们也能回想起来 其实这个没什么特别的,平时我们不论是CNN还是RNN几乎都会用到Dropout。据说Dropout是当时Hilton在给学生上课的时候提到的,用来帮助提升神经网路训练效果的小Trick。具体关于Dropout的讲解可以看我的这篇文章 在AutoEncoder中可能存在这样一个问题,图片经过Encode之后的vector并不符合我们希望的分布(例如高斯分布),他的分布很有可能如下图所示。这其实是令我们不太满意的(虽然我并不知道Code满足分布到底有重要,但是既然别人认为很重要那就重要吧),那么有什么解决办法呢? 由University of Toronto、Google Brain和OpenAI合作的文章Adversarial Autoencoders(AAE)提出了一个使用Autoencoder进行对抗学习的idea,某种程度上对上述问题提供了一些新思路 AAE的核心其实就是利用GAN的思想,利用一个生成器G和一个判别器D进行对抗学习,以区分Real data和Fake data。具体思路是这样的,我现在需要一个满足\(p(z)\)概率分布的\(z\)向量,但是\(z\)实际上满足\(q(z)\)分布。那么我就首先生成一个满足\(p(z)\)分布的\(z'\)向量,打上Real data的标签,然后将\(z\)向量打上Fake data的标签,将它们俩送入判别器D。判别器D通过不断学习,预测输入input是来自于Real data(服从预定义的\(p(z)\)分布)还是Fake data(服从\(q(z)\)分布)。由于这里的\(p(z)\)可以是我们定义的任何一个概率分布,因此整个对抗学习的过程实际上可以认为是通过调整Encoder不断让其产生数据的概率分布\(q(z)\)接近我们预定义的\(p(z)\) 基本上AAE的原理就讲完了,还剩最后一个问题,AAE的Loss function是什么? 下面简述KL散度的公式推导。假设\(p\)和\(q\)均是服从\(N(\mu_1,\sigma^2_1)\)和\(N(\mu_2, \sigma_2^2)\)的随机变量的概率密度函数,则 前面的各种AutoEncoder都是将输入数据转换为vector,其中每个维度代表学习到的数据。而Variational AutoEncoders(VAE)提供了一种概率分布的描述形式,VAE中Encoder描述的是每个潜在属性的概率分布,而不是直接输出一个值 举例来说,假设我们已经在一个AutoEncoder上训练了一个6维的vector,这个6维的vector将学习面部的一些属性,例如肤色、是否戴眼镜等 在上面的示例中,我们使用单个值来描述输入图像的潜在属性。但是,我们可能更喜欢将每个潜在属性表示为一个范围。VAE就可以实现这个功能,如下图所示 通过这种方法,我们现在将给定输入的每个潜在属性表示为概率分布。从状态解码(Decode)时,我们将从每个潜在状态分布中随机采样以生成向量来作为解码器的输入 现在问题来了, 通过reparameterization,we can now optimize the parameters of the distribution, while still maintaing \(\varepsilon\)。就是说,我们保持\(\varepsilon\)不变,因为\(\varepsilon\)不需要学习修正,我们更新的只有\(\mu\)和\(\sigma\) AutoEncoder 标签:属性 pen 等于 方法 使用 ram 现在 NPU 实验 原文地址:https://www.cnblogs.com/mathor/p/12416575.html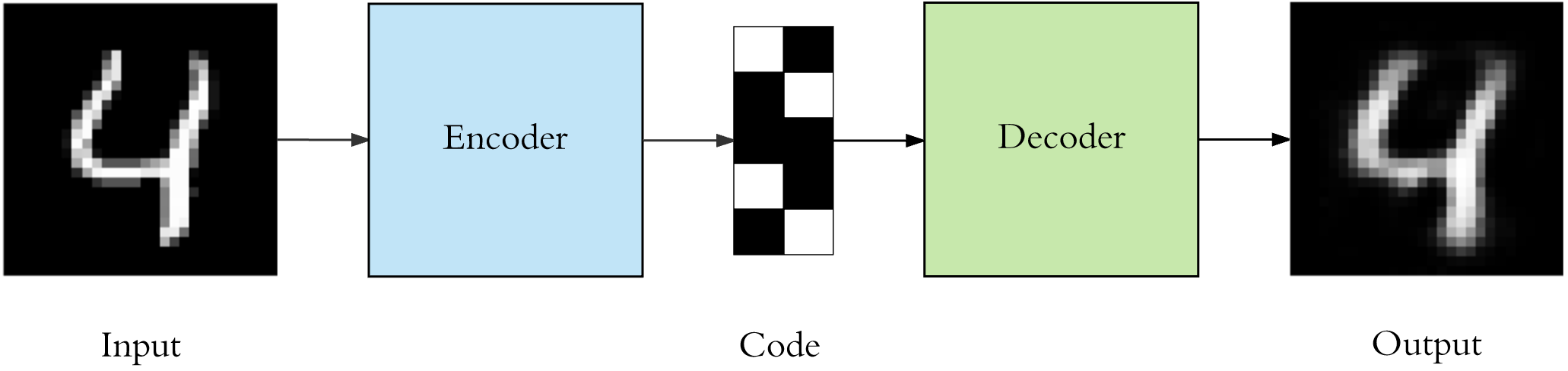
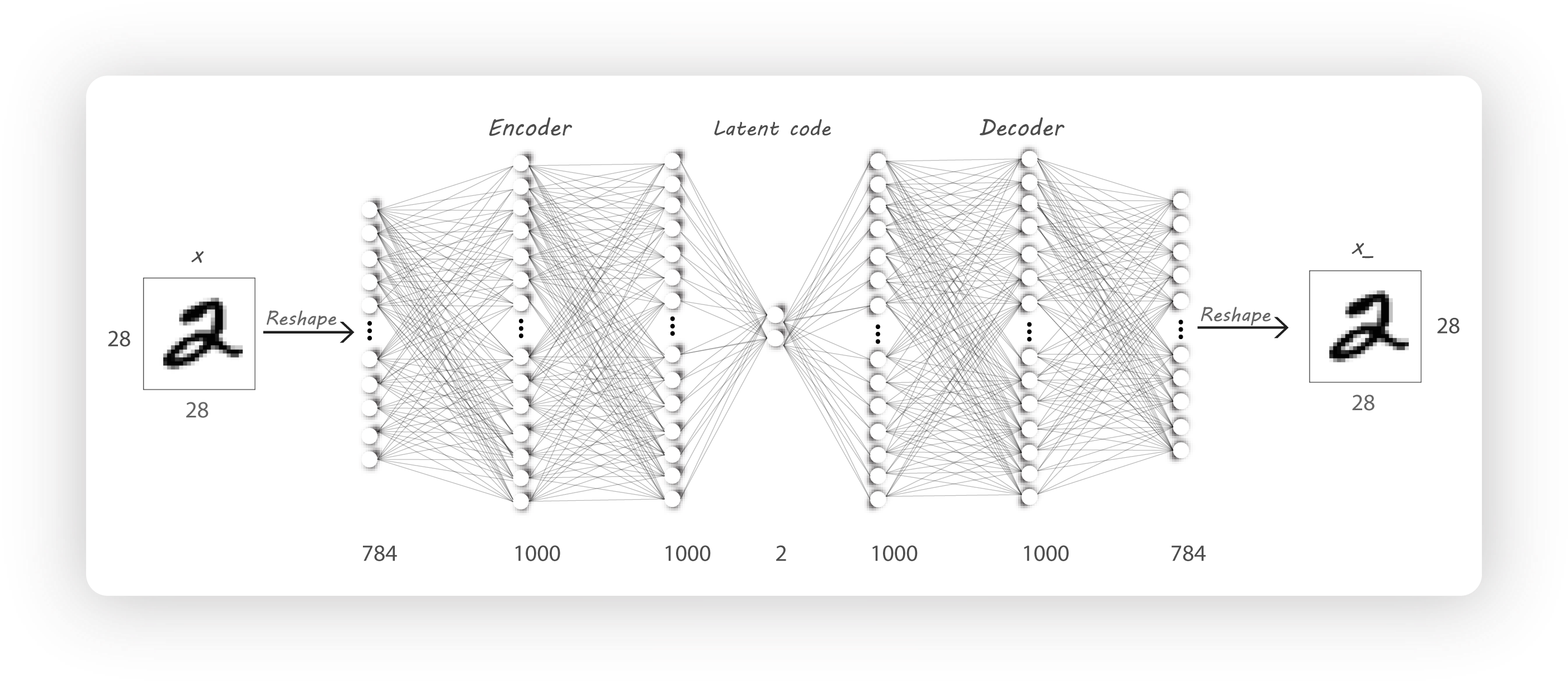
How to Train?
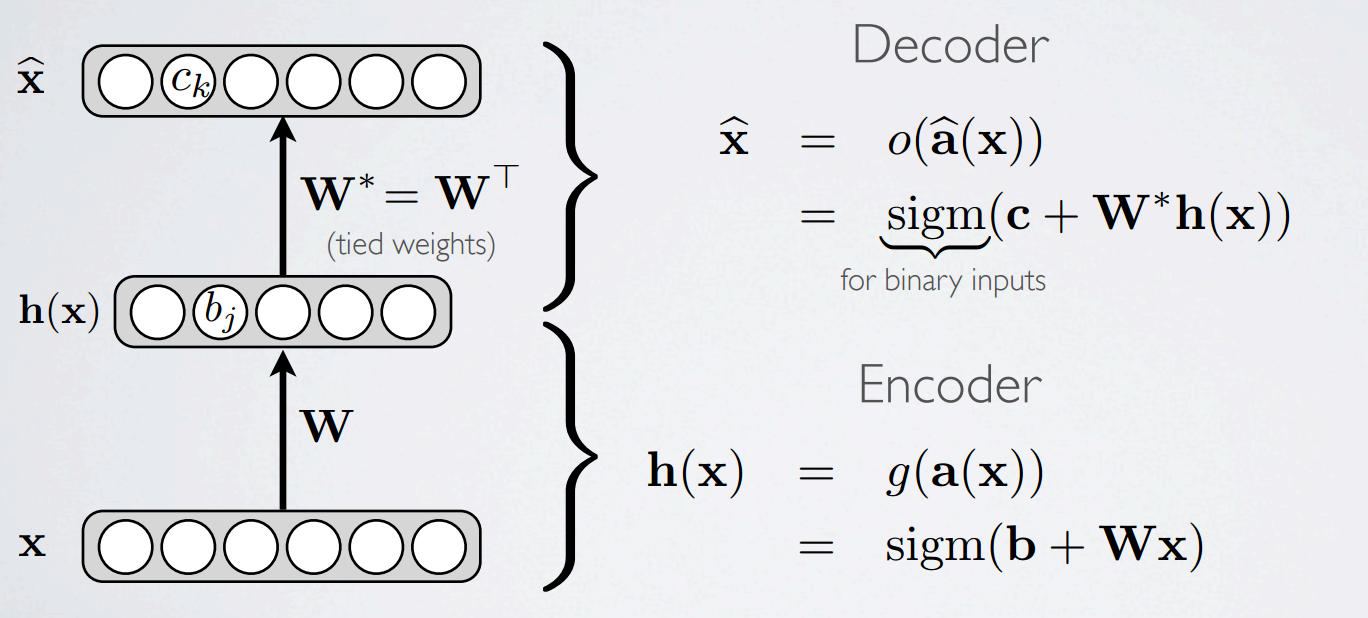
\[
L(f(x))=\frac{1}{2}\sum_k (\hat {x}_k-x_k)^2
\]
如果输入是binary的,即01值,那么就是
\[
L(f(x))=-\sum_k (x_k log(\hat{x}_k)+(1-x_k)log(1-\hat{x}_k))
\]PCA V.S. AutoEncoder

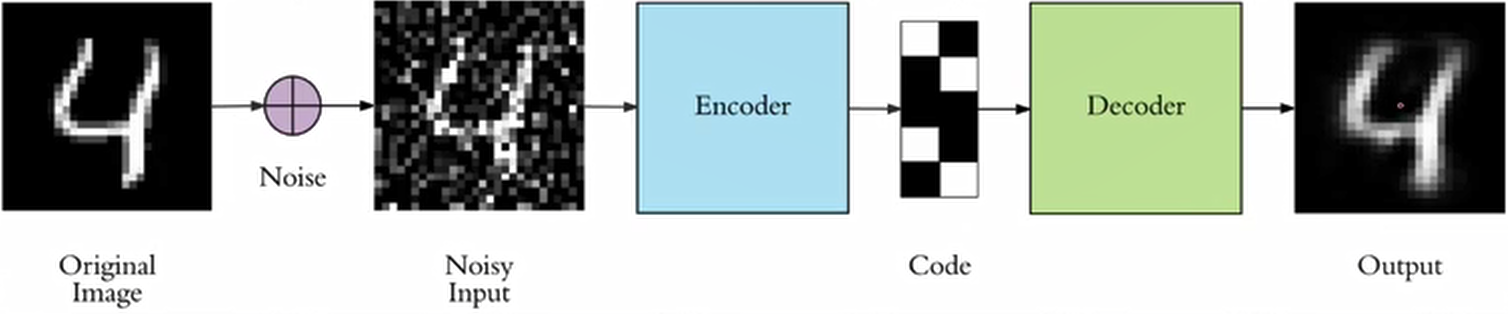
Denoising AutoEncoders
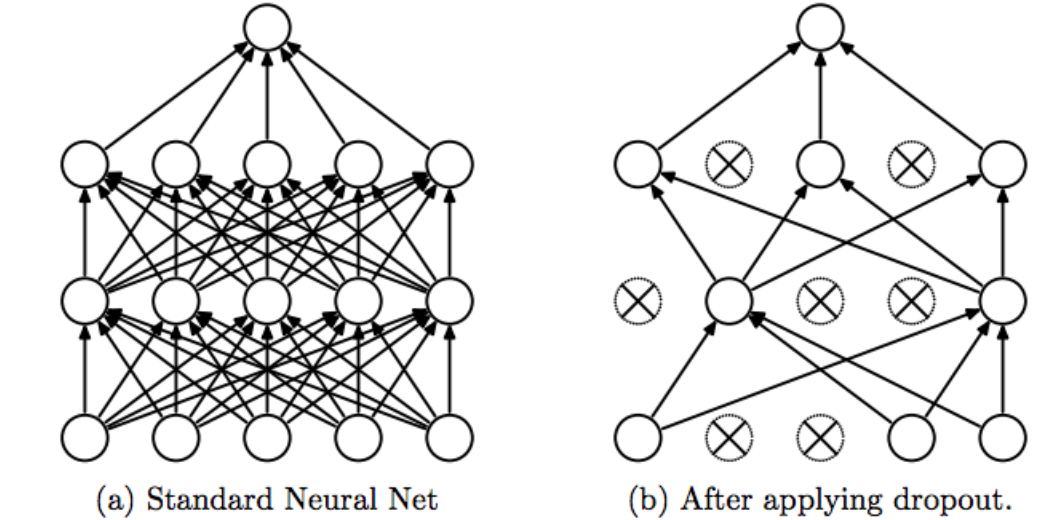
Dropout AutoEncoders
Adversarial AutoEncoders
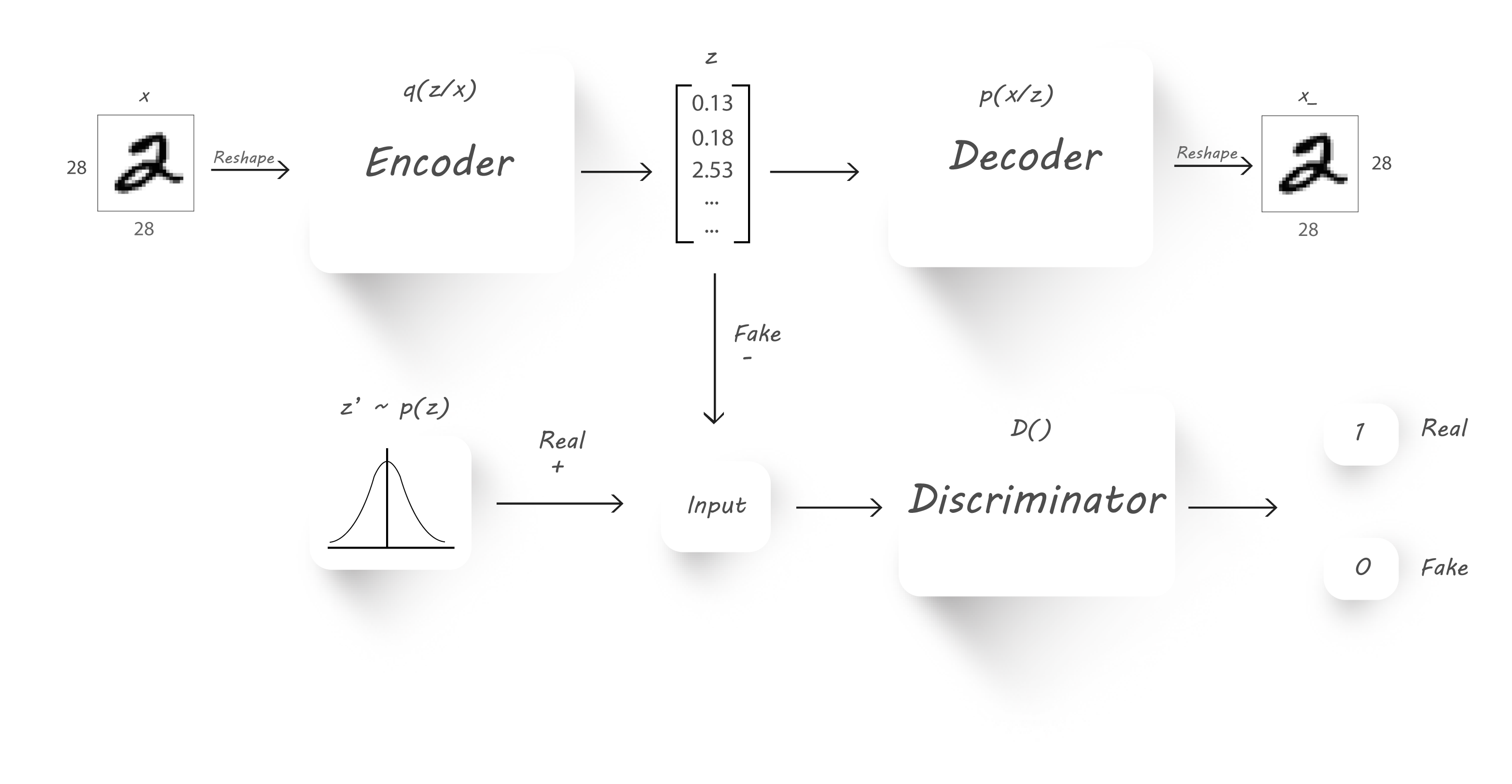
\[
{\cal L}\left( {x,\hat x} \right) + \sum\limits_j {KL\left( {{q_j}\left( {z|x} \right)||p\left( z \right)} \right)}
\]
其中\(KL(P||Q)=\int_{-\infty}^\infty{p(x)log\frac{p(x)}{q(x)}dx}\),如果\(P\)和\(Q\)分布非常接近,那么\(KL(P||Q)\approx 0\)。回过头看上面的Loss function就很好理解了,因为我们需要minimize loss,而且要求\(q(z)\)分布趋近于\(p(z)\)分布,而KL散度的作用正好是计算两个分布的相似程度
\[
\begin{align*}
KL(p,q) &= -\int {p(x)logq(x)dx}+\int {p(x)logp(x)dx}\&= \frac{1}{2}log(2\pi\sigma_2^2)+\frac{\sigma_1^2+(\mu_1-\mu_2)^2}{2\sigma_2^2}-\frac{1}{2}(1+log2\pi\sigma_1^2)\&=log\frac{\sigma_2}{\sigma_1}+\frac{\sigma_1^2+(\mu_1-\mu_2)^2}{2\sigma_2^2}-\frac{1}{2}
\end{align*}
\]
更加详细的推导过程可以看这篇文章Variational AutoEncoders
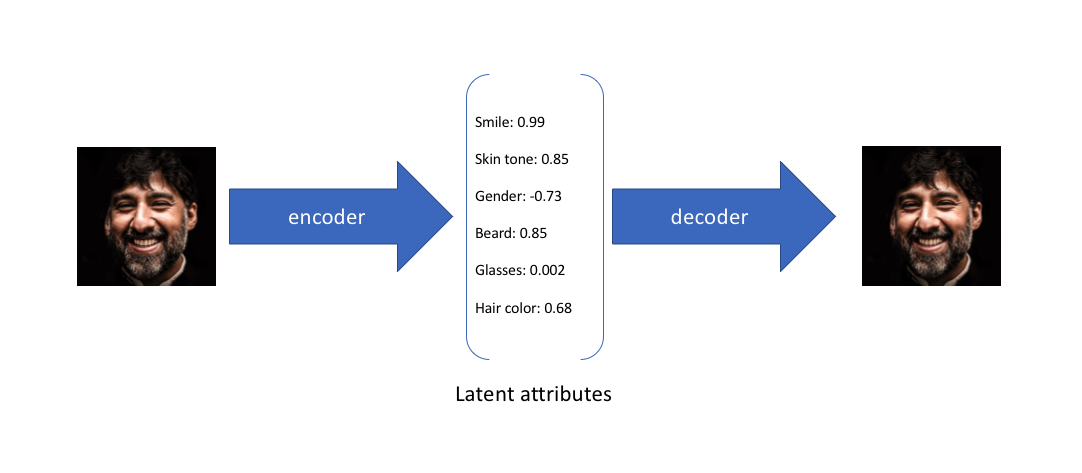
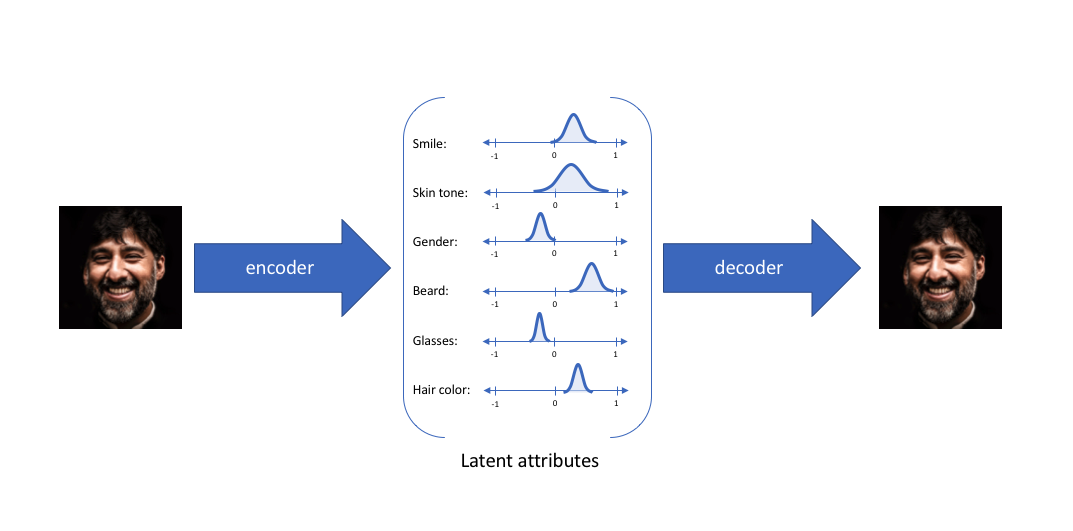
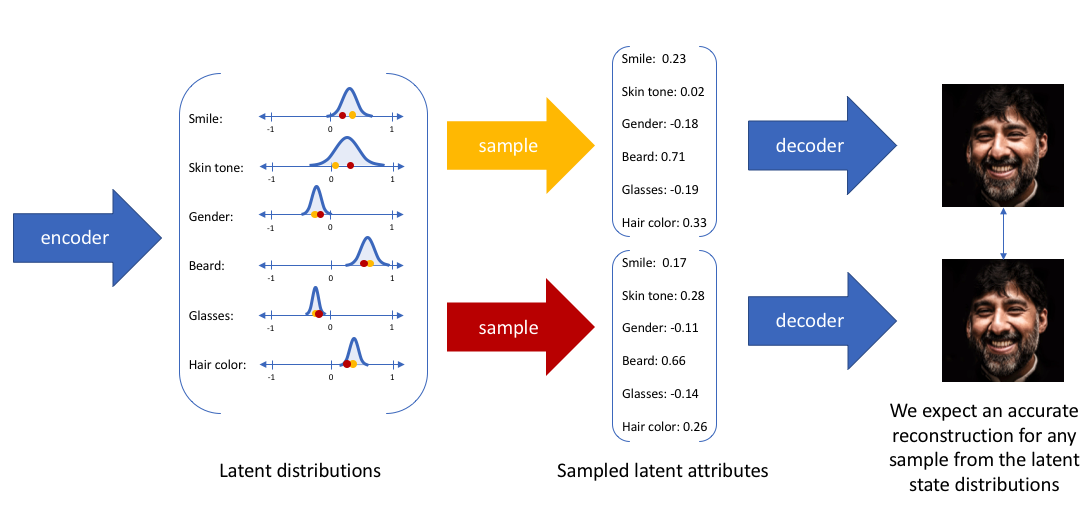
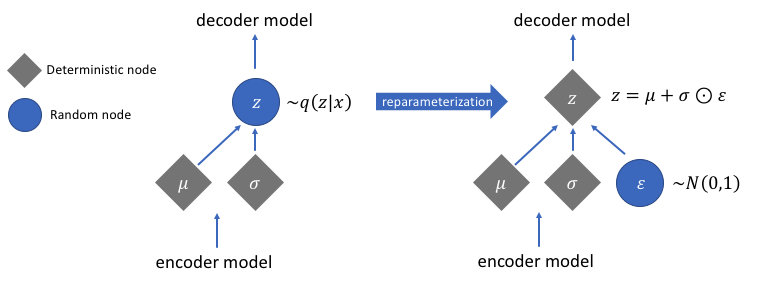
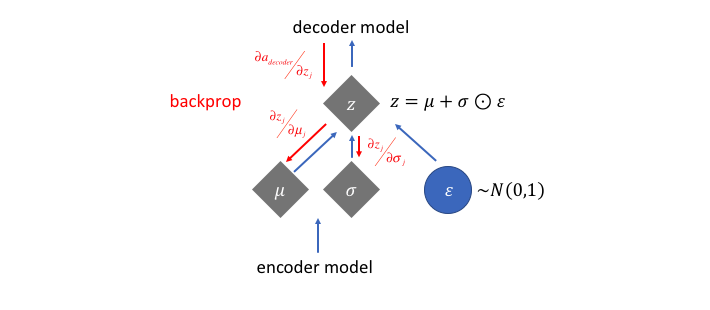
sample()是不能求导的,那我们如何反向传播?幸运的是,我们可以利用一个聪明的办法——"reparameterization trick"。这个办法的具体思想如下图,假设我们要让\(z\)服从正态分布,我们可以生成一个标准正态\(\varepsilon\),对这个标准正态进行平移以及伸缩变换,生成均值为\(\mu\),方差为\(\sigma\)的正态分布\(z=\mu+\sigma\odot \varepsilon\)