[APIO2009]采油区域

标签：fine   技术   pac   note   register   void   相交   矩形   amp   

https://zybuluo.com/ysner/note/1144701

题面

给出一个\(n×m\)的矩阵。请在其中选择\(3\)个互不相交的，大小恰为\(k×k\) 的子矩阵，使得子矩阵的权值和最大。

• \(n\leq1500,m\leq1500\)

  解析

  这题和CJOJ2501很像呢。。。
  看到题，本能地打了一个\(DP\)，然后至今调不出来。。。

解法一

矩阵对应端点为其右下方端点，\(S[i][j]\)即为其面积。
\(f[i][j]\)表示选择\((i,j)\)这个点对应矩阵，并且还选择\(1~0\)个矩阵的最优解。
\(upmx\)表示当前点可转移的上方所有点对应值\(S\)最优值。\(lfmx[j]\)表示前\(j\)列中的最优矩阵\(S\)值
那么有\(f[i][j]=max(upmx,lfmx[j-k])+S[i][j]\)
最巧妙的地方，我们最多可以选择3个矩阵，那么是不是可以看做选一个\(f[t1][t2]\)加上一个\(S[i][j]\)？
\(upmx\)表示当前点可转移的上方所有点对应值\(f\)最优值。\(lfmx[j]\)表示前\(j\)列中的最优矩阵\(f\)值
那么有\(ans[i][j]=max(upmx,lfmx[j-k])+S[i][j]\)

il void Matrix()
{
  fp(i,1,n) fp(j,1,m) a[i][j]=gi()+a[i-1][j]+a[i][j-1]-a[i-1][j-1];//二维前缀和套路
  fp(i,k,n) fp(j,k,m) s[i][j]=a[i][j]+a[i-k][j-k]-a[i-k][j]-a[i][j-k];//以(i,j)为右下端点的k*k矩阵的面积(还是套路,自己画图就知道了)
}
il void Solve()
{
  upmx=0;memset(lfmx,0,sizeof(lfmx));
  fp(i,k,n) 
    {
      fp(j,k,m) upmx=max(upmx,s[i-k][j]);//i代表行,j代表列,该矩阵上面 底最下到该矩形的上边的矩形
      fp(j,k,m) 
    {
          lfmx[j]=max(lfmx[j-1],lfmx[j]);//维护左边的最大权值矩形
          lfmx[j]=max(lfmx[j],s[i][j]);//维护上边的最大权值矩形
      f[i][j]=max(upmx,lfmx[j-k])+s[i][j];//累计合法情况
    }
    }//搞完两个矩阵的情况
  upmx=0;memset(lfmx,0,sizeof(lfmx));//lfmx变成维护f,f代表两个矩形,我们依据上面的套路继续选取s(1个)+f(2个)
 fp(i,k,n) 
    {
      fp(j,k,m) upmx=max(upmx,f[i-k][j]);
      fp(j,k,m) 
    {
          lfmx[j]=max(lfmx[j-1],lfmx[j]);
      lfmx[j]=max(lfmx[j],f[i][j]);
      ans=max(ans,max(upmx,lfmx[j-k])+s[i][j]);
    }
    }//搞完三个矩阵的矩阵
 //最后补充一句,在当前矩阵左上方选取的矩阵对当前矩阵没有影响
}
int main()
{
  n=gi();m=gi();k=gi();
  Matrix();
  ans=0;
  Solve();
  printf("%d\n",ans);
    return 0;
}

解法二

取三个互不相交的矩形？
何尝不是把整个图形分为三块，然后在每一块中取最大值？
分成三块有六种情况：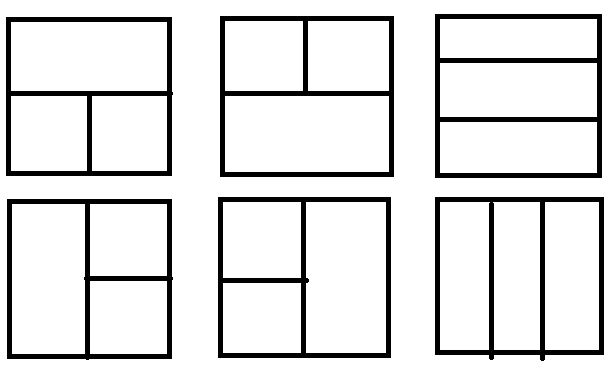

于是对应维护以每个点为右下角的\(k*k\)矩形权值和。
据此，可以维护每个点左上\(a\)、左下\(c\)、右上\(b\)、右下\(d\)部分的权值和。
然后枚举中间点（两条直线的交线，或者中间矩形的右下角），不断取\(max\)统计即可。

// luogu-judger-enable-o2
#include
#include
#include
#include
#include
#include
#define ll long long
#define re register
#define il inline
#define max(a,b) (a>b?a:b)
#define min(a,b) (a=b;i--)
using namespace std;
const int N=2100;
int n,m,k,mp[N][N],a[N][N],b[N][N],c[N][N],d[N][N],ans;
il int gi()
{
  re int x=0,t=1;
  re char ch=getchar();
  while((ch‘9‘)&&ch!=‘-‘) ch=getchar();
  if(ch==‘-‘) t=-1,ch=getchar();
  while(ch>=‘0‘&&ch

[APIO2009]采油区域

标签：fine   技术   pac   note   register   void   相交   矩形   amp   

原文地址：https://www.cnblogs.com/yanshannan/p/9028868.html