KMP算法
2021-04-13 09:28
标签:错误 变化 mp算法 lock 严格 复杂 out 内容 href 给定文本串A、模式串B,求模式串B在文本串A中出现的次数。 设文本串A的长度为n,模式串B的长度为m 暴力:二重循环+回溯 复杂度 O(n*m) KMP: 将复杂度优化到O(n+m) 本篇文章是我初学KMP算法所写,如果有错误欢迎指出 另外本文的KMP算法的实现方式较常规的实现效率似乎低一些,我在网上看到大多数博客在求prefix数组时似乎没有用到递归。关于KMP算法的不同的实现、KMP算法的扩展算法我会在后期补充进来。 许多题目对于前缀与真前缀的区分并不严格。准确来讲,真前缀为前缀的子集。 如字符串ABCD 其前缀有 真前缀有 对于字符串AABBAAB 其最长公共真前后缀为 暴力求解的时间浪费在匹配失败后回溯头指针的过程中,KMP的本质其实也在头进行指针回溯,但是KMP能够使得头指针尽可能的回溯至少量,从而减少算法时间。 prefix数组,是指由B串的每一种子串的最长公共真前后缀长度所构成的数组。 prefix[i]即:长度为i的模式串的最长公共前后缀 如模式串abbabbaaba 因此有 prefix: -1 0 0 0 1 2 3 4 1 2 注意,定义prefix[0] = -1 (后面解释为什么) 使得头指针尽可能的回溯至少量,从而减少算法时间。 我们以上图中的匹配为例。假设当前正在将文本串的b与模式串的a进行匹配。发现二者不相同,此时应该将模式串整体向右移动。对于暴力解法,只会向右移动一格,然后从模式串的第一位开始向后一一匹配。在KMP中,由于我们已经求出了prefix数组,prefix[6] = 3,这表明,前面长度为6的子串abbabb的前3位和后3位是相同的。由于abbabb这一段是模式串与文本串匹配成功的,因此可以确定文本串b前的6位也应该是abbabb 对于模式串的真前缀abb,可以将其移动到文本串中原本和模式串的真后缀abb匹配的位置,即: 这个操作的复杂度是O(1)的,原因我们后面会讲到 求prefix数组这件事本身就不是一个容易的过程。如果暴力求解,其复杂度仍然是O(\(m^2\))。一种常见的高效求解prefix数组的方式是DP 对于模式串abbabbaab 假设已经求出prefix[5] = 2,现在要求prefix[6],只需要检验第3个字母(pattern[2])是否和第6位字母(pattern[5])相同。原因在于,已经知道了prefix[5] = 2,即patter[0~1]的ab已经和pattern[3~4]的ab匹配,只需要再检验pattern[2]的b和pattern[5]的b匹配,就能得到pattern[0~2]的abb和pattern[3~4]的abb匹配。 因此得到状态转移方程之一 对于模式串abbabbaab 假设已经求出prefix[0~7] 现在要求prefix[8]。因为 pattern[7] = a pattern[prefix[7]] = b,二者不相等。故设置比较指针 为什么让 图中的紫色指针为 第一次 ptr = 4 ,将 发现二者不同之后,需要找长度较小的公共真前后缀检验能否再次变长 由于ptr = 4,因此可以确定的是真前缀 第一个 因此只需要比较第一个 如果相同,循环结束;否则重复 不知道是否讲清楚了。ptr的变化过程,实际上可以理解为公共真前后缀不断缩短的过程。 最后要么在缩短到1的过程发现匹配成功,要么缩短到0(此时ptr = -1) 下面是求prefix数组的完整代码 这一段的内容与 算法的执行过程中,需要时刻维护两个指针, Input abbaabbcabbacabbaabbabba abba Output 共有5次匹配 0 8 13 17 20 参考 https://blog.csdn.net/v_JULY_v/article/details/7041827 KMP算法 标签:错误 变化 mp算法 lock 严格 复杂 out 内容 href 原文地址:https://www.cnblogs.com/popodynasty/p/13343243.htmlKMP算法
预备知识
前缀与真前缀
A AB ABC ABCDA AB ABC最长公共真前后缀
AAB (AABBAAB / AABBAAB)算法思路介绍
什么是prefix数组
模式串B的子串
prefix[i]
真前缀
a
prefix[1] = 0
(null)
ab
prefix[2] = 0
(null)
abb
prefix[3] = 0
(null)
abba
prefix[4] = 1
a
abbab
prefix[5] = 2
ab
abbabb
prefix[6] = 3
abb
abbabba
prefix[7] = 4
abba
abbabbaa
prefix[8] = 1
a
abbabbaab
prefix[9] = 2
Ab
求prefix数组的目的
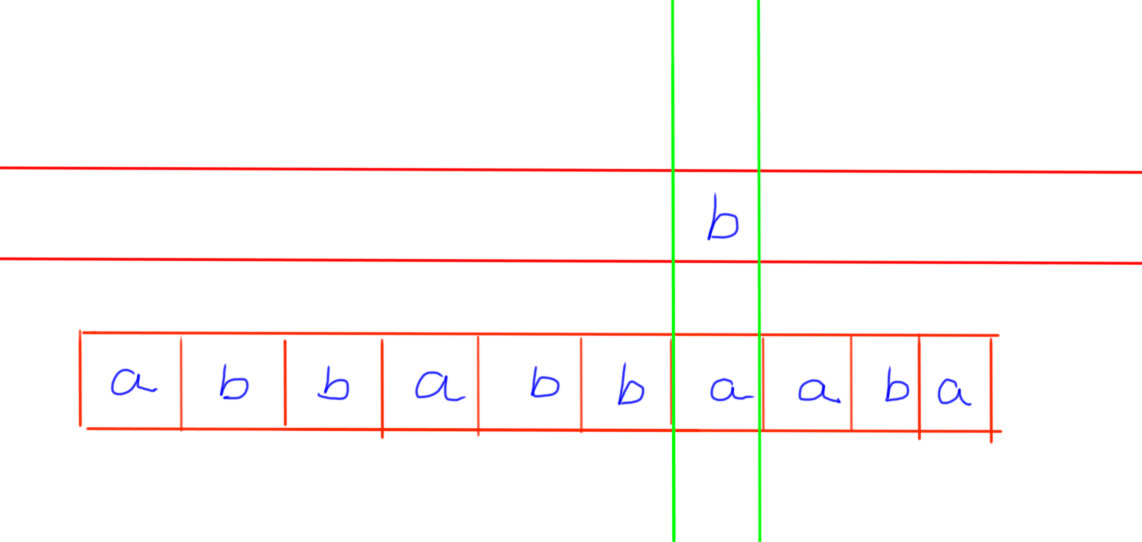
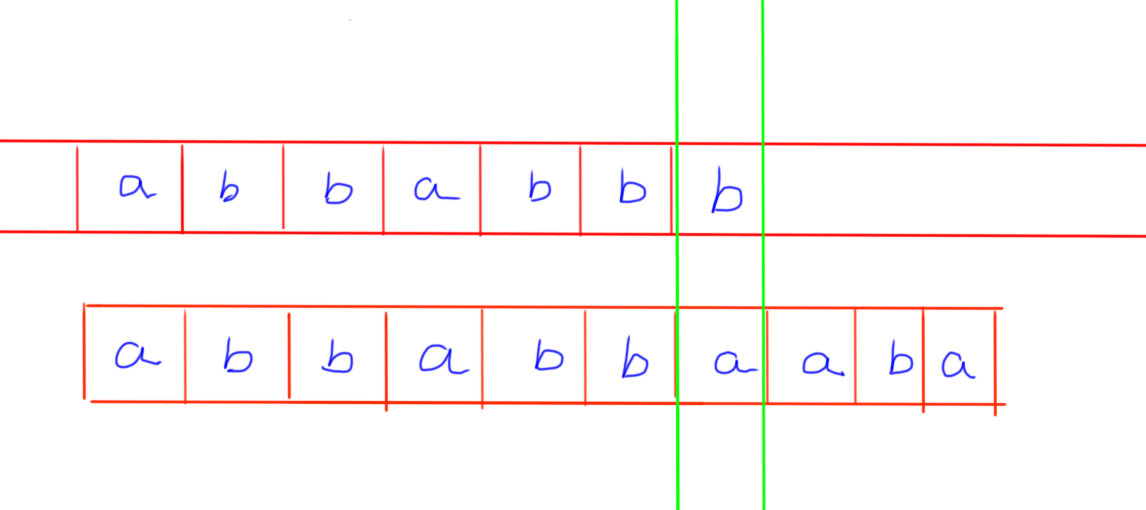
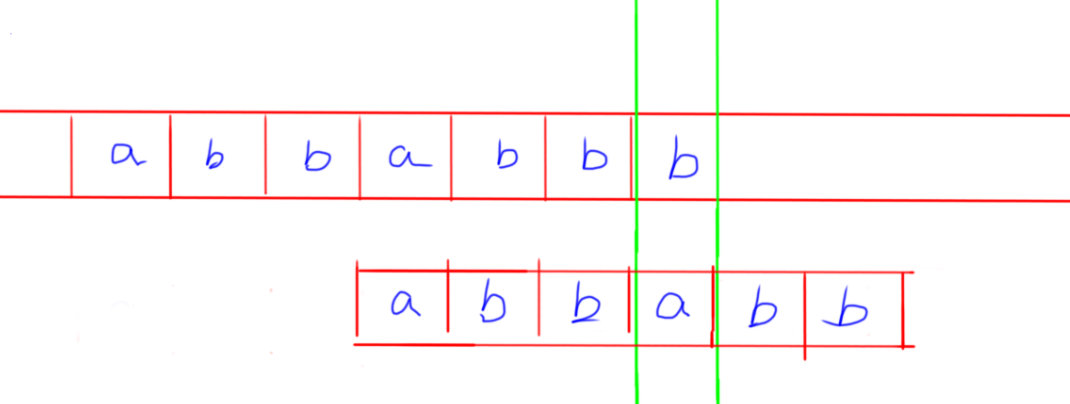
如何求prefix数组
如何得到状态转移方程?
if(pattern[i-1] == pattern[prefix[i-1]]){
prefix[i] = prefix[i-1] + 1;
}
模式串B的子串
prefix[i]
真前缀
a
prefix[1] = 0
(null)
ab
prefix[2] = 0
(null)
abb
prefix[3] = 0
(null)
abba
prefix[4] = 1
a
abbab
prefix[5] = 2
ab
abbabb
prefix[6] = 3
abb
abbabba
prefix[7] = 4
abba
ptr = prefix[i-1] 。while(ptr >= 0 && pattern[i-1] != pattern[ptr]){
ptr = prefix[ptr];
}
ptr = prefix[ptr] ?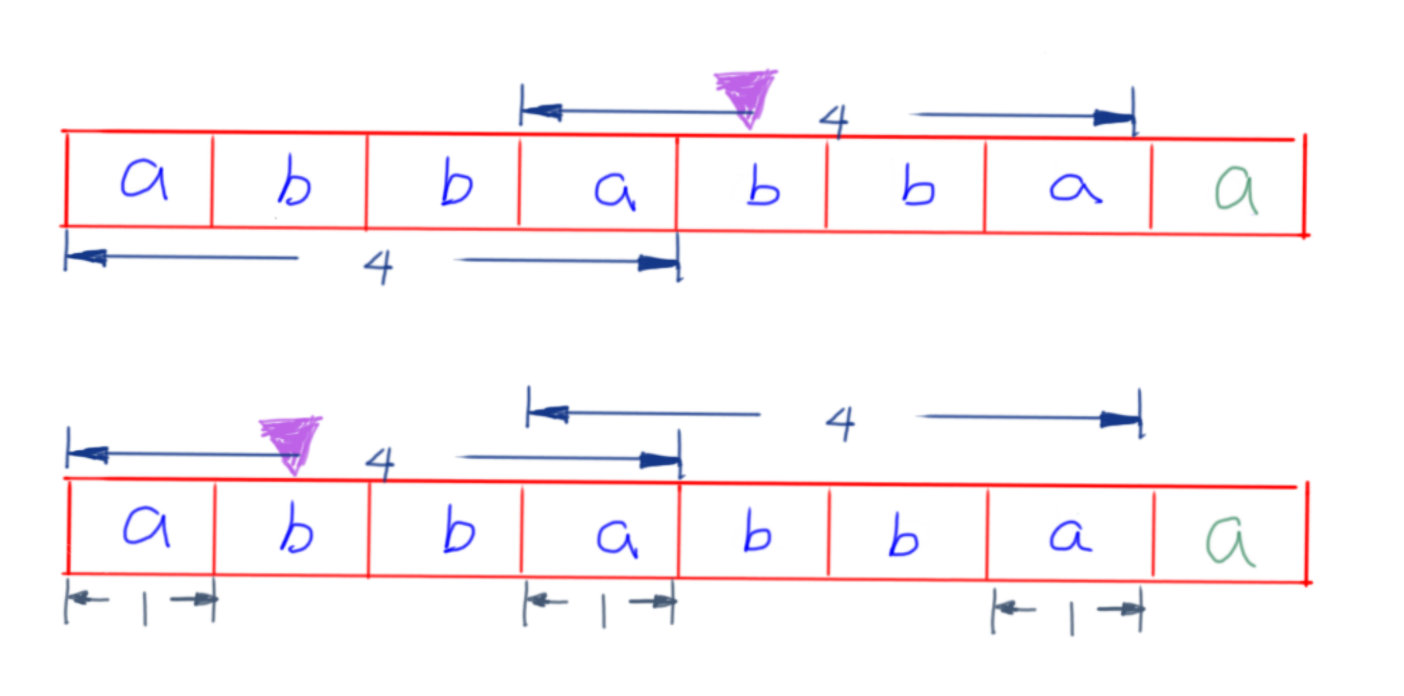
ptr两次所指向的位置,分别为 pattern[4] 和 pattern[1]a 与 pattern[ptr] 比较,其原因是检验长度为4的公共真前后缀能否继续变长abba与真后缀abba匹配abba的真前缀a,与第二个abba的真后缀相同abba的真前缀a的下一个字母和第二个abba的真后缀a的下一个字母ptr = prefix[ptr]#define MaxM 20+5
char pattern[MaxM];
int prefix[MaxM];
void get_prefix(int size){
prefix[0] = -1;
prefix[1] = 0;
for (int i = 2; i = 0 && pattern[i-1] != pattern[ptr]) {
ptr = prefix[ptr];
}
if(ptr == -1){
prefix[i] = 0;
}else{
prefix[i] = ptr + 1;
}
}
}
}
开始匹配
求prefix数组的目的 其实是一样的。求prefix数组的目的就在于降低后期匹配的复杂度。既然知道了其降低复杂度的方式(如果还不明白,请重新看一遍求prefix数组的目的,本版块不再重复介绍),写出匹配的代码也就十分容易。i 和ji时刻指向文本串的待匹配字符,j时刻指向模式串的待匹配字符void match(char text[],char pattern[],int text_size,int pattern_size,vector完整代码
#include 测试数据