C# 定积分求周长&面积原理 代码实现
2021-04-13 11:40
标签:活性 三个点 控制 double 巩固 插件 技术分享 灵活 art 前言: 前些日子,因为工作原因,接触到了求解曲线周长,真的是搞了很久,学生时代真的很简单,但是如今的我来说,忘记了....很多人跟我应该一样。 所以来巩固加强一下记忆。一开始的时候,求周长嘛,找公式呗,什么matlab呀,乱七八糟的,晕,最后找到了可能还不能满足项目的需求,因为可能计算量过大。(我就是这样子的,灵活性相对较低) 还有就是明明自己可以用代码实现,为什么非要插件,工具呐,这么不自信的? 所以,“一怒之下”,自己去看了一下定积分求周长的原理,自己还是用代码来实现吧。 (以下内容纯是个人这段时间的理解,如果有错误的,欢迎指正出来。) 首先需要说说两个概念,曲线和周长,因为我们要求他们嘛。 这个世界,有曲线吗?我的回答是,没有。那...这...曲线是由无数个直接拼接而成。再准确的说无数个很短的曲线拼接而成。 (如果您彻底理解了这句话,后面就不用看了,基本就没了。) 与周长的概念类似,没有正方形,没有圆形。只有三角形,所有的图形都是三角形拼接而成。而两个三角形拼成长方形,而我们的面积是由无数个长方形,拼接而成。 (定积分原理的参考图) testCount,即自定义的测试数量,可以理解为精细度,值越大,计算量越大,数据越准确,这个可看你项目需求精细度,通过该变量 可在实现最少的计算量情况,实现你要的效果。 eachX,就是你的曲线被分成N份,每份的长度。 curY,当前点的y轴分量 previousY,上一个点的y轴分量, curLength,即如图 (剩余的部分,代码里面含解释,个人喜欢放在源码里面,原生的,纯24k原创) 补充:这边,我对贝塞尔曲线做一下补充吧。因为我因为什么幂函数,指数函数遇到的肯,因为这些函数毕竟还不是那么灵活,都具有一定“规律”。 贝塞尔曲线的灵活,受6个参数控制,三个点嘛。(二维空间) 详情可参考这篇:http://www.sohu.com/a/118656687_466876 C# 定积分求周长&面积原理 代码实现 标签:活性 三个点 控制 double 巩固 插件 技术分享 灵活 art 原文地址:https://www.cnblogs.com/u3ddjw/p/8945782.html曲线:
面积:
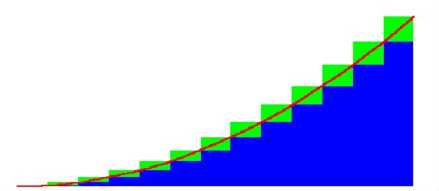
源码实现:
double GetLength(float start,float end)
{
double sumLength = 0;
float eachX = (end - start) / testCount;
for (int i = 1; i )
{
double curY =ArcFunction(start+eachX*i);
double previousY = ArcFunction(start+eachX*(i-1));
//根据c2=a2+b2
double curLength = Math.Sqrt(Math.Pow(eachX, 2) + Math.Pow(curY - previousY, 2));
sumLength += curLength;
}
return sumLength;
}
解释: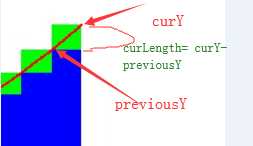
1 int testCount = 1000; //所谓的测试细致度吧,可动态调控,你自己掌握。
2 ///
文章标题:C# 定积分求周长&面积原理 代码实现
文章链接:http://soscw.com/index.php/essay/75177.html