【网络流】Dinic算法理解
2021-04-15 16:28
标签:false 大于 cto scanf return 解决 front layer 判断 EK算法还是不够优秀,我们还是要学习更加优秀的Dinic算法才能解决更多要求较高的问题。 这里确保大家都是懂得网络流的一些基本概念的,如果不懂的,这里有一个链接,大家可以看一看。网络流详解(显然不是我写的!) 他的EK算法比我写的好看的多,强势给大家安利一波!!! 同时大家可以注意下这张图,结合链接中的讲解认真理解一下就可以懂得为什么要反向连边的原理! 就是给你一次反悔的机会,类似于我们搜索时改变当前层的一个变量,后面又要把他改回来!!! 这里转载一下EK算法和Dinic算法的一些算法大体实现思想 在一般的增广路算法中, 程序的实现过程与增广路求最大流的过程基本一致. 即每一次更新都进行一次找增广路然后更新路径上的流量的过程。但是我们可以从上图中发现一个问题, 就是每次找到的增广路曲曲折折非常长, 此时我们往往走了冤枉路(即:明明我们可以从源点离汇点越走越进的,可是中间的几条边却向离汇点远的方向走了), 此时更新增广路的复杂度就会增加。EK 算法为了规避这个问题使用了 bfs 来寻找增广路, 然后在寻找增广路的时候总是向离汇点越来越近的方向去寻找下一个结点。 借用一下代码: 邻接矩阵实现: 邻接表实现: 每进行一次增广需要的时间复杂度为 bfs 的复杂度 + 更新残余网络的复杂度, 大约为 O(m)(m为图中的边的数目), 需要进行多少次增广呢, 假设每次增广只增加1, 则需要增广 nW 次(n为图中顶点的数目, W为图中边上的最大容量), . 敲黑板 算法思想 DINIC 在找增广路的时候也是找的最短增广路, 与 EK 算法不同的是 DINIC 算法并不是每次 bfs 只找一个增广路, 他会首先通过一次 bfs 为所有点添加一个标号, 构成一个层次图, 然后在层次图中寻找增广路进行更新。 算法流程 利用 BFS 对原来的图进行分层,即对每个结点进行标号, 这个标号的含义是当前结点距离源点的最短距离(假设每条边的距离都为1),注意:构建层次图的时候所走的边的残余流量必须大于0 用 DFS 寻找一条从源点到汇点的增广路, 注意: 此处寻找增广路的时候要按照层次图的顺序, 即如果将边(u, v)纳入这条增广路的话必须满足, 其中 为结点 的编号。找到一条路后要根据这条增广路径上的所有边的残余流量的最小值更新所有边的残余流量(即正向弧 - l, 反向弧 + l). 重复步骤 2, 当找不到一条增广路的时候, 重复步骤 1, 重新建立层次图, 直到从源点不能到达汇点为止。 其实实现还是非常简单的,下面放一篇本人AC的代码,然后我再来讲一讲里面要注意的一些细节。(注意上面是BFS找1条,只有1条!!!) 我们最容易写错的东西其实就是dfs(),首先要注意就是每次dfs下去找最小的边的时候,一定要保证最小边不是0,如果是0,但是不判断的话,他就会一直把一个没有用的标记进行上传,非常的浪费时间。 最后如果增广失败不要忘记返回0(return 0),否则程序会出现奇怪的错误。 记住用链式前向星的与图论的链式前向星的一些不同的地方!还有反向弧减边的技巧。 下面给出一道板题和AC代码:大家仅供参考: 题目链接: AC code: 【网络流】Dinic算法理解 标签:false 大于 cto scanf return 解决 front layer 判断 原文地址:https://www.cnblogs.com/mudrobot/p/13329111.html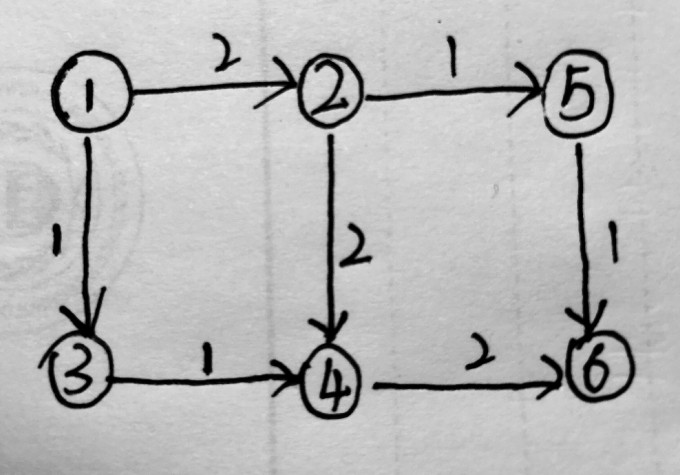
一般增广路算法(EdmondsKarp)
#include const int MAXN = 430;
const int MAX_INT = (1 que;
memset(vis, 0, sizeof(vis));
memset(pre, -1, sizeof(pre));
pre[s].v = s;
vis[s] = true;
que.push(s);
while(!que.empty()){
int u = que.front();
que.pop();
for(int i = head[u]; i + 1; i = edge[i].nxt){
int v = edge[i].v;
if(!vis[v] && edge[i].w){
pre[v].v = u;
pre[v].id = i;
vis[v] = true;
if(v == t) return true;
que.push(v);
}
}
}
return false;
}
int EK(int s, int t){
int ans = 0;
while(bfs(s, t)){
int mi = MAX_INT;
for(int i = t; i != s; i = pre[i].v){
mi = min(mi, edge[pre[i].id].w);
}
for(int i = t; i != s; i = pre[i].v){
edge[pre[i].id].w -= mi;
edge[pre[i].id ^ 1].w += mi;
}
ans += mi;
}
return ans;
}
// 加边
addEdge(u, v, w);
addEdge(v, u, 0);
// 调用
int ans = EK(s, t);
算法复杂度
Dinic 算法
#include注意:
P2740 [USACO4.2]草地排水Drainage Ditches#include