c#数字图像处理(七)直方图匹配
2021-04-19 23:29
阅读:903
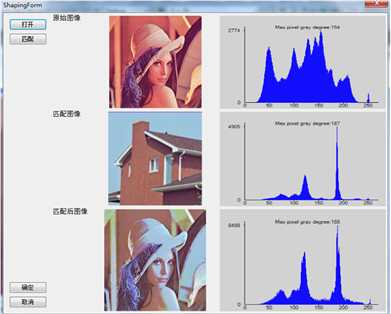
直方图匹配,又称直方图规定化,即变换原图的直方图为规定的某种形式的直方图,从而使两幅图像具有类似的色调和反差。直方图匹配属于非线性点运算。
直方图规定化的原理:对两个直方图都做均衡化,变成相同的归一化的均匀直方图,以此均匀直方图为媒介,再对参考图像做均衡化的逆运算

////// 直方图匹配 /// /// 原始图像 /// 匹配图像 /// 处理后图像 /// 处理成功 true 失败 false public static bool HistogramMatching(Bitmap srcBmp, Bitmap matchingBmp, out Bitmap dstBmp) { if (srcBmp == null || matchingBmp == null) { dstBmp = null; return false; } dstBmp = new Bitmap(srcBmp); Bitmap tempSrcBmp = new Bitmap(srcBmp); Bitmap tempMatchingBmp = new Bitmap(matchingBmp); double[] srcCpR = null; double[] srcCpG = null; double[] srcCpB = null; double[] matchCpB = null; double[] matchCpG = null; double[] matchCpR = null; //分别计算两幅图像的累计概率分布 getCumulativeProbabilityRGB(tempSrcBmp, out srcCpR, out srcCpG, out srcCpB); getCumulativeProbabilityRGB(tempMatchingBmp, out matchCpR, out matchCpG, out matchCpB); double diffAR = 0, diffBR = 0, diffAG = 0, diffBG = 0, diffAB = 0, diffBB = 0; byte kR = 0, kG = 0, kB = 0; //逆映射函数 byte[] mapPixelR = new byte[256]; byte[] mapPixelG = new byte[256]; byte[] mapPixelB = new byte[256]; //分别计算RGB三个分量的逆映射函数 //R for (int i = 0; i 256; i++) { diffBR = 1; for (int j = kR; j 256; j++) { //找到两个累计分布函数中最相似的位置 diffAR = Math.Abs(srcCpR[i] - matchCpR[j]); if (diffAR - diffBR 1.0E-08) {//当两概率之差小于0.000000001时可近似认为相等 diffBR = diffAR; //记录下此时的灰度级 kR = (byte)j; } else { kR = (byte)Math.Abs(j - 1); break; } } if (kR == 255) { for (int l = i; l 256; l++) { mapPixelR[l] = kR; } break; } mapPixelR[i] = kR; } //G for (int i = 0; i 256; i++) { diffBG = 1; for (int j = kG; j 256; j++) { diffAG = Math.Abs(srcCpG[i] - matchCpG[j]); if (diffAG - diffBG 1.0E-08) { diffBG = diffAG; kG = (byte)j; } else { kG = (byte)Math.Abs(j - 1); break; } } if (kG == 255) { for (int l = i; l 256; l++) { mapPixelG[l] = kG; } break; } mapPixelG[i] = kG; } //B for (int i = 0; i 256; i++) { diffBB = 1; for (int j = kB; j 256; j++) { diffAB = Math.Abs(srcCpB[i] - matchCpB[j]); if (diffAB - diffBB 1.0E-08) { diffBB = diffAB; kB = (byte)j; } else { kB = (byte)Math.Abs(j - 1); break; } } if (kB == 255) { for (int l = i; l 256; l++) { mapPixelB[l] = kB; } break; } mapPixelB[i] = kB; } //映射变换 BitmapData bmpData = dstBmp.LockBits(new Rectangle(0, 0, dstBmp.Width, dstBmp.Height), ImageLockMode.ReadWrite, PixelFormat.Format24bppRgb); unsafe { byte* ptr = null; for (int i = 0; i ) { ptr = (byte*)bmpData.Scan0 + i * bmpData.Stride; for (int j = 0; j ) { ptr[j * 3 + 2] = mapPixelR[ptr[j * 3 + 2]]; ptr[j * 3 + 1] = mapPixelG[ptr[j * 3 + 1]]; ptr[j * 3] = mapPixelB[ptr[j * 3]]; } } } dstBmp.UnlockBits(bmpData); return true; } /// /// 计算各个图像分量的累计概率分布 /// /// 原始图像 /// R分量累计概率分布 /// G分量累计概率分布 /// B分量累计概率分布 private static void getCumulativeProbabilityRGB(Bitmap srcBmp, out double[] cpR, out double[] cpG, out double[] cpB) { if (srcBmp == null) { cpB = cpG = cpR = null; return; } cpR = new double[256]; cpG = new double[256]; cpB = new double[256]; int[] hR = null; int[] hG = null; int[] hB = null; double[] tempR = new double[256]; double[] tempG = new double[256]; double[] tempB = new double[256]; getHistogramRGB(srcBmp, out hR, out hG, out hB); int totalPxl = srcBmp.Width * srcBmp.Height; for (int i = 0; i 256; i++) { if (i != 0) { tempR[i] = tempR[i - 1] + hR[i]; tempG[i] = tempG[i - 1] + hG[i]; tempB[i] = tempB[i - 1] + hB[i]; } else { tempR[0] = hR[0]; tempG[0] = hG[0]; tempB[0] = hB[0]; } cpR[i] = (tempR[i] / totalPxl); cpG[i] = (tempG[i] / totalPxl); cpB[i] = (tempB[i] / totalPxl); } } /// /// 获取图像三个分量的直方图数据 /// /// 图像 /// R分量直方图数据 /// G分量直方图数据 /// B分量直方图数据 public static void getHistogramRGB(Bitmap srcBmp, out int[] hR, out int[] hG, out int[] hB) { if (srcBmp == null) { hR = hB = hG = null; return; } hR = new int[256]; hB = new int[256]; hG = new int[256]; BitmapData bmpData = srcBmp.LockBits(new Rectangle(0, 0, srcBmp.Width, srcBmp.Height), ImageLockMode.ReadOnly, PixelFormat.Format24bppRgb); unsafe { byte* ptr = null; for (int i = 0; i ) { ptr = (byte*)bmpData.Scan0 + i * bmpData.Stride; for (int j = 0; j ) { hB[ptr[j * 3]]++; hG[ptr[j * 3 + 1]]++; hR[ptr[j * 3 + 2]]++; } } } srcBmp.UnlockBits(bmpData); return; }
评论
亲,登录后才可以留言!