概率图：HMM：Learning问题（EM算法）
2021-04-21 03:29
标签：问题 约束 info 资料 VID shu 参数表 src width 一：问题描述 Learning问题就是参数估计问题，也就是求模型参数λ，具体形式为 ：λ_hat=argmax P(O|λ) 【通过最大化似然求得最优模型参数 λ；优化算法用EM，可类比GMM模型中求θ用的EM】 二、EM算法应用于HMM-learning模型的公式推导（具体可参考之前博客GMM：EM） （来源：B站up主，shuhuai008,板书） 备注： ①最后求出 ②将EM算法应用于HMM算法的求解，其实就是引入EM算法的公式（用HMM的参数表达），另外加上拉格朗日乘子法得到λ=（Π,A,B）的迭代公式 用HMM参数表达的EM算法 公式推导中的关键小技巧： ③积分求和与条件概率=> 化简公式 ④隐含约束：Σ1NΠi=1 ⑤EM算法表达为求解最大值形式：argmax，带上隐含约束即为带约束的最值问题，自然地想到用拉格朗日乘子法求解。 参考资料： 1.https://www.bilibili.com/video/BV1MW41167Rf?p=5。作者：shuhuai008 概率图：HMM：Learning问题（EM算法） 标签：问题 约束 info 资料 VID shu 参数表 src width 原文地址：https://www.cnblogs.com/feynmania/p/13282639.html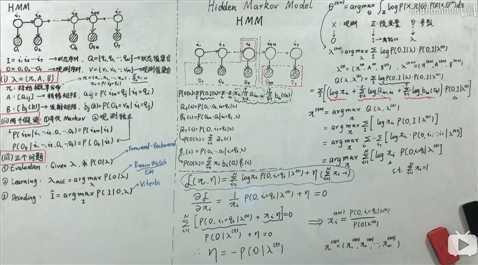
后，需要再代回
，最后得到t+1时刻的Π值。【拉格朗日乘子法也可以用于求数值解】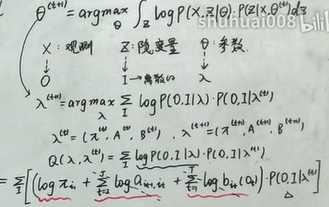
上一篇：树状数组
文章标题：概率图：HMM：Learning问题（EM算法）
文章链接：http://soscw.com/index.php/essay/77430.html