堆排序的时间复杂度分析
2021-04-22 18:28
标签:计算 复杂 load 分析 基本 nbsp alt max 次数 堆排序分为两步,即初始化堆、调整堆。 两个步骤都要调用一个调整结点顺序的函数,以大根堆为例,操作为: 1:如果父亲结点num[a]和它的两个孩子结点num[2a+1], num[2a+2]满足um[a] > max{num[2a+1], num[2a+2]},那么返回; 2:如果不满足堆的性质,那么将父亲结点num[a]和较大孩子结点max{num[2a+1], num[2a+2]}交换, 3:将原来较大的孩子结点作为父亲结点,重复上述操作,直到孩子结点是叶子结点为止 初始化堆的时间复杂度分析 初始化堆的时候,对于每个非叶子结点,都要调用上述函数,将它与它的孩子结点进行比较和交换,顺序是从后向前。 以操作2作为基本操作,对每一层都完全铺满的堆进行分析, 设元素个数为n,则堆的高度k=log(n+1)≈log n,非叶子结点的个数为2^(k-1)-1 假设每个非叶子结点都需要进行调整,则第i层的非叶子结点需要的操作次数为k-i, 第i层共有2^(i-1)个结点,则第i层的所有结点所做的操作为k*2^(i-1)- i*2^(i-1), 共k-1层非叶子结点,总的操作次数为 化简可得,上式=2^k-k+1,将k=log(n+1)≈log n代入,得n - log n +1, 所以,初始化堆的复杂度为O(n) 调整堆的时间复杂度分析 调整堆的复杂度计算和初始化堆差不多, 假设根节点和排在最后的序号为m的叶子结点交换,并进行调整,那么调整的操作次数 = 原来m结点所在的层数 = 堆的高度(因为m结点在堆的最后)= log m 共n个结点,调整的总操作次数为 化简可得,上式=log (n-1)! ≈ n*log n 所以,调整堆的复杂度为O(n*log n) 所以,总体复杂度为O(n*log n) 堆排序的时间复杂度分析 标签:计算 复杂 load 分析 基本 nbsp alt max 次数 原文地址:https://www.cnblogs.com/lylhome/p/13276081.html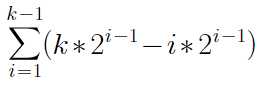
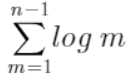
下一篇:[C]enum类型