快速排序
2021-04-23 06:29
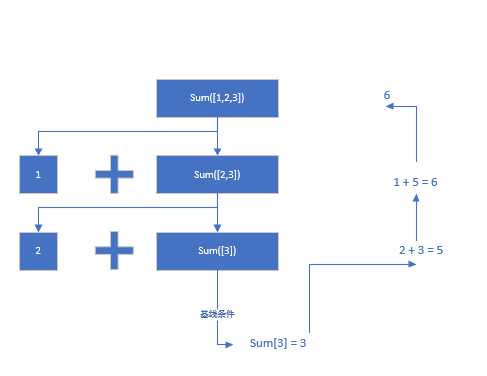
标签:count list 简单 数字 原理 条件 mamicode 数组 分而治之 本篇内容共分两部分:分而治之,快速排序。 分而治之(divide and conquer,D & C)——种著名得递归式问题解决办法。 快速排序是一种排序算法其速度比选择排序快得多。 1. 分而治之 首先,我们申明一下D&C的工作原理: 接下来通过一个例子来说明分而治之思想。 假设,我们求数组 我们首先使用循环来实现一下: 接下来我们讲述用递归来实现。 我们需要找出基线条件。既然我们要对数组求和,那么最简单的数组怎么样的呢? 这就是基线条件。 接下来的问题就是如何缩小问题的规模。 sum([1,2,3]) = 6 --> 1 + sum([2,3]) --> 1 + 2 + sum([3]) 其工作原理类似如下: 留下几个练习(答案在最后面): 2. 快速排序 通过前面的了解,我们可以知道,基线条件是数组为空或者只包含一个元素。在这种情况下,只需要返回数组——根本不用排序。 接下来,我们看看对两个元素的数组进行排序。 [1, 3] 我们检查第一个元素是否比第二个元素小,否则就交换位置。 如果是三个元素呢? [2,1,3] 因为我们需要使用D&C,因此需要将数组进行分解,直到满足基线条件。下面介绍快速排序的工作原理。首先,从数组选择一个元素,这个元素被称为基准值(pivot),可以是数组的任何一个元素。 接下来,找出比基准值小的元素以及比基准值大的元素。 我们选择[2]为基准值,则 [1] [2] [3]。 这被称为分区。现在你有: 得到的两个子数组若是有序的,则可以合并成一个有序的数组。否则,就在子数组中按照以上方法继续执行,直到有序或者满足基线条件。 下面是代码: 答案 快速排序 标签:count list 简单 数字 原理 条件 mamicode 数组 分而治之 原文地址:https://www.cnblogs.com/JonnyJiang-zh/p/13270155.html快速排序
[1, 2, 3] 所以元素的和,def sum(arr):
total = 0
for x in arr:
total += x
return total
def quick_sort(arr):
if len(arr)
def quick_sort(arr):
if len(arr) pivot]
return quick_sort(less) + [pivot] + quick_sort(greater)
def sum(list):
if list = []:
return 0
else:
return list[0] + sum[list[1:]]
def count(list):
if list == []:
return 0
else:
return 1 + count(list[1:])
def max(list):
if len(list) == 2:
return list[0] if list[0] > list[1] else list[1]
sub_max = max(list[1:])
return list[0] if list[0] > sub_max else sub_max
下一篇:python发送邮件