LeetCode 面试题 16.11. 跳水板 | Python
2021-04-23 21:28
标签:交流 ash 组合 返回 tco list 大于 -bash 数学 题目来源:力扣(LeetCode)https://leetcode-cn.com/problems/diving-board-lcci 你正在使用一堆木板建造跳水板。有两种类型的木板,其中长度较短的木板长度为 返回的长度需要从小到大排列。 示例: 提示: 思路:数学 这道题用数学的方法去证明,找规律。先说一下特殊情况: 现在除开上面两种情况,也就是 在这里,我们先将结论给出,然后再去证明。 结论: 跳水板所有长度的结果有 现在来证明如何得到这样的结论: 先假设 观察上面式子,我们知道 因为 那么再结合最开始所述的两个特殊情况,将三者结合起来,就是本题的解。 根据结论,跳水板可能的组合结果如下图: 具体的实现代码如下。 文章原创,欢迎关注点赞。微信公众号《书所集录》同步更新,欢迎关注交流。 LeetCode 面试题 16.11. 跳水板 | Python 标签:交流 ash 组合 返回 tco list 大于 -bash 数学 原文地址:https://www.cnblogs.com/yiluolion/p/13268663.html面试题 16.11. 跳水板
题目
shorter,长度较长的木板长度为 longer。你必须正好使用 k 块木板。编写一个方法,生成跳水板所有可能的长度。输入:
shorter = 1
longer = 2
k = 3
输出: {3,4,5,6}
解题思路
k = 0 的时候,这里表示可使用的木板为 0,那么也就无法建造跳水板,返回空列表 [];shorter == longer 时,那么表示木板长度相同,那么跳水板的长度只有一种可能,那就是 shorter * k。longer > shorter, k > 0 的情况时,会有怎样的结论。k+1 种,而且长度分别为:shorter * k + (longer-shorter) * x, 其中 0 。shorter 的木板有 k-x 个,longer 木板有 x 个。那么跳水板的长度则为: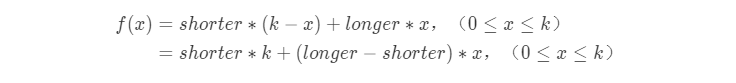
shorter, longer, k 这些都是常量。只有 x 才是变化的。因为 longer > shorter,那么 longer-shorter 一定是大于 0,那么上面的式子就可以看成单调递增的一元一次函数。x 的取值是落在 [0, k] 的(左闭右闭),那么 f(x) 的结果则有 k+1 种(x 从 0 取到 k)。
代码实现
class Solution:
def divingBoard(self, shorter: int, longer: int, k: int) -> List[int]:
# 先处理特殊情况
if k == 0:
return []
if shorter == longer:
return [shorter * k]
# 一般的情况,longer > shorter,k > 0
# 先生成 k+1 长度的数组
ans = [0] * (k+1)
for x in range(k+1):
# 代入公式
ans[x] = shorter * (k - x) + longer * x
return ans
实现结果
总结
[];shorter = longer,木板相等,那么结果只有一个,返回 [shorter * k]。
shorter 木板有 k-x 个,longer 木板有 x 个(其中 0);
f(x)=shorter*(k-x) + longer*x,对公式进行移项,可得:f(x)=shorter*k + (longer-shorter) * x;shorter,longer,k 都是常量,只有 x 的值变化的,而且 longer > shorter,那么上面的式子就可以看出是单调递增的一元一次函数,而 x 的取值落在 [0, k],所以 f(x) 的结果有 k+1 种可能。

文章标题:LeetCode 面试题 16.11. 跳水板 | Python
文章链接:http://soscw.com/index.php/essay/78664.html