十大排序方法
2021-04-25 19:29
阅读:822
排序算法
1. 冒泡排序
- 冒泡排序是一种简单的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
1.1 算法描述
-
n个元素的序列,经过n-1趟选择排序得到有序结果。具体算法描述如下:
- 初始状态:无序区为
R[1..n],有序区为空; - 每一轮从无序区起点开始,相邻元素两两比较,如果前面的比后面的元素大就交换,直到无序区最后。
- 针对所有的元素重复以上的步骤,每一轮冒泡操作无序区域元素减一,有序区元素减一;
- 重复执行
n-1轮,序列变为有序。
1.2 动图演示
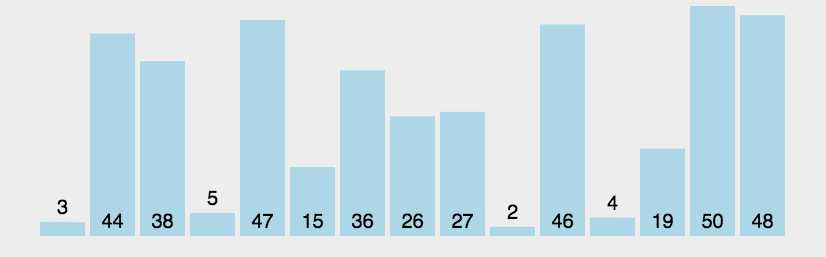
1.3 代码实现
#include
const int maxn=1e4+5,Inf=2147483647;
int a[maxn];
int n;
void Read(){
scanf("%d",&n);
srand(time(0));
for(int i=1;ia[j+1])
std::swap(a[j],a[j+1]);
}
}
void Solve(){
Read();
Bubble_sort(a);
Print();
}
int main(){
Solve();
return 0;
}
2.选择排序
- 选择排序(
Selection-sort)是一种简单直观的排序算法。它的工作原理:首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
2.1 算法描述
-
n个记录的直接选择排序可经过n-1趟直接选择排序得到有序结果。具体算法描述如下:- 初始状态:无序区为
R[1..n],有序区为空; - 第
i趟排序(i=1,2,3…n-1)开始时,当前有序区和无序区分别为R[1..i-1]和R(i..n)。该趟排序从当前无序区中-选出关键字最小的记录R[k],将它与无序区的第1个记录R交换,使R[1..i]和R[i+1..n)分别变为记录个数增加1个的新有序区和记录个数减少1个的新无序区; -
n-1趟结束,数组有序化了。
- 初始状态:无序区为
2.2 动图演示
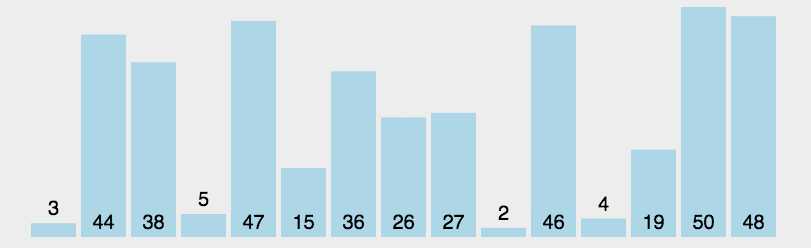
2.3 代码实现
#include
const int maxn=1e4+5,Inf=2147483647;
int a[maxn];
int n;
void Read(){
scanf("%d",&n);
srand(time(0));
for(int i=1;ia[j])
k=j;
std::swap(a[i],a[k]);
}
}
void Solve(){
Read();
Select_sort(a);
Print();
}
int main(){
Solve();
return 0;
}
3. 插入排序
- 插入排序(
Insertion-Sort)的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
3.1 算法描述
- 从第一个元素开始,该元素可以认为已经被排序;
- 取出下一个元素,在已经排序的元素序列中从后向前扫描;
- 如果该元素(已排序)大于新元素,将该元素移到下一位置;
- 重复步骤
3,直到找到已排序的元素小于或者等于新元素的位置; - 将新元素插入到该位置后;
- 重复步骤
2~5。
3.2 动图演示
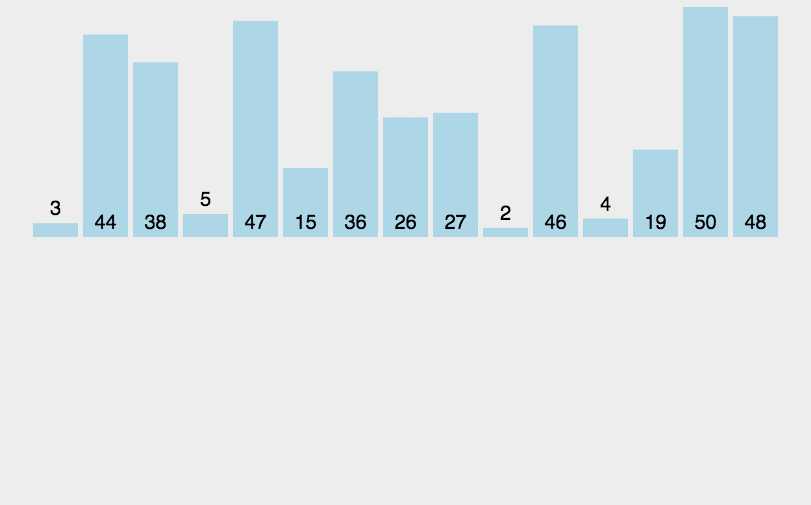
3.3 代码实现
#include
const int maxn=1e4+5,Inf=2147483647;
int a[maxn];
int n;
void Read(){
scanf("%d",&n);
srand(time(0));
for(int i=1;i1 && a[j-1]>a[j];--j)
std::swap(a[j],a[j-1]);
}
}
void Solve(){
Read();
Insert_sort(a);
Print();
}
int main(){
Solve();
return 0;
}
4. Shell排序
-
1959年Shell发明,第一个突破 \(O(n^2)\) 的排序算法,是简单插入排序的改进版。它与插入排序的不同之处在于,它会优先比较距离较远的元素。希尔排序又叫缩小增量排序。
4.1 算法描述
- 选择一个较大的增量,一般选
gap=n/2,把下标为i,i+gap,i+2*gap+...+i+n/gap*gap分为一组,对同组的元素进行插入排序。 - 减小增量为上一个增量的一半,继续操作
1。 - 重复以上操作,直到增量为
1,此时序列变为有序。
4.2 动图演示
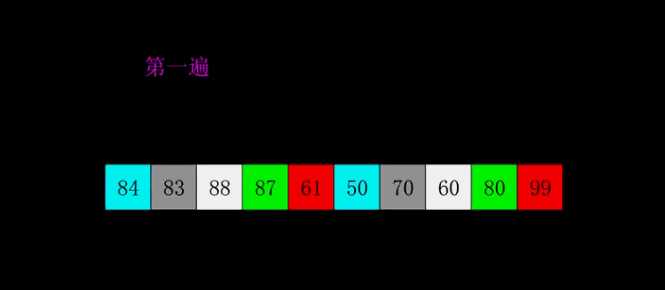
4.3 代码演示
#include
const int maxn=1e4+5,Inf=2147483647;
int a[maxn];
int n;
void Read(){
scanf("%d",&n);
srand(time(0));
for(int i=1;i0;d>>=1){//增量选择,逐渐缩小为原来一半
for(int i=d+1;i0 && a[j] 4.4 时间效率
- 希尔排序中对于增量序列的选择十分重要,直接影响到希尔排序的性能。我们上面选择的增量序列
{n/2,(n/2)/2...1}(希尔增量),其最坏时间复杂度依然为\(O(n^2)\),一些经过优化的增量序列如Hibbard经过复杂证明可使得最坏时间复杂度为\(O(n^{3/2})\)。
5. 归并排序
- 归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(
Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为2-路归并。
5.1 算法描述
- 把长度为n的输入序列分成两个长度为n/2的子序列;
- 对这两个子序列分别采用归并排序;
- 将两个排序好的子序列合并成一个最终的排序序列。
5.2 动图演示
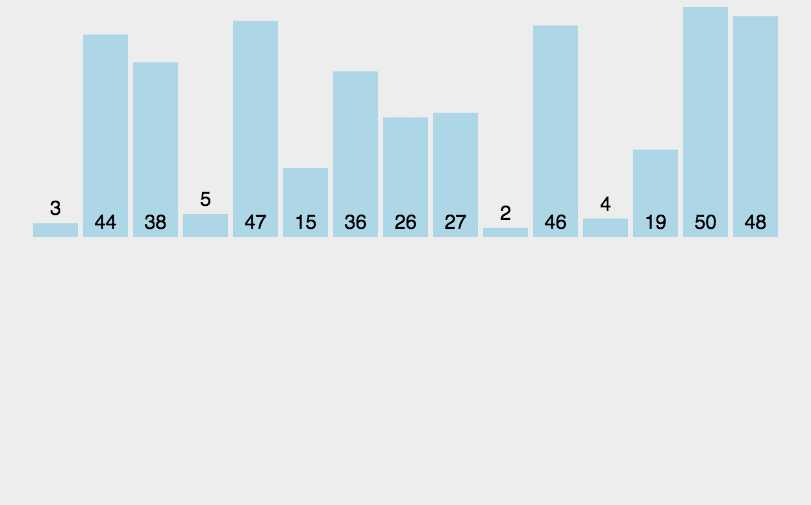
5.3 代码实现
#include
const int maxn=1e4+5,Inf=2147483647;
int a[maxn];
int n;
void Read(){
scanf("%d",&n);
srand(time(0));
for(int i=1;i 5.4 时间效率
- 归并排序是一种稳定的排序方法。和选择排序一样,归并排序的性能不受输入数据的影响,但表现比选择排序好的多,因为始终都是\(O(nlogn)\)的时间复杂度。代价是需要额外的内存空间。
6. 快速排序
- 快速排序的基本思想:通过一趟排序将待排记录分隔成独立的两部分,其中一部分记录的关键字均比另一部分的关键字小,则可分别对这两部分记录继续进行排序,以达到整个序列有序。
6.1 算法描述
- 从数列中挑出一个元素,称为 基准(
pivot); - 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(
partition)操作; - 递归地(
recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
6.2 动图演示
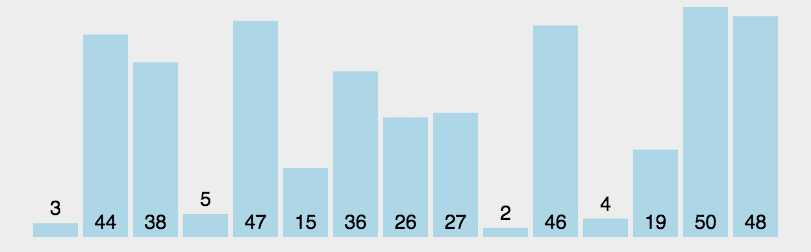
6.3 代码实现
#include
const int maxn=1e4+5,Inf=2147483647;
int a[maxn];
int n;
void Read(){
scanf("%d",&n);
srand(time(0));
for(int i=1;i=r)return;
int i=l,j=r,base=a[l];//选左边界作为基准
while(ibase)--j;//先遍历右边界
while(i 7. 堆排序
- 堆排序 (
Heapsort) 是指利用堆这种数据结构所设计的一种排序算法。 - 堆是一个近似完全二叉树的结构,并同时满足堆的性质:即子结点的键值或索引总是小于(或者大于)它的父结点。
- 堆排序可以说是一种利用堆的概念来排序的选择排序。分为两种方法:
- 大顶堆:每个结点的值都大于或等于其子结点的值,在堆排序算法中用于升序排列;
- 小顶堆:每个结点的值都小于或等于其子结点的值,在堆排序算法中用于降序排列;
- 堆排序的平均时间复杂度为
Ο(nlogn)。
7.1 算法描述:
- 创建一个堆
- 把堆首(最大值)和堆尾互换;
- 堆的大小减一,并向下调整堆使之满足堆的性质
- 重复
2,3直到只剩一个元素。
7.2 动图演示
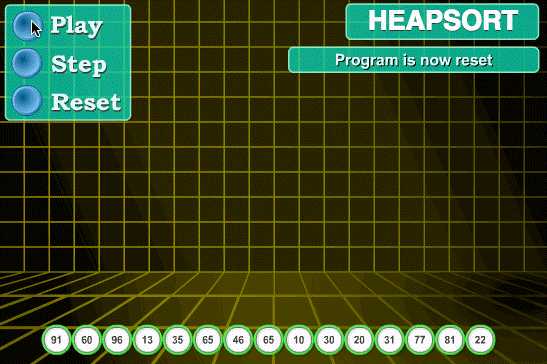
7.3 代码实现
#include
#include
const int maxn = 10000 + 5;
void swap(int &x,int &y){int t=x;x=y;y=t;}//交换函数
int Heap[maxn],siz=0;
void Push(int x){//向上调整
Heap[++siz]=x;//把插入的元素x放在数组最后
for(int i=siz;i/2>0 && Heap[i]>Heap[i/2];i=i/2)
swap(Heap[i],Heap[i/2]);
}
void Pop(){//向下调整
swap(Heap[siz],Heap[1]);siz--;//交换堆顶和堆底,然后直接弹掉堆底
for(int i=1;2*i 8. 计数排序
- 计数排序不是基于比较的排序算法,其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。
8.1 算法描述
- 找出待排序的数组中最大和最小的元素(作为数组的范围);
- 统计数组中每个值为
i的元素出现的次数,存入数组C的第i项; - 对所有的计数累加(从
C中的第一个元素开始,每一项和前一项相加); - 反向填充目标数组:将每个元素i放在新数组的第
C(i)项,每放一个元素就将C(i)减去1。
8.2 动图演示
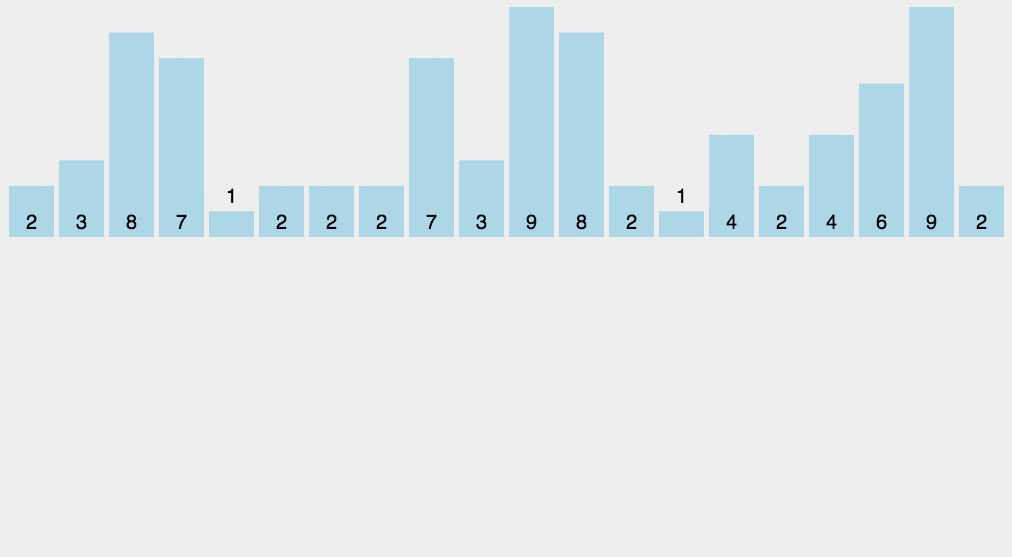
8.3 代码实现
#include
const int maxn=1e5+5,Inf=2147483647;
int n,a[maxn],b[maxn];
void Read(){
scanf("%d",&n);
srand(time(0));
for(int i=1;i 9. 桶排序
- 桶排序是将待排序集合中处于同一个值域的元素存入同一个桶中,也就是根据元素值特性将集合拆分为多个区域,则拆分后形成的多个桶,从值域上看是处于有序状态的。对每个桶中元素进行排序,则所有桶中元素构成的集合是已排序的。
9.1 算法描述
- 设置一个定量的数组当作空桶子。
- 寻访序列,并且把项目一个一个放到对应的桶子去。
- 对每个不是空的桶子进行排序。
- 从不是空的桶子里把项目再放回原来的序列中。
9.2 动图演示
9.3 时间效率
- 桶排序最好情况下使用线性时间
O(n),桶排序的时间复杂度,取决与对各个桶之间数据进行排序的时间复杂度,因为其它部分的时间复杂度都为O(n)。很显然,桶划分的越小,各个桶之间的数据越少,排序所用的时间也会越少。但相应的空间消耗就会增大。
10. 基数排序
- 基数排序是按照低位先排序,然后收集;再按照高位排序,然后再收集;依次类推,直到最高位。有时候有些属性是有优先级顺序的,先按低优先级排序,再按高优先级排序。最后的次序就是高优先级高的在前,高优先级相同的低优先级高的在前。
10.1 算法描述
- 取得数组中的最大数,并取得位数;
-
arr为原始数组,从最低位开始取每个位组成radix数组; - 对
radix进行计数排序(利用计数排序适用于小范围数的特点);
10.2 动图演示

代码实现
#include
const int maxn=1e4+5,Inf=2147483647;
int a[maxn];
int n;
void Read(){
scanf("%d",&n);
srand(time(0));
for(int i=1;i0;--i){// 将数据存储到临时数组b[]中
b[buckets[(a[i]/exp)%10]]=a[i];
buckets[(a[i]/exp)%10]--;
}
for(int i=0;i0;i*=10)// 从个位开始,对数组a按"指数"进行排序
Count_sort(a,n,i);
}
void Solve(){
Read();
Radix_sort(a,n);
Print();
}
int main(){
Solve();
return 0;
}
十大排序方法
标签:时间 quic i+1 inf 赋值 ima string time 遍历
原文地址:https://www.cnblogs.com/hzoi-liujiahui/p/13256439.html
上一篇:基础算法
下一篇:java设计模式面试专题及答案
评论
亲,登录后才可以留言!